点分树学习笔记
一、点分树概述
上文提到,点分治可以处理大规模树上路径问题。但是如果权值带修,点分治就无能为力了。
点分树,又称动态点分治,一般用于解决带修的树上路径相关问题。
温馨提示:
- 权值可以带修,但树的结构不可以,否则就要用到 \(\texttt{LCT}\) 了。
- 一定要分清原树和点分树的区别。
二、点分树建树
点分树的思想很简单,把相邻两层的重心连边,连出来的这棵树就叫做点分树。
比如下面这张图,展示了通过原树是如何构建点分树的:
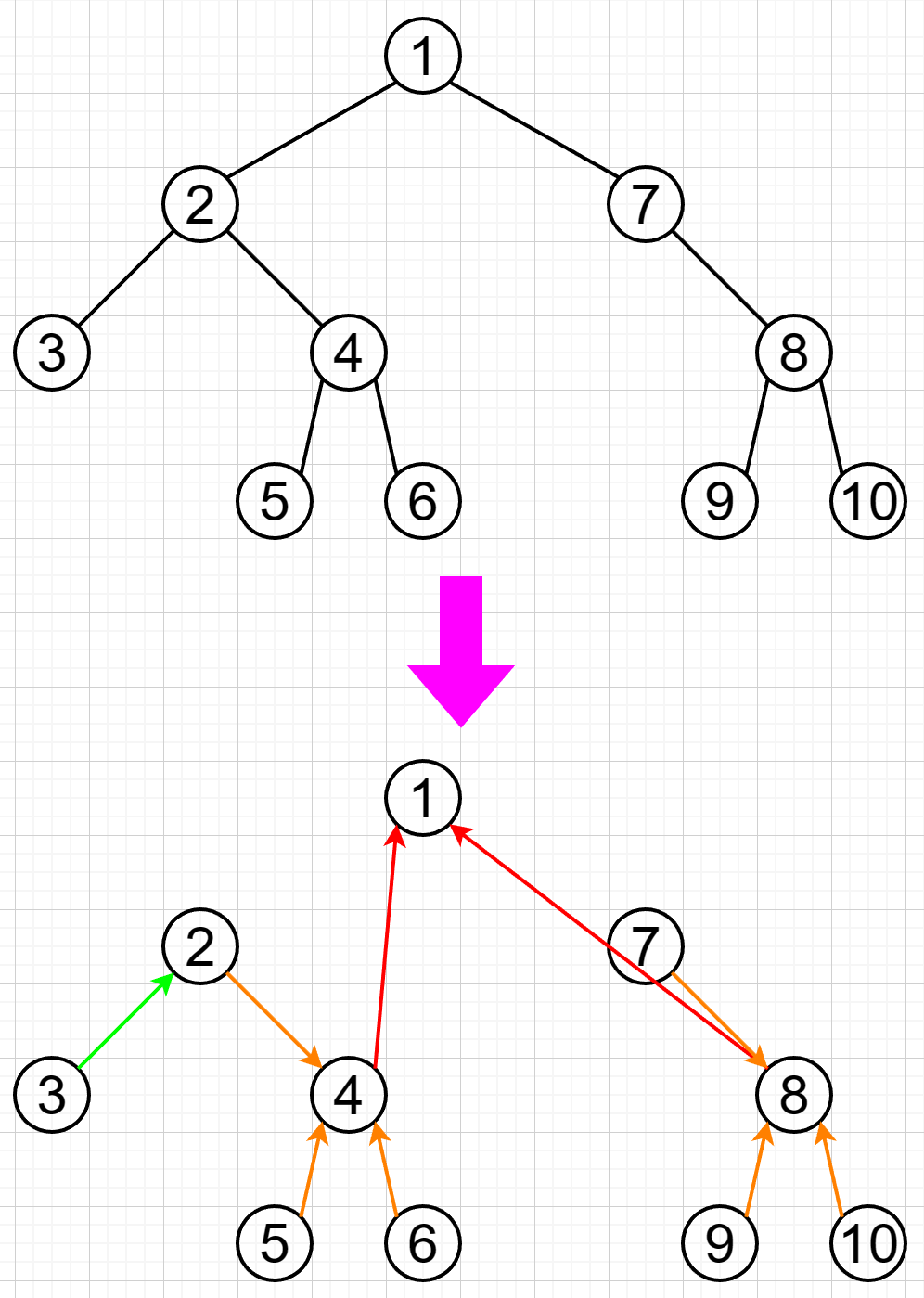
注:第一层边为红边,第二层边为橙边,第三层边为绿边。
代码实现只需要在点分治的 solve 函数中补上连边即可。
void solve(int u)
{
vis[u]=true;
for(auto v:g[u])
{
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),p[rt]=u,solve(rt);
///p[x]为点分树上x的父节点
}
}
注意点分树的根不一定为 \(1\) 号点。
点分树的优美性质:
-
点分树树高为 \(\mathcal O(\log n)\) 。
因此如果需要带修,在点分树上暴力跳 \(fa\) 即可,单次修改的时间复杂度为 \(\mathcal O(\log n)\) 。
-
点分树上每个点的
deg(不算连向父节点的边) \(\le\) 其在原树上的deg。原因很简单, \(u\) 的每个邻点 \(v\) 至多给 \(u\) 在点分树上贡献 \(1\) 个出度。
-
点分树上 \(\sum sz=\mathcal O(n\log n)\) 。
-
点分树上 \(u\) 的子树即为点分治时以 \(u\) 为分治中心的连通块。
-
记点分树上的 \(\texttt{lca}(u,v)=p\),则 \(p\) 一定在原树 \(u\to v\) 的路径上。
常用推论: \(dis_{u,v}=dis_{u,p}+dis_{p,v}\) 。
注意 \(p\) 不一定是原树上 \(u,v\) 两点的 \(\texttt{lca}\) ,但 \(dis_{u,v}\) 表示的是原树上 \(u,v\) 两点的距离。
如果要求 \(dis_{u,v}\) ,仍然需要在原树上倍增或者树剖,这个不是点分树能解决的事情。
博主强烈推荐用树剖,由于树剖很难卡满 \(\log n\) 条重链并且常数很小,实际表现比倍增快大约 \(\frac 13\) ,并且和 \(\mathcal O(1)\) 查询的欧拉序 \(+\ \texttt{ST}\) 表做法差不多。
后面的例题在分析时间复杂度时,默认将求 \(\texttt{lca}\) 的代价视为 \(\mathcal O(1)\) 。
三、点分树相关例题
例1、\(\texttt{P6329 【模板】点分树 | 震波}\)
题目描述
给定一棵 \(n\) 个点的树,点有点权 \(w_i\) 。
接下来 \(m\) 次操作:
0 x k:求到 \(x\) 距离 \(\le k\) 的所有点的点权之和。1 x y:将 \(w_x\) 改为 \(y\) 。
数据范围
- \(1\le n,m\le 10^5\) 。
- \(1\le w_i,y\le 10^4\) ,强制在线。
时间限制 \(\texttt{2s}\) ,空间限制 \(\texttt{250MB}\) 。
分析
先把点分树建出来。
对每个点 \(u\) 开一棵动态开点线段树,保存在点分树上子树中所有点的信息。具体的,对于子树中的每个点 \(x\) ,将 \(w_x\) 的贡献存放在下标为 \(dis_{x,u}\) 的叶子上。
对于修改操作,枚举 \(x\) 在点分树上的祖先 \(u\) ,在线段树上单点修改即可。
对于询问操作,枚举 \(x\) 在点分树上的祖先 \(u\) ,由 \(dis_{x,y}=dis_{x,u}+dis_{u,y}\le k\) ,知 \(dis_{u,y}\le k-dis_{x,u}\) ,线段树求前缀和即可。
本题数据结构需要支持单点修改,求前缀和。
选择写线段树的原因是
从未学过动态开点树状数组。\(\texttt{upd}\) :后来发现树状数组是可以做的,用
vector开数组,以 \(u\) 为根时开到 \(sz_u\) 即可。
但还有一个问题, \(y\) 在 \(u\) 子树中并不代表 \(\texttt{lca}(x,y)=u\) 。
从容斥的角度看,还应该减掉 \(y\) 在 \(u\) 的和 \(x\) 同一方向上的子树中的贡献。
或者换个角度理解,枚举 \(u\) ,减掉 \(u\) 子树中 \(y\) 对 \(p_u\) 的贡献。
对每个点 \(u\) 再开一棵动态开点线段树,将\(w_x\)保存在线段树的第 \(dis_{x,p_u}\) 个叶子上即可。
时间复杂度 \(\mathcal O(n\log^2n)\) 。
来说一下动态开点线段树空间的问题。
乍一看 \(\mathcal O(n\log n)\) 次插入操作,需要 \(\mathcal O(n\log^2n)\) 的空间。
但是取 \(\log n\approx 20\) ,实测开 \(2n\log n\) 个节点就足够了。
下面分析一下原因,对于第 \(x\) 棵线段树,插入的下标均 \(\le sz_x\) 。
因此整棵线段树的结构可以看成上面一条链,下面一个完整的,点数为 \(sz_x\) 的线段树,总节点数 \(\le 4\cdot sz_x+\log n\) 。
由于 \(\sum sz_x\le n\log n\) ,因此总节点数 \(\le 5n\log n\) 。
不过实际情况下很难卡满(而且上面的估计略显粗略),本题开到 \(2n\log n\) 的空间就足够了。
如果你不想动脑子来算空间复杂度,也可以直接把数组开大一点,
比较省事。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int m,n,u,v,op,rt,all,res;
int d[maxn],fa[maxn],son[maxn],top[maxn];
int p[maxn],mx[maxn],sz[maxn];///注意sz在树剖和点分治找重心时都用到了,但含义不同
bool vis[maxn];
vector<int> g[maxn];
int w[maxn];
struct sgmt
{
int tot,rt[maxn];
struct node
{
int ls,rs,sum;
}f[40*maxn];
void pushup(int p)
{
f[p].sum=f[f[p].ls].sum+f[f[p].rs].sum;
}
void modify(int &p,int l,int r,int pos,int val)
{
if(!p) p=++tot;
if(l==r) return f[p].sum+=val,void();
int mid=(l+r)/2;
if(pos<=mid) modify(f[p].ls,l,mid,pos,val);
else modify(f[p].rs,mid+1,r,pos,val);
pushup(p);
}
int query(int p,int l,int r,int L,int R)
{
if(L<=l&&r<=R) return f[p].sum;
if(!p||l>R||r<L) return 0;
int mid=(l+r)/2;
return query(f[p].ls,l,mid,L,R)+query(f[p].rs,mid+1,r,L,R);
}
}t1,t2;
void dfs1(int u,int father)
{
sz[u]=1;
for(auto v:g[u])
{
if(v==father) continue;
d[v]=d[u]+1,fa[v]=u;
dfs1(v,u),sz[u]+=sz[v];
if(sz[v]>=sz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int topf)
{
top[u]=topf;
if(son[u]) dfs2(son[u],topf);
for(auto v:g[u])
{
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
int lca(int u,int v)
{
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
u=fa[top[u]];
}
return d[u]<d[v]?u:v;
}
int getdis(int u,int v)
{
return d[u]+d[v]-2*d[lca(u,v)];
}
void getroot(int u,int fa)
{
sz[u]=1,mx[u]=0;
for(auto v:g[u])
{
if(vis[v]||v==fa) continue;
getroot(v,u);
sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
}
mx[u]=max(mx[u],all-sz[u]);
if(mx[u]<mx[rt]) rt=u;
}
void solve(int u)
{
vis[u]=true;
for(auto v:g[u])
{
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),p[rt]=u,solve(rt);
}
}
void modify(int x,int y)
{
for(int cur=x;cur;cur=p[cur])
{
t1.modify(t1.rt[cur],0,n,getdis(x,cur),y);
if(p[cur]) t2.modify(t2.rt[cur],0,n,getdis(x,p[cur]),y);
}
}
int query(int x,int k)
{
int res=0;
for(int cur=x;cur;cur=p[cur])
{
res+=t1.query(t1.rt[cur],0,n,0,k-getdis(x,cur));
if(p[cur]) res-=t2.query(t2.rt[cur],0,n,0,k-getdis(x,p[cur]));
}
return res;
}
int main()
{
scanf("%d%d",&n,&m),mx[0]=1e9;
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d",&u,&v);
g[u].push_back(v),g[v].push_back(u);
}
d[1]=1,dfs1(1,0),dfs2(1,1);
all=n,getroot(1,0),solve(rt);
for(int i=1;i<=n;i++) modify(i,w[i]);
while(m--)
{
scanf("%d%d%d",&op,&u,&v),u^=res,v^=res;
if(!op) printf("%d\n",res=query(u,v));
else modify(u,v-w[u]),w[u]=v;
}
return 0;
}
例2、\(\texttt{P2056 [ZJOI2007] 捉迷藏}\)
题目描述
给定一棵 \(n\) 个点的树,每个点有黑白两种颜色,初始全为黑色。
接下来 \(q\) 次操作:
C i:改变第 \(i\) 个点的颜色。G:查询最远的两个黑点的距离。如果没有黑点,输出-1;如果只有一个黑点,输出0。
数据范围
- \(1\le n\le 10^5,1\le q\le 5\cdot 10^5\) 。
时间限制 \(\texttt{5s}\) ,空间限制 \(\texttt{250MB}\) 。
分析
还是先建出点分树。我们希望对每个点 \(u\) ,维护以 \(u\) 为(点分树上) \(\texttt{lca}\) 的最远黑色点对的距离。
用一个数据结构(记为 A ),维护 \(u\) 子树内的所有黑点到 \(p_u\) 的距离。
再用一个数据结构(记为 B ),维护对 \(u\) 的每个子节点 \(v\) ,A[v] 中的最大值。注意如果 \(u\) 是黑点,还要在 B[u] 中 push 一个 0 ,表示 \(u\) 对自己的贡献。
至此,我们已经可以维护以 \(u\) 为 \(\texttt{lca}\) 的最远黑色点对距离了,即 B[u] 中最大值和次大值之和。
最后还需要一个数据结构(记为 C ),维护对每个 \(u\) , B[u] 中最大值和次大值之和。
修改比较简单,顺着链往上跳即可。
那么 A,B,C 应该选用什么数据结构呢?
我们需要支持插入、删除、求最大值和次大值的操作,可以用平衡树解决。
但是为了减小常数,最好的选择是可删堆。
可删堆的原理:
q1维护已经插入堆中的元素,q2维护懒惰删除的元素,如果q1和q2的堆顶相同,将这个元素同时从q1和q2中删除。
时间复杂度 \(\mathcal O((n+q)\log^2n)\) 。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5,inf=1e9;
int n,q,u,v,rt,all,sum;
int d[maxn],fa[maxn],son[maxn],top[maxn];
int p[maxn],mx[maxn],sz[maxn];
bool vis[maxn];
vector<int> g[maxn];
int w[maxn];
char ch[2];
struct pq
{
priority_queue<int> q1,q2;
void clean()
{
while(q1.size()&&q2.size()&&q1.top()==q2.top()) q1.pop(),q2.pop();
}
int size()
{
return q1.size()-q2.size();
}
void push(int x)
{
q1.push(x),clean();
}
void del(int x)
{
q2.push(x),clean();
}
int top()
{
return q1.size()?q1.top():-inf;
}
int query()
{
static int x,y;
x=top(),del(x),y=top(),push(x);
return x+y;
}
}a[maxn],b[maxn],c;
void dfs1(int u,int father)
{
sz[u]=1;
for(auto v:g[u])
{
if(v==father) continue;
d[v]=d[u]+1,fa[v]=u;
dfs1(v,u),sz[u]+=sz[v];
if(sz[v]>=sz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int topf)
{
top[u]=topf;
if(son[u]) dfs2(son[u],topf);
for(auto v:g[u])
{
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
int lca(int u,int v)
{
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
u=fa[top[u]];
}
return d[u]<d[v]?u:v;
}
int getdis(int u,int v)
{
return d[u]+d[v]-2*d[lca(u,v)];
}
void getroot(int u,int fa)
{
sz[u]=1,mx[u]=0;
for(auto v:g[u])
{
if(vis[v]||v==fa) continue;
getroot(v,u);
sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
}
mx[u]=max(mx[u],all-sz[u]);
if(mx[u]<mx[rt]) rt=u;
}
void solve(int u)
{
vis[u]=true;
for(auto v:g[u])
{
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),p[rt]=u,solve(rt);
}
}
void add(int x)
{
c.del(b[x].query());
b[x].push(0);
c.push(b[x].query());
for(int i=x;p[i];i=p[i])
{
c.del(b[p[i]].query());
b[p[i]].del(a[i].top());
a[i].push(getdis(x,p[i]));
b[p[i]].push(a[i].top());
c.push(b[p[i]].query());
}
}
void del(int x)
{
c.del(b[x].query());
b[x].del(0);
c.push(b[x].query());
for(int i=x;p[i];i=p[i])
{
c.del(b[p[i]].query());
b[p[i]].del(a[i].top());
a[i].del(getdis(x,p[i]));
b[p[i]].push(a[i].top());
c.push(b[p[i]].query());
}
}
int main()
{
scanf("%d",&n),mx[0]=inf;
for(int i=1;i<=n-1;i++)
{
scanf("%d%d",&u,&v);
g[u].push_back(v),g[v].push_back(u);
}
d[1]=1,dfs1(1,0),dfs2(1,1);
all=n,getroot(1,0),solve(rt);
for(int x=1;x<=n;x++)
{
w[x]=1,b[x].push(0);
for(int i=x;i;i=p[i]) a[i].push(getdis(x,p[i]));
}
for(int i=1;i<=n;i++) b[p[i]].push(a[i].top());
for(int i=1;i<=n;i++) c.push(b[i].query());
scanf("%d",&q),sum=n;
while(q--)
{
scanf("%s",ch);
if(ch[0]=='C')
{
scanf("%d",&u),sum+=w[u]?-1:1,w[u]^=1;
w[u]?add(u):del(u);
}
else printf("%d\n",sum>=2?c.top():sum-1);
}
return 0;
}
例3、\(\texttt{P3345 [ZJOI2015]幻想乡战略游戏}\)
题目描述
给定一棵 \(n\) 个节点的树,点有点权 \(d_u\) (初始全为零),边有边权 \(w_i\) 。
接下来 \(q\) 次操作,每次操作 u e 表示给 \(d_u\) 加上 \(e\) ,保证任意时刻 \(d_u\) 非负。
在每次操作结束后,求 \(\min\limits_{1\le u\le n}\sum_{v=1}^nd_v\cdot dis(u,v)\) 。
保证每个点的度数 \(\le 20\) 。
数据范围
- \(1\le n,q\le 10^5\) 。
- \(0\le w_i,|e|\le10^3\) 。
时间限制 \(\texttt{6s}\) ,空间限制 \(\texttt{250MB}\) 。
分析
点分治重心移动的套路又出现了!推荐一篇比较清晰的题解。
本题相当于动态维护带权重心。
先考虑根节点从 \(u\) 移动到邻点 \(v\) 时,带权距离和的变化。
以 \(u\) 为根,记 \(s_v\) 为 \(v\) 子树的点权和,则带权距离和的变化量为:
当 \(2\cdot s_v>s_u\) 时,带权距离和会变小,并且这样的 \(v\) 至多只有一个。
如果这样的 \(v\) 不存在,则说明 \(u\) 就是重心。
如果树退化成一条链,则移动次数可以卡满 \(\mathcal O(n)\) 。
但如果每次跳到点分治时 \(v\) 所在连通块的重心,则移动次数为 \(\mathcal O(\log n)\) 。
划重点:对于点分树上的一条边 \(u\to v\) ,如果 \((u,w)\) 是原树上的边,满足 \(w\) 在点分树上 \(v\) 子树中。那么判断是否移动用的是 \(u\) 和 \(w\) 比较,如果需要移动,则移动到 \(v\) 。
如果每次只移动一步,则带权路径和逐渐变小,满足单调性。
但对于 \(u\to v\) 这种移动,相当于在原树上移动了很多条边,不满足单调性。换句话说,以 \(v\) 为根的带权路径和不一定比 \(u\) 更优。
通过 \(2\cdot s_v\gt s_u\) 进行判断并不方便(需要树状数组维护子树点权和),直接求出以 \(u\) 和 \(v\) 为根时的答案然后进行比较即可。
最后一个问题,固定根节点 \(u\) ,求带权距离和。
其实这一部分仅仅是个点分树板子,是复杂度瓶颈但不是难点。
枚举点分树上 \(u\) 的祖先 \(x\) ,希望统计满足 \(\texttt{lca}(u,v)=x\) 的所有 \(v\) 的贡献。
注意到 \(d_v\cdot dis_{u,v}=d_v\cdot(dis_{u,cur}+dis_{cur,v})\) ,因此我们需要对每个点 \(x\) ,维护点分树上子树的 \(\sum d_v\) 和 \(\sum d_v\cdot dis_{x,v}\) 。
由于需要容斥和 \(u\) 在 \(x\) 的同一子树的贡献,额外维护 \(\sum d_v\cdot dis_{p_{x},v}\) 即可。
时间复杂度 \(\mathcal O(qd\log n+q\log^2n)\) ,其中 \(d=20\) 为最大度数。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=1e5+5;
int n,q,u,v,w,x,rt,all;
int c[maxn],d[maxn],fa[maxn],sz[maxn],son[maxn],top[maxn];
int p[maxn],mx[maxn];
bool vis[maxn];
vector<pii> g[maxn],h[maxn];
ll s1[maxn],s2[maxn],s3[maxn];
void dfs1(int u,int f)
{
sz[u]=1;
for(auto [v,w]:g[u])
{
if(v==f) continue;
c[v]=c[u]+w,d[v]=d[u]+1,fa[v]=u,dfs1(v,u),sz[u]+=sz[v];
if(sz[v]>=sz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int f)
{
top[u]=f;
if(son[u]) dfs2(son[u],f);
for(auto [v,w]:g[u])
{
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
int lca(int u,int v)
{
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
u=fa[top[u]];
}
return d[u]<d[v]?u:v;
}
int getdis(int u,int v)
{
return c[u]+c[v]-2*c[lca(u,v)];
}
void getroot(int u,int fa)
{
sz[u]=1,mx[u]=0;
for(auto [v,w]:g[u])
{
if(vis[v]||v==fa) continue;
getroot(v,u),sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
}
mx[u]=max(mx[u],all-sz[u]);
if(!rt||mx[u]<mx[rt]) rt=u;
}
void solve(int u)
{
vis[u]=1;
for(auto [v,w]:g[u])
{
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),p[rt]=u,h[u].push_back(mp(v,rt)),solve(rt);
}
}
void modify(int u,int e)
{
for(int i=u;i;i=p[i])
{
s1[i]+=e,s2[i]+=1ll*getdis(u,i)*e;
if(p[i]) s3[i]+=1ll*getdis(u,p[i])*e;
}
}
ll calc(int u)
{
ll res=0;
for(int i=u;i;i=p[i])
{
res+=s1[i]*getdis(u,i)+s2[i];
if(p[i]) res-=s1[i]*getdis(u,p[i])+s3[i];
}
return res;
}
ll query(int u)
{
ll res=calc(u);
for(auto [v,w]:h[u]) if(calc(v)<res) return query(w);
return res;
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d%d",&u,&v,&w);
g[u].push_back(mp(v,w)),g[v].push_back(mp(u,w));
}
d[1]=1,dfs1(1,0),dfs2(1,1);
all=n,getroot(1,0),solve(x=rt);
while(q--) scanf("%d%d",&u,&w),modify(u,w),printf("%lld\n",query(x));
return 0;
}
例4、\(\texttt{P3676 小清新数据结构题}\)
题目描述
给定一棵 \(n\) 个点的树,点有点权 \(w_i\) 。
接下来 \(q\) 次操作:
1 x y:将第 \(x\) 个点的点权改为 \(y\) 。2 x:查询以 \(x\) 为根时,每棵子树点权和的平方之和。
数据范围
- \(1\le n,q\le 2\cdot 10^5\)
- \(1\le x\le n,0\le |w_i|,|y|\le 10\) 。
时间限制 \(\texttt{2s}\) ,空间限制 \(\texttt{256MB}\) 。
分析
本题最简洁的做法不是点分树,而是树剖树状数组。
推式子,先任意指定根节点 \(p\) 。
记 \(sum=\sum_{i=1}^nw_i,s_i=\sum\limits_{j\in subtree(i)}w_j\) ,目标计算 \(\sum_{i=1}^ns_i^2\) 。
平方和不好维护,先计算 \(\sum_{i=1}^ns_i\) 。
这个直接拆成每个点的贡献来算:
其中 \(\sum_{i=1}^nw_i\cdot dis_{i,p}\) 用上一道题的方法可以快速维护。
接下来需要一个常用二级结论:\(S=\sum_{i=1}^ns_i\cdot(sum-s_i)\)与 \(p\) 无关!
原因也很简单,每条边的贡献是两端连通块点权乘积之和的两倍。
但是这个结论可以用来降次:
最后一个问题是如何快速维护 \(S\) 。
拆成边的贡献依然不好算,我们把贡献拆到所有点对上:
所以对于修改操作,\(S\)的增量为:
直接交给点分树来计算即可。
时间复杂度 \(\mathcal O((n+q)\log n)\) 。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2e5+5;
int n,q,u,v,op,rt,all;
ll cur,sum;
int d[maxn],fa[maxn],son[maxn],top[maxn];
int p[maxn],mx[maxn],sz[maxn];
bool vis[maxn];
vector<int> g[maxn];
int w[maxn];
ll s[maxn],s1[maxn],s2[maxn],s3[maxn];
void dfs1(int u,int father)
{
sz[u]=1,s[u]=w[u];
for(auto v:g[u])
{
if(v==father) continue;
d[v]=d[u]+1,fa[v]=u;
dfs1(v,u),sz[u]+=sz[v],s[u]+=s[v];
if(sz[v]>=sz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int topf)
{
top[u]=topf;
if(son[u]) dfs2(son[u],topf);
for(auto v:g[u])
{
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
int lca(int u,int v)
{
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
u=fa[top[u]];
}
return d[u]<d[v]?u:v;
}
int getdis(int u,int v)
{
return d[u]+d[v]-2*d[lca(u,v)];
}
void getroot(int u,int fa)
{
sz[u]=1,mx[u]=0;
for(auto v:g[u])
{
if(vis[v]||v==fa) continue;
getroot(v,u);
sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
}
mx[u]=max(mx[u],all-sz[u]);
if(mx[u]<mx[rt]) rt=u;
}
void solve(int u)
{
vis[u]=true;
for(auto v:g[u])
{
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),p[rt]=u,solve(rt);
}
}
ll calc(int x)
{
ll res=0;
for(int i=x;i;i=p[i])
{
res+=s1[i]*getdis(x,i)+s2[i];
if(p[i]) res-=s1[i]*getdis(x,p[i])+s3[i];
}
return res;
}
void modify(int x,int y)
{
sum+=y,cur+=y*calc(x);
for(int i=x;i;i=p[i])
{
s1[i]+=y,s2[i]+=y*getdis(x,i);
if(p[i]) s3[i]+=y*getdis(x,p[i]);
}
}
int main()
{
scanf("%d%d",&n,&q),mx[0]=1e9;
for(int i=1;i<=n-1;i++)
{
scanf("%d%d",&u,&v);
g[u].push_back(v),g[v].push_back(u);
}
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
d[1]=1,dfs1(1,0),dfs2(1,1);
all=n,getroot(1,0),solve(rt);
sum=s[1];
for(int x=1;x<=n;x++)
{
cur+=s[x]*(sum-s[x]);
for(int i=x;i;i=p[i])
{
s1[i]+=w[x],s2[i]+=w[x]*getdis(x,i);
if(p[i]) s3[i]+=w[x]*getdis(x,p[i]);
}
}
while(q--)
{
scanf("%d",&op);
if(op==1) scanf("%d%d",&u,&v),modify(u,v-w[u]),w[u]=v;
else scanf("%d",&u),printf("%lld\n",sum*(calc(u)+sum)-cur);
}
return 0;
}
例5、\(\texttt{P3241 [HNOI2015]开店}\)
题目描述
给定一棵 \(n\) 个点的树,点有点权 \(x_i\) ,边有边权 \(w_i\) 。
\(q\) 次询问,每次给定 \(u,l,r\) ,求 \(\sum\limits_{l\le x_i\le r}dis_{u,i}\) ,强制在线。
数据范围
- \(1\le n\le 1.5\cdot 10^5,q\le 2\cdot 10^5\) 。
- \(0\le x_i\lt 10^9,1\le w_i\le10^3\) 。
时间限制 \(\texttt{6s}\) ,空间限制 \(\texttt{500MB}\) 。
分析
根据模板题的套路,枚举 \(u\) 在点分树上的祖先 \(x\) ,统计 \(\sum\limits_{l\le x_v\le r,lca(u,v)=x}dis_{u,v}\) 。
把 \(dis_{u,v}\) 拆成 \(dis_{u,x}+dis_{x,v}\),对每个 \(x\) 用 vector 存储二元组 \((y,dis_{x,y})\) 或 \((x,dis_{p_x,y})\) ,查询时直接用 \(l\) 和 \(r\) 二分即可。
时间复杂度 \(\mathcal O((n+q)\log^2n)\) 。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1.5e5+5,maxm=3e5+5;
int l,n,q,r,u,v,w,rt,all,lim,tot=1;
ll res;
int head[maxn],to[maxm],val[maxm],nxt[maxm];
int x[maxn];
int d[maxn],fa[maxn],dis[maxn],son[maxn],top[maxn];
int p[maxn],mx[maxn],sz[maxn];
bool vis[maxn];
struct node
{
int x;
ll dis[2];
};
bool operator<(const node &a,const node &b)
{
return a.x<b.x;
}
struct vec
{
vector<node> h;
void init()
{
sort(h.begin()+1,h.end());
for(int i=1;i<h.size();i++)
for(int j=0;j<=1;j++)
h[i].dis[j]+=h[i-1].dis[j];
}
ll query(int op,int l,int r)
{
l=lower_bound(h.begin()+1,h.end(),(node){l,0,0})-h.begin();
r=upper_bound(h.begin()+1,h.end(),(node){r,0,0})-h.begin()-1;
if(op==-1) return r-l+1;
else return h[r].dis[op]-h[l-1].dis[op];
}
}t[maxn];
void addedge(int u,int v,int w)
{
nxt[++tot]=head[u],to[tot]=v,val[tot]=w,head[u]=tot;
}
void dfs1(int u,int father)
{
sz[u]=1;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i],w=val[i];
if(v==father) continue;
d[v]=d[u]+1,dis[v]=dis[u]+w,fa[v]=u;
dfs1(v,u),sz[u]+=sz[v];
if(sz[v]>=sz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int topf)
{
top[u]=topf;
if(son[u]) dfs2(son[u],topf);
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
int lca(int u,int v)
{
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
u=fa[top[u]];
}
return d[u]<d[v]?u:v;
}
int getdis(int u,int v)
{
return dis[u]+dis[v]-2*dis[lca(u,v)];
}
void getroot(int u,int fa)
{
sz[u]=1,mx[u]=0;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(vis[v]||v==fa) continue;
getroot(v,u);
sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
}
mx[u]=max(mx[u],all-sz[u]);
if(mx[u]<mx[rt]) rt=u;
}
void solve(int u)
{
vis[u]=true;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),p[rt]=u,solve(rt);
}
}
int main()
{
scanf("%d%d%d",&n,&q,&lim),mx[0]=1e9;
for(int i=1;i<=n;i++) scanf("%d",&x[i]);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d%d",&u,&v,&w);
addedge(u,v,w),addedge(v,u,w);
}
d[1]=1,dfs1(1,0),dfs2(1,1);
all=n,getroot(1,0),solve(rt);
for(int i=1;i<=n;i++) t[i].h.push_back({0,0,0});
for(int u=1;u<=n;u++)
for(int i=u;i;i=p[i])
t[i].h.push_back({x[u],getdis(u,i),getdis(u,p[i])});
for(int i=1;i<=n;i++) t[i].init();
while(q--)
{
scanf("%d%d%d",&u,&l,&r),l=(l+res)%lim,r=(r+res)%lim,res=0;
if(l>r) swap(l,r);
for(int i=u;i;i=p[i])
{
ll cnt=t[i].query(-1,l,r);
res+=cnt*getdis(u,i)+t[i].query(0,l,r);
if(p[i]) res-=cnt*getdis(u,p[i])+t[i].query(1,l,r);
}
printf("%lld\n",res);
}
return 0;
}
例6、\(\texttt{P5311 [Ynoi2011] 成都七中}\)
题目描述
给定一棵 \(n\) 个节点的树,点有颜色 \(c_i\) 。
\(m\) 次查询保留编号在 \([l,r]\) 内的所有节点, \(x\) 所在连通块的颜色种类数。
查询操作相互独立。
数据范围
- \(1\le n,m,c_i\le 10^5\) 。
- \(1\le l\le x\le r\le n\) 。
时间限制 \(\texttt{1s}\) ,空间限制 \(\texttt{250MB}\) 。
分析
考虑 \(x\) 所在的连通块在点分治过程中的变化。
原本这个连通块是完整的,直到某个分治中心刚好落在连通块中,然后这个连通块就 "散架" 了。
我们要做的第一件事情就是找到这个分治中心 \(u\) ,枚举 \(x\) 在点分树上的祖先 \(u\) ,最浅的满足 \(u\to x\) 路径上所有点都在 \([l,r]\) 内的 \(u\) 即为所求。
再来考虑怎么计算贡献。
由于连通块中任意两点连通,所以 \(x\) 不再重要,可以将询问挂在 \(u\) 上。
对 \(u\) 子树中的每个点 \(y\) ,用二元组 \((L,R)\) 表示,其中 \(L,R\) 分别为 \(u\to y\) 路径上的最小、最大节点编号。
我们要统计 \(l\le L,R\le r\) (即 \((l,r)\) 右下角)不同颜色数量。
对横坐标从右往左扫描线,记录每种颜色出现的最小纵坐标,并将相应位置设成 \(1\) ,询问用树状数组求前缀和即可。
时间复杂度 \(\mathcal O((n+m)\log^2n)\) 。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5,lim=1e5,inf=1e9;
int l,m,n,r,u,v,rt,all;
int mx[maxn],sz[maxn];
int c[maxn],col[maxn],pos[maxn],res[maxn];
bool vis[maxn];
vector<int> g[maxn];
struct node
{
int l,r,id;
};
vector<node> h[maxn];
struct oper
{
int l,r,x,op;
///op=0,在(l,r)位置插入颜色为x的点
///op=1,询问(l,r)右下角颜色数,编号为x
};
vector<oper> vec[maxn];
bool cmp(oper a,oper b)
{
if(a.l!=b.l) return a.l>b.l;
return a.op<b.op;
}
void getroot(int u,int fa)
{
sz[u]=1,mx[u]=0;
for(auto v:g[u])
{
if(vis[v]||v==fa) continue;
getroot(v,u);
sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
}
mx[u]=max(mx[u],all-sz[u]);
if(mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa,int l,int r,int rt)
{
h[u].push_back({l,r,rt});
vec[rt].push_back({l,r,col[u],0});
for(auto v:g[u])
{
if(vis[v]||v==fa) continue;
dfs(v,u,min(l,v),max(r,v),rt);
}
}
void solve(int u)
{
vis[u]=true,dfs(u,0,u,u,u);
for(auto v:g[u])
{
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),solve(rt);
}
}
void add(int x,int v)
{
while(x<=lim) c[x]+=v,x+=x&(-x);
}
int sum(int x)
{
int res=0;
while(x) res+=c[x],x-=x&(-x);
return res;
}
int main()
{
scanf("%d%d",&n,&m),mx[0]=inf;
for(int i=1;i<=n;i++) scanf("%d",&col[i]);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d",&u,&v);
g[u].push_back(v),g[v].push_back(u);
}
all=n,getroot(1,0),solve(rt);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&l,&r,&u);
for(auto p:h[u])
if(l<=p.l&&p.r<=r)
{
rt=p.id;
break;
}
vec[rt].push_back({l,r,i,1});
}
for(int i=1;i<=lim;i++) pos[i]=inf;
for(int i=1;i<=n;i++)
{
sort(vec[i].begin(),vec[i].end(),cmp);
for(auto p:vec[i])
{
if(!p.op)
{
if(p.r>=pos[p.x]) continue;
add(pos[p.x],-1),add(p.r,1),pos[p.x]=p.r;
}
else res[p.x]=sum(p.r);
}
for(auto p:vec[i]) if(!p.op) add(pos[p.x],-1),pos[p.x]=inf;
}
for(int i=1;i<=m;i++) printf("%d\n",res[i]);
return 0;
}
本文来自博客园,作者:peiwenjun,转载请注明原文链接:https://www.cnblogs.com/peiwenjun/p/18711855


 浙公网安备 33010602011771号
浙公网安备 33010602011771号