CF1257G Divisor Set 题解

题目描述

给定 \(n\) 个质数 \(p_1,\cdots,p_n\) ，记 \(m=\prod_{i=1}^np_i\) 。

求最大的由 \(m\) 的因数构成的集合 \(S\) ，满足 \(\forall x,y\in S,x\neq y\) ，均有 \(x\not\mid y\) 。

输出 \(|S|\bmod 998244353\) 。

数据范围

• \(1\le n\le 2\cdot 10^5\) 。
• \(2\le p_i\le 3\cdot 10^6\) ，保证 \(p_i\) 为质数。

时间限制 \(\texttt{5s}\) ，空间限制 \(\texttt{512MB}\) 。

分析

记 \(deg(x)\) 为 \(x\) 的质因子个数，比如 \(deg(12)=3\) 。

由题 \(deg(m)=n\) 。容易想到取 \(S=\{x|deg(x)=\lfloor\frac n2\rfloor\}\) ，但如何证明此时 \(|S|\) 最大？

证明

当 \(m\) 为 \(\texttt{square free}\) 时，问题退化为 \(\texttt{Sperner}\) 定理。

\(\texttt{Sperner}\) 定理：对于 \(|S|=n\) ，记 \(\mathcal F\) 为 \(S\) 的子集族，若 \(A_1,\cdots,A_k\subset\mathcal F\) 且没有包含关系，则 \(k\le\binom n{\lfloor\frac n2\rfloor}\) 。

证明：

对 \(\forall A_i\) ，将 \(A_i\) 中所有元素全排列写在前面，将 \(\overline{A_i}\) 中所有元素全排列写在后面，显然一个 \(A_i\) 会对应 \(S\) 的 \(\big(|A_i|\big)!\big(n-|A_i|\big)!\) 个排列。

由 \(A_i\) 两两不交，知这些排列不会重复，因此：

\[n!\ge\sum_{i=1}^k\big(|A_i|\big)!\big(n-|A_i|\big)! \]

两边同时除以 \(n!\) ：

\[1\ge\sum_{i=1}^k\frac 1{\binom n{|A_i|}}\ge k\cdot\frac 1{\binom n{\lfloor\frac n2\rfloor}}\\ \]

证毕。

根据 \(\texttt{Dilworth}\) 定理，最小链覆盖等于最长反链，我们只需要将 \(m\) 的所有因数划分成 \(\binom n{\lfloor\frac n2\rfloor}\) 条链。

考虑数学归纳法，假设命题对 \(m\) 成立，只需证明命题对 \(m\cdot p^\lambda\) 也成立。

先给出对称链的定义。若由 \(m\) 的因数构成的数列 \(d_1,\cdots,d_h\) 满足如下性质：

• \(deg(d_1)=deg(\frac m{d_h})\) ，换言之 \(deg(d_1)+deg(d_h)=deg(m)\) 。
• \(\forall 1\le i\lt h,\frac{d_{i+1}}{d_i}\in\texttt{prime}\) 。

则称 \(d_1,\cdots,d_h\) 为 \(m\) 的一条对称链。

对于 \(m\) 的任意一条对称链 \(d_1,\cdots,d_h\) ，只需将 \(d_i\cdot p^j\) 划分成若干条 \(m\cdot p^\lambda\) 的对称链，归纳就完成了。

• 第一条： \(d_1,\cdots,d_1\cdot p^\lambda,\cdots,d_h\cdot p^\lambda\) 。
• 第二条： \(d_2,\cdots,d_2\cdot p^{\lambda-1},\cdots,d_h\cdot p^{\lambda-1}\) 。
• 依次类推，直到铺满整个矩形。

这里盗用一张图，每个 \(\texttt{L}\) 字形区域为一条对称链：

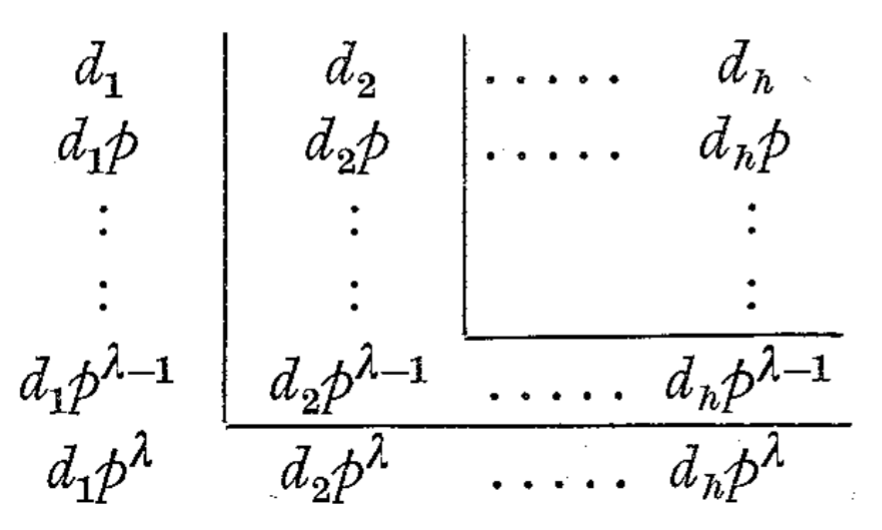
由 \(deg(d_1)+deg(d_h)=deg(m)\) （对称链定义）知， \(deg(d_1)+deg(d_h\cdot p^\lambda)=deg(m\cdot p^\lambda)\) ，即第一条链为 \(m\cdot p^\lambda\) 的对称链。

后面每条链在上一条链的基础上，开头 \(deg\) 加一，结尾 \(deg\) 减一，因此每条链都是 \(m\cdot p^\lambda\) 的对称链，证毕。

分治 NTT

设 \(m=p_1^{\alpha_1}\cdots p_k^{\alpha_k}\) ，则 \(n=\sum_{i=1}^k\alpha_i\le 2\cdot 10^5\) 。

根据上面的分析，答案为：

\[[x^{\lfloor\frac n2\rfloor}]\prod_{i=1}^k(1+x+\cdots+x^{\alpha_i}) \]

由于多项式次数为 \(n\) ，我们可以通过分治 NTT 把这个多项式求出来。

常规做法可以类比线段树，每个叶子节点挂一个多项式，求第 \([l,r]\) 个叶子的乘积时只需要把 \([l,m]\) 和 \([m+1,r]\) 卷起来，每层时间复杂度 \(\mathcal O(n\log n)\) ，总共 \(\log n\) 层。

比较优秀的做法是小根堆维护所有需要乘起来的多项式，每次取出两个次数最低的多项式，然后把它们的乘积塞回去。这样时间复杂度仍然是 \(\mathcal O(n\log^2n)\) ，但常数会小一点。

#include<bits/stdc++.h>
#define poly vector<int>
using namespace std;
const int maxn=1<<18,mod=998244353;
int n,x,inv3;
int r[maxn],cnt[3000005];
priority_queue<poly,vector<poly>,greater<poly>> q;
bool operator<(const poly &a,const poly &b)
{
    return a.size()<b.size();
}
int qpow(int a,int k)
{
    int res=1;
    for(;k;k>>=1,a=1ll*a*a%mod) if(k&1) res=1ll*res*a%mod;
    return res;
}
void ntt(poly &a,int n,int op)
{
    for(int i=0;i<n;i++) if(i<r[i]) swap(a[i],a[r[i]]);
    for(int k=2,m=1;k<=n;k<<=1,m<<=1)
    {
        int x=qpow(op==1?3:inv3,(mod-1)/k);
        for(int i=0;i<n;i+=k)
            for(int j=i,w=1;j<i+m;j++)
            {
                int v=1ll*a[j+m]*w%mod;
                a[j+m]=(a[j]-v+mod)%mod,a[j]=(a[j]+v)%mod;
                w=1ll*w*x%mod;
            }
    }
    if(op==-1)
    {
        int inv=qpow(n,mod-2);
        for(int i=0;i<n;i++) a[i]=1ll*a[i]*inv%mod;
    }
}
poly operator*(poly a,poly b)
{
    int n=a.size()-1,m=b.size()-1,len=1;
    while(len<=n+m) len<<=1;
    for(int i=0;i<len;i++) r[i]=(r[i>>1]>>1)|(i&1?len>>1:0);
    a.resize(len),b.resize(len);
    ntt(a,len,1),ntt(b,len,1);
    for(int i=0;i<len;i++) a[i]=1ll*a[i]*b[i]%mod;
    ntt(a,len,-1),a.resize(n+m+1);
    return a;
}
int main()
{
    scanf("%d",&n),inv3=qpow(3,mod-2);
    for(int i=1;i<=n;i++) scanf("%d",&x),cnt[x]++;
    for(int i=1;i<=3000000;i++)
    {
        if(!cnt[i]) continue;
        vector<int> tmp(cnt[i]+1,1);
        q.push(tmp);
    }
    while(q.size()>1)
    {
        poly a=q.top();q.pop();
        poly b=q.top();q.pop();
        q.push(a*b);
    }
    printf("%d\n",q.top()[n/2]);
    return 0;
}

ln + exp

取 \(\ln\) 以后乘法变成了加法，注意到：

\[\ln(1+x+\cdots+x^{\alpha_i})=\ln(1-x^{\alpha_i+1})-\ln(1-x)\\ \ln(1-x^c)=-\sum_{i=1}^\infty\frac{x^{ci}}i\\ \]

证明可以去看例题付公主的背包，我的题解。

于是我们可以以调和级数的复杂度维护取 \(\ln\) 以后的结果，最后 \(\exp\) 回去，时间复杂度 \(\mathcal O(n\log n)\) 。

然而 \(2\log\) 跑得比 \(1\log\) 快。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1<<19,mod=998244353;
int n,x,len,inv3;
int cnt[maxn],tmp[3000005],inum[maxn];
int a[maxn],b[maxn],c[maxn],d[maxn],e[maxn],f[maxn],g[maxn];
int p[maxn],q[maxn],r[maxn];
int qpow(int a,int k)
{
    int res=1;
    for(;k;a=1ll*a*a%mod,k>>=1) if(k&1) res=1ll*res*a%mod;
    return res;
}
void ntt(int *a,int n,int op)
{
    for(int i=0;i<n;i++) if(i<r[i]) swap(a[i],a[r[i]]);
    for(int k=2,m=1;k<=n;k<<=1,m<<=1)
    {
        int x=qpow(op==1?3:inv3,(mod-1)/k);
        for(int i=0;i<n;i+=k)
            for(int j=i,w=1;j<i+m;j++)
            {
                int v=1ll*a[j+m]*w%mod;
                a[j+m]=(a[j]-v+mod)%mod,a[j]=(a[j]+v)%mod;
                w=1ll*w*x%mod;
            }
    }
    if(op==-1)
    {
        int inv=qpow(n,mod-2);
        for(int i=0;i<n;i++) a[i]=1ll*a[i]*inv%mod;
    }
}
void mul(int *a,int *b,int n)
{
    for(int i=0;i<n;i++) p[i]=a[i],q[i]=b[i];
    for(int i=0;i<n;i++) r[i]=(r[i>>1]>>1)|(i&1?n>>1:0);
    ntt(p,n,1),ntt(q,n,1);
    for(int i=0;i<n;i++) a[i]=1ll*p[i]*q[i]%mod;
    ntt(a,n,-1);
}
void inv(int *a,int *b,int n)
{
    for(int i=0;i<n;i++) b[i]=0;
    b[0]=qpow(a[0],mod-2);
    for(int k=2;k<=n;k<<=1)
    {
        for(int i=0;i<2*k;i++) c[i]=i<k?a[i]:0,d[i]=i<k>>1?b[i]:0;
        mul(d,d,k),mul(c,d,k<<1);
        for(int i=0;i<k;i++) b[i]=(2ll*b[i]-c[i]+mod)%mod;
    }
}
void diff(int *a,int *b,int n)
{
    for(int i=1;i<n;i++) b[i-1]=1ll*i*a[i]%mod;
    b[n-1]=0;
}
void integ(int *a,int *b,int n)
{
    for(int i=1;i<n;i++) b[i]=1ll*qpow(i,mod-2)*a[i-1]%mod;
    b[0]=0;
}
void ln(int *a,int *b,int n)
{
    diff(a,e,n),inv(a,f,n),mul(e,f,n<<1),integ(e,b,n);
}
void exp(int *a,int *b,int n)
{
    for(int i=0;i<2*n;i++) b[i]=g[i]=0;
    b[0]=1;
    for(int k=2;k<=n;k<<=1)
    {
        ln(b,g,k);
        for(int i=0;i<k;i++) g[i]=(a[i]-g[i]+mod)%mod;
        g[0]++,mul(b,g,k<<1);
    }
}
int main()
{
    scanf("%d",&n),inv3=qpow(3,mod-2);
    for(int i=1;i<=n;i++) scanf("%d",&x),tmp[x]++;
    for(int i=1;i<=3000000;i++) cnt[tmp[i]+1]++,cnt[1]--;
    for(int i=1;i<=n;i++) inum[i]=qpow(i,mod-2);
    for(int i=1;i<=n;i++)
        if(cnt[i]) for(int j=i;j<=n;j+=i)
            a[j]=(a[j]-1ll*cnt[i]*inum[j/i])%mod;
    for(int i=1;i<=n;i++) a[i]=(a[i]+mod)%mod;
    for(len=1;len<=n;len<<=1) ;
    exp(a,b,len);
    printf("%d\n",b[n>>1]);
    return 0;
}