2-SAT 学习笔记

一、简介

k-SAT (satisfiability) 解决这样一类问题：给定 \(n\) 个布尔变量和 \(m\) 条限制，每条限制形如 \(x_1=0/1\or\cdots\or x_n=0/1\) ，求是否有解并给出构造。

当 \(k\gt 2\) 时，该问题为 NP 完全问题。

二、算法流程

在学习本算法前，请确保你对有向图强连通分量有一定了解。

例1、\(\texttt{P4782 【模板】2-SAT}\)

题目描述

有 \(n\) 个布尔变量 \(x_1,\cdots,x_n\) ， \(m\) 个条件形如 \(x_i=a\or x_j=b\) 。

若存在一组解满足所有条件，给出任意一组构造，否则输出 IMPOSSIBLE 。

数据范围

• \(1\le n,m\le 10^6\) 。
• \(1\le i,j\le n,0\le a,b\le 1\) 。

时间限制 \(\texttt{1s}\) ，空间限制 \(\texttt{512MB}\) 。

分析

先拆点，用 \(i\) 表示 \(x_i=1\) ，用 \(i'\) 表示 \(x_i=0\) 。

• \(a=0,b=0\) ：连边 \(i\to j',j\to i'\) 。
• \(a=0,b=1\) ：连边 \(i\to j,j'\to i'\) 。
• \(a=1,b=0\) ：连边 \(i'\to j',j\to i\) 。
• \(a=1,b=1\) ：连边 \(i'\to j,j'\to i\) 。

以第一种情况为例， \(x_i=0\or x_j=0\) 与下面这两个条件等价：

• 若 \(x_i=1\) ，则 \(x_j=0\) 。
• 若 \(x_j=1\) ，则 \(x_i=0\) 。

其余同理。

---

建模完毕后跑 \(\texttt{tarjan}\) 算法，回忆强联通分量的本质：

\(\forall x,y\in\) 同一强连通分量，存在路径 \(x\to u_1\to\cdots\to u_k\to y\) 和 \(y\to v_1\to\cdots\to v_l\to x\) 。

这两条路径在 2-SAT 中的含义：

• 若 \(x\) 成立，则 \(u_1\) 成立。
• 。。。
• 若 \(u_k\) 成立，则 \(y\) 成立。
• 若 \(y\) 成立，则 \(v_1\) 成立。
• 。。。
• 若 \(v_l\) 成立，则 \(x\) 成立。

换言之， \(x\) 和 \(y\) 互为充要条件。

进一步，有以下结论：

2-SAT 问题有解当且仅当 \(\forall 1\le i\le n\) ， \(i\) 和 \(i'\) 不在同一个强连通分量中。

---

接下来解决输出方案的问题。

拓扑序：给定一张有向无环图，若对于任意一条边 \(u\to v\) ，均有 \(a_u\lt a_v\) ，则称数列 \(a\) 为一个拓扑序。

在 \(\texttt{tarjan}\) 算法中，求出每个点所属强连通分量的编号（博主码风中的 bel 数组）是拓扑序的逆序。

• 若拓扑序 \(a_i\lt a_{i'}\) ，说明若 \(x_i=1\) ，则有可能限制 \(x_i=0\) ；但若 \(x_i=0\) ，一定不会产生限制 \(x_i=1\) 。因此取 \(x_i=0\) 一定符合要求。
• 若拓扑序 \(a_i\gt a_{i'}\) ，说明若 \(x_i=1\) ，则有可能限制 \(x_i=1\) ；但若 \(x_i=1\) ，一定不会产生限制 \(x_i=0\) 。因此取 \(x_i=1\) 一定符合要求。

在代码实现中，\(x_i=1\) 当且仅当 bel[i]<bel[n+i] 。

不建议背结论，一定要理解算法本质，尤其是拓扑序和强连通分量编号一定要绕清楚！

时间复杂度 \(\mathcal O(n+m)\) 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+5;
int m,n,cnt,sum;
int bel[maxn],dfn[maxn],low[maxn];
bool ins[maxn];
stack<int> st;
vector<int> g[maxn];
void addedge(int u,int v)
{
    g[u].push_back(v);
}
void tarjan(int u)
{
    dfn[u]=low[u]=++cnt,st.push(u),ins[u]=true;
    for(auto v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(ins[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        sum++;
        int v;
        do v=st.top(),st.pop(),ins[v]=false,bel[v]=sum;
        while(v!=u);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int a=0,b=0,i=0,j=0;m--;)
    {
        scanf("%d%d%d%d",&i,&a,&j,&b);
        addedge(i+n*a,j+n*!b),addedge(j+n*b,i+n*!a);
    }
    for(int i=1;i<=2*n;i++) if(!dfn[i]) tarjan(i);
    for(int i=1;i<=n;i++) if(bel[i]==bel[n+i]) printf("IMPOSSIBLE\n"),exit(0);
    printf("POSSIBLE\n");
    for(int i=1;i<=n;i++) printf("%d ",bel[i]<bel[n+i]);
    putchar('\n');
    return 0;
}

温馨提示：

• 点数记得开两倍。
• 对于大多数 2-SAT 题目，我们常用 \(2i\) 和 \(2i+1\) 作为一对互补点（而不是加减 \(n\)），这样可以通过 ^1 操作快速找到互补点。

三、对连边的理解

划重点： \(u\to v\) 的边表示若 \(u\) 成立，则 \(v\) 成立。

如果题目表述是 "若 \(u\) ，则 \(v\) " ，千万不要天真地以为只连单向边就够了，因为它还有一个隐藏限制"若 \(v'\) ，则 \(u'\) "。 如果不加后半句话，那么选择 \(v'\) 时没有限制，不符合要求。

在图论建模时，我们要保证连边与题目描述互为充要条件。一般必要性比较显然，但充分性需要我们仔细验证。

对称性

由于一个命题和其逆否命题互为充要条件，所以连边有非常强的对称性，以下是一些常用性质：

• \(i\) 的前驱和 \(i'\) 的后继一一互补。
• 一个强联通分量中所有点的互补点构成另一个强联通分量。

---

还有一些常用的连边小技巧。

强制 \(x_i=0\)

连边 \(i\to i'\) 。

强制 \(x_i=1\)

连边 \(i'\to i\) 。

\(x_i\) 与 \(x_j\) 取值相同

连边 \(i\to j,j\to i,i'\to j',j'\to i'\) 。

这些连边都不会破坏对称性。

四、最小字典序

例2、\(\texttt{HDU1814 Peaceful Commission}\)

题目描述

\(n\) 个政党，第 \(i\) 个政党有两名代表，编号分别为 \(2i-1\) 和 \(2i\) 。

\(m\) 条关系 \((a,b)\) ，表示编号为 \(a\) 和 \(b\) 的代表不喜欢对方。

现在要从每个政党中选择一名代表加入和平委员会，要求委员会中的人不能不喜欢对方。

若不能构建和平委员会，输出 NIE ；否则输出字典序最小的编号序列。

数据范围

本题有多组数据。

• \(1\le n\le 8000,1\le m\le 20000\) 。
• \(1\le a\lt b\le 2n\) 。

时间限制 \(\texttt{5s}\) ，空间限制 \(\texttt{32MB}\) 。

分析

重题 \(\texttt{P5782 [POI2001] 和平委员会}\) ，但是没有要求最小字典序。

连边非常简单， \(a\to b',b\to a'\) 。

逐一遍历每个政党，如果 \(i\) 和 \(i'\) 都没被标记过，钦定先取 \(i\) 。

根据图中的边爆搜出一定被选的点，一边搜一边打标记，如果已经标记过就不用再搜了，如果互补点被标记过就说明矛盾。

如果搜索成功就保留标记，这是钦定取 \(i\) 带来的限制；如果搜索失败就回退标记再尝试取 \(i'\) ，依然失败则说明无解。

对上述算法正确性的感性理解

我们担心的就是这样一个问题：现在取 $i$ 合法，却导致以后 $j$ 和 $j'$ 都要取，但是取 $i'$ 可以避开。

事实上，这种情况不可能出现。在缩点后的图中考虑，我们会搜索到所有 $i$ 的后继节点。

因此 $j$ 和 $j'$ 都有比 $i$ 更小的拓扑序，若从 $j$ 出发能搜到 $j'$ ，只能是 $j$ 和 $j'$ 在同一个强连通分量中，而不可能中途经过 $i$ 。

时间复杂度 \(\mathcal O(nm)\) ，但是很难跑满。

#include<bits/stdc++.h>
using namespace std;
const int maxn=16005;
int m,n,top;
int st[maxn];
bitset<maxn> vis;
vector<int> g[maxn];
void addedge(int u,int v)
{
    g[u].push_back(v);
}
bool dfs(int u)
{
    if(vis[u]) return true;
    if(vis[u^1]) return false;
    vis[u]=true,st[++top]=u;
    for(auto v:g[u]) if(!dfs(v)) return false;
    return true;
}
void work()
{
    for(int i=0;i<2*n;i++) g[i].clear();
    vis.reset();
    for(int a=0,b=0;m--;)
    {
        scanf("%d%d",&a,&b),a--,b--;
        addedge(a,b^1),addedge(b,a^1);
    }
    for(int i=0;i<2*n;i+=2)
        if(!vis[i]&&!vis[i^1])
        {
            top=0;
            if(dfs(i)) continue;
            while(top) vis[st[top--]]=0;
            if(!dfs(i^1)) return printf("NIE\n"),void();
        }
    for(int i=0;i<2*n;i++) if(vis[i]) printf("%d\n",i+1);
}
int main()
{
    while(~scanf("%d%d",&n,&m)) work();
    return 0;
}

例3、\(\texttt{CF568C New Language}\)

题目描述

对于长为 \(l\) 的字符集，给定每个字符属于 \(\texttt{V}\) 集合还是 \(\texttt{C}\) 集合。

给定长为 \(n\) 的字符串 \(s\) ，你需要构造一个长为 \(n\) 且字典序不小于 \(s\) 的字符串 \(t\) ，满足如下 \(m\) 个限制：

• 若 \(t_{p_1}\in c_1\) ，则 \(t_{p_2}\in c_2\) 。

数据范围

• \(1\le l\le 26,1\le n\le 200,0\le m\le 4n(n-1)\) 。
• \(1\le p_1,p_2\le n\) ， \(c_1,c_2\in\{\texttt{T},\texttt{C}\}\) 。

时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{256MB}\) 。

分析

看到 "若…则…" 型限制千万不要只连单向边，其逆否命题也要连边。

字典序限制按位贪心即可，枚举第一次在哪脱落限制，细节较多。

然后和上题一样跑 \(\texttt{dfs}\) ，时间复杂度 \(\mathcal O(n^2m)\) 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=405;
int l,m,n,top;
char c,d,s[maxn],t[maxn];
int st[maxn];
bitset<maxn> b,vis;
vector<int> g[maxn];
void addedge(int u,int v)
{
    g[u].push_back(v);
}
bool dfs(int u)
{
    if(vis[u]) return true;
    if(vis[u^1]) return false;
    vis[u]=true,st[++top]=u;
    for(auto v:g[u]) if(!dfs(v)) return false;
    return true;
}
void check(int o)
{
    if(s[o]=='a'+l-1) return ;
    top=0,vis.reset();
    for(int i=0;i<o;i++) if(!dfs(2*i+b[s[i]])) return ;
    for(int i=0;i<o;i++) t[i]=s[i];
    for(int i=o;i<n;i++)
    {
        t[i]=i==o?s[i]+1:'a',top=0;
        if(dfs(2*i+b[t[i]])) continue;
        while(top) vis[st[top--]]=0;
        int flg=b[t[i]];
        while(t[i]<='a'+l-1)
        {
            if(b[t[i]]==flg) t[i]++;
            else if(dfs(2*i+b[t[i]])) break;
            else t[i]='a'+l;
        }
        if(t[i]=='a'+l) return ;
    }
    printf("%s\n",t),exit(0);
}
int main()
{
    scanf("%s%d%d",s,&n,&m),l=strlen(s);
    for(int i=0;i<l;i++) b['a'+i]=s[i]=='C';
    for(int x=0,y=0;m--;)
    {
        scanf("%d %c %d %c",&x,&c,&y,&d);
        int u=2*x-2+(c=='C'),v=2*y-2+(d=='C');
        addedge(u,v),addedge(v^1,u^1);
    }
    scanf("%s",s);
    for(int o=n;o>=0;o--) check(o);
    printf("-1\n");
    return 0;
}

五、相关例题

例4、\(\texttt{P3513 [POI2011] KON-Conspiracy}\)

题目描述

\(n\) 个人，给定每两人是否为熟人关系。

现在将这些人划分成后勤和同谋两部分，要求：

• 后勤中任意两人都必须是熟人。
• 同谋中任意两人都不是熟人。
• 每一部分至少有一个人。

求方案数。

数据范围

• \(2\le n\le 5000\) 。

时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{250MB}\) 。

分析

一般的 2-SAT 问题不能计数，本题利用了某些特殊性质。

忽略第三个条件，先用 2-SAT 跑出任意一组解，如果跑不出来则输出 \(0\) 。

容易证明所有解都可以在已经得到的解的基础上通过以下两种操作之一得到：

• 将某个人移到另一组。
• 从两组中分别选一个人，然后对调。

想一想，为什么？

不可能将同一组中的两个人同时拿到另一组去。比如说两个人都在后勤，那么他们一定是熟人，从而不可能同时出现在同谋中。

记 \(cnt_i\) 表示若将 \(i\) 移到另一组会与多少人发生冲突， \(id_i\) 为发生冲突的人的编号（如果有多个则任选一个）。

若 \(cnt_i\ge 2\) ，显然第 \(i\) 个人不可能进行任何操作。

第一种情况显然方案数为 \(\sum_{i=1}^n[cnt_i=0]\) 。

对于第二种情况，假设我们要调换 \(u,v\) ：

• \(cnt_u=1,cnt_v=1\) ：理论上要求 \(u,v\) 互为冲突，但这种情况不可能发生，因为 \(u,v\) 之间不可能既有边又没边。
• \(cnt_u=1,cnt_v=0\) ：要求 \(id_u=v\) 。
• \(cnt_u=0,cnt_v=0\) ：这种情况的总方案数为 \(\sum\limits_{u\in 后勤}[cnt_u=0]\times\sum\limits_{v\in 同谋}[cnt_v=0]\) 。

第三个条件总共就两种情况，特判一下就好了。

从上述分析中可以看出答案 \(\le\mathcal O(n^2)\) ，实际上答案是 \(\mathcal O(n)\) 级别，证明不会所以略去。

时间复杂度 \(\mathcal O(n^2)\) 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=10005;
int m,n,idx,sum;
int bel[maxn],dfn[maxn],low[maxn];
int id[maxn],cnt[maxn],tmp[2];
bool ins[maxn];
bitset<5005> a,b[5005];
stack<int> st;
vector<int> g[maxn];
void addedge(int u,int v)
{
    g[u].push_back(v);
}
void tarjan(int u)
{
    dfn[u]=low[u]=++idx,st.push(u),ins[u]=true;
    for(auto v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(ins[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        int v;
        sum++;
        do v=st.top(),st.pop(),ins[v]=false,bel[v]=sum;
        while(v!=u);
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1,k=0,x=0;i<=n;i++)
    {
        scanf("%d",&k),m+=k;
        while(k--) scanf("%d",&x),b[i][x]=1;
    }
    if(!m||m==n*(n-1)) printf("%d\n",n),exit(0);
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
            if(!b[i][j]) addedge(2*i-1,2*j),addedge(2*j-1,2*i);
            else addedge(2*i,2*j-1),addedge(2*j,2*i-1);
    for(int i=1;i<=2*n;i++) if(!dfn[i]) tarjan(i);
    for(int i=1;i<=n;i++) if(bel[2*i-1]==bel[2*i]) printf("0\n"),exit(0);
    for(int i=1;i<=n;i++) a[i]=bel[2*i-1]<bel[2*i];
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
            if(a[j]!=a[i]&&a[j]!=b[i][j])
                    cnt[i]++,id[i]=j;
        if(!cnt[i]) tmp[a[i]]++;
    }
    int res=(tmp[0]+1)*(tmp[1]+1);
    for(int i=1;i<=n;i++) res+=cnt[i]==1&&!cnt[id[i]];
    printf("%d\n",res);
    return 0;
}

例5、\(\texttt{P3825 [NOI2017] 游戏}\)

题目描述

\(3\) 辆赛车，用 \(A,B,C\) 表示。

\(4\) 种地图，用 \(x,a,b,c\) 表示。

其中 \(A\) 赛车不能用于 \(a\) 地图， \(B\) 赛车不能用于 \(b\) 地图， \(C\) 赛车不能用于 \(c\) 地图。 \(x\) 地图适合所有赛车，但数量不超过 \(d\) 。

\(n\) 场游戏，给定每场游戏使用的地图。

\(m\) 条规则，若第 \(i\) 场使用型号为 \(h_i\) 的赛车，则第 \(j\) 场必须使用型号为 \(h_j\) 的赛车。

判断是否存在一种方案满足所有规则。若能，输出每场游戏使用的赛车型号，否则输出 -1 。

数据范围

• \(0\le n\le 5\cdot 10^4,1\le m\le 10^5,0\le d\le 8\) 。
• \(1\le i,j\le n,h_i,h_j\in\{A,B,C\}\) 。

时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{512MB}\) 。

分析

先考虑 \(d=0\) 的情况，此时不存在 \(x\) 地图。

• 对 \(a\) 地图，令 \(i\) 表示使用 \(B\) 赛车， \(i'\) 表示使用 \(C\) 赛车。
• 对 \(b\) 地图，令 \(i\) 表示使用 \(C\) 赛车， \(i'\) 表示使用 \(A\) 赛车。
• 对 \(c\) 地图，令 \(i\) 表示使用 \(A\) 赛车， \(i'\) 表示使用 \(B\) 赛车。

按题目限制连边，接下来是一个裸的 2-SAT 问题。

当 \(d\neq 0\) 时，暴力枚举把每张 \(x\) 地图当成 \(a\) 地图还是 \(b\) 地图，由于 \(a\) 地图适合 \(B,C\) 赛车， \(b\) 地图适合 \(C,A\) 赛车，所以可以覆盖所有情况。

时间复杂度 \(\mathcal O\big(2^d(n+m)\big)\) 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int d,m,n,cnt,sum;
int pos[8];
char s[maxn];
int bel[maxn],dfn[maxn],low[maxn];
bool ins[maxn];
stack<int> st;
vector<int> g[maxn];
struct node
{
    int x,y;
    char c,d;
    void read()
    {
        scanf("%d %c %d %c",&x,&c,&y,&d);
        x--,y--,c+=32,d+=32;
    }
}e[maxn];
void addedge(int u,int v)
{
    g[u].push_back(v);
}
int get_id(int x,char c)
{
    if(s[x]==c) return -1;
    return 2*x+((s[x]-c+3)%3==1);
}
void tarjan(int u)
{
    dfn[u]=low[u]=++cnt,st.push(u),ins[u]=true;
    for(auto v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(ins[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        int v;
        sum++;
        do v=st.top(),st.pop(),ins[v]=false,bel[v]=sum;
        while(v!=u);
    }
}
int main()
{
    scanf("%d%d%s%d",&n,&d,s,&m);
    for(int i=1;i<=m;i++) e[i].read();
    for(int i=0,j=0;i<n;i++) if(s[i]=='x') pos[j++]=i;
    for(int u=0;u<1<<d;u++)
    {
        cnt=sum=0;
        for(int i=0;i<2*n;i++) g[i].clear(),dfn[i]=low[i]=0;
        for(int i=0;i<d;i++) s[pos[i]]='a'+(u>>i&1);
        for(int i=1;i<=m;i++)
        {
            int u=get_id(e[i].x,e[i].c),v=get_id(e[i].y,e[i].d);
            if(u!=-1&&v!=-1) addedge(u,v),addedge(v^1,u^1);
            else if(u!=-1) addedge(u,u^1);
        }
        for(int i=0;i<2*n;i++) if(!dfn[i]) tarjan(i);
        int flg=1;
        for(int i=0;i<2*n;i+=2) flg&=bel[i]!=bel[i^1];
        if(!flg) continue;
        for(int i=0;i<n;i++) putchar('A'+(s[i]-'a'+(bel[2*i]<bel[2*i+1]?1:2))%3);
        putchar('\n'),exit(0);
    }
    printf("-1\n");
    return 0;
}

例6、\(\texttt{P6378 [PA2010] Riddle}\)

题目描述

\(n\) 个点 \(m\) 条边的无向图被分成 \(k\) 个部分，每个部分包含一些点。

请选择一些关键点，使得每个部分恰有一个关键点，且每条边至少有一个端点是关键点。

数据范围

• \(1\le k\le n\le 10^6,0\le m\le 10^6\) 。

时间限制 \(\texttt{3s}\) ，空间限制 \(\texttt{512MB}\) 。

分析

每条边 \((u,v)\) 的限制等价于 \(u'\to v,v'\to u\) 。

对于每个部分中的点 \(u_1,\cdots,u_l\) ，我们需要连边 \(u_i\to u'_j\) （ \(i\neq j\) ）。

使用前缀优化建图的思想，按照下图的方法，建立一排虚点，可以实现连向后缀所有点。

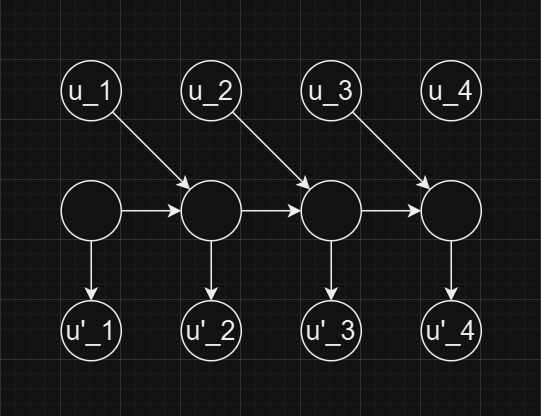
前缀同理，再来一遍即可。

时间复杂度 \(\mathcal O(n+m)\) 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=4e6+5;
int k,m,n,cnt,idx,sum;
int a[maxn],pre[maxn],suf[maxn];
int bel[maxn],dfn[maxn],low[maxn];
bool ins[maxn];
stack<int> st;
vector<int> g[maxn];
void addedge(int u,int v)
{
    if(u&&v) g[u].push_back(v);
}
void tarjan(int u)
{
    dfn[u]=low[u]=++idx,st.push(u),ins[u]=true;
    for(auto v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(ins[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        int v;
        sum++;
        do v=st.top(),st.pop(),ins[v]=false,bel[v]=sum;
        while(v!=u);
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&k),cnt=2*n;
    for(int u=0,v=0;m--;)
    {
        scanf("%d%d",&u,&v);
        addedge(2*u,2*v-1),addedge(2*v,2*u-1);
    }
    for(int l=0;k--;)
    {
        scanf("%d",&l),suf[l+1]=0;
        for(int i=1;i<=l;i++)
        {
            scanf("%d",&a[i]);
            addedge(pre[i]=++cnt,2*a[i]),addedge(suf[i]=++cnt,2*a[i]);
        }
        for(int i=1;i<l;i++) addedge(pre[i+1],pre[i]),addedge(suf[i],suf[i+1]);
        for(int i=1;i<=l;i++) addedge(2*a[i]-1,pre[i-1]),addedge(2*a[i]-1,suf[i+1]);
    }
    for(int i=1;i<=cnt;i++) if(!dfn[i]) tarjan(i);
    for(int i=1;i<=n;i++) if(bel[2*i-1]==bel[2*i]) printf("NIE\n"),exit(0);
    printf("TAK\n");
    return 0;
}

例7、\(\texttt{CF1215F Radio Stations}\)

题目描述

有 \(p\) 个电站，每个电站有开启和关闭两种状态。

有 \(n\) 条限制，要求 \(x\) 电站和 \(y\) 电站至少一个处于开启状态。

有 \(m\) 条限制，要求 \(x\) 电站和 \(y\) 电站至多一个处于开启状态。

你可以在 \([1,M]\) 中选择主频 \(f\)。第 \(i\) 个电站有参数 \(l_i,r_i\) ，若 \(f\in [l_i,r_i]\) ，你可以自行决定第 \(i\) 个电站是否开启，否则必须关闭。

判断是否存在一种方案满足上述所有限制，若存在，输出主频 \(f\) 和所有开启的电站编号，否则输出 -1 。

数据范围

• \(2\le m,n,p,M\le 4\cdot 10^5\) 。
• \(1\le x\le y\le p,1\le l_i\le r_i\le M\) 。

时间限制 \(\texttt{7s}\) ，空间限制 \(\texttt{256MB}\) 。

分析

前两类限制如何连边已经被讲烂了，这里直接略去。

额外开 \(2(M+1)\) 个点，对 \(\forall 0\le i\le M\) ，用 \(2p+i,2p+i'\) 表示 \(f\le i\) 是否成立。

先看我们的限制表述：

• 若 \(f\in [l_i,r_i]\) ，则 \(i\) 。

将它翻译成 "若 … 则 …" 的形式：

• 若 \(f\le l_i-1\) ，则 \(i'\) 。
• 若 \(f\not\le r_i\) ，则 \(i'\) 。
• 若 \(i\) ，则 \(f\not\le l_i-1\) 。
• 若 \(i\) ，则 \(f\le r_i\) 。

可以验证两者互为充要条件。

这里依然用到了前缀优化建图的思想，如果新点表示的是 \([f=i]\) 是否成立，则我们需要实现点向区间连边，无论是使用线段树还是猫树，时空复杂度都会带上一只 \(\log\) 。

验证充要这一步非常重要！虽然代码里体现不出来，但是它直接决定了如何建图。

还有最后一个细节，\(f\le 0\) 一定不成立，连边 \(2p+0\to 2p+0'\) 即可。

时间复杂度 \(\mathcal O(n+m+p+M)\) 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1.6e6+5;
int a,b,f,m,n,p,cnt,sum;
int bel[maxn],dfn[maxn],low[maxn];
bool ins[maxn];
stack<int> st;
vector<int> g[maxn],vec;
void addedge(int u,int v)
{
    g[u].push_back(v);
}
void tarjan(int u)
{
    dfn[u]=low[u]=++cnt,st.push(u),ins[u]=true;
    for(auto v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(ins[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        sum++;
        int v;
        do v=st.top(),st.pop(),bel[v]=sum,ins[v]=false;
        while(v!=u);
    }
}
int main()
{
    scanf("%d%d%d%d",&a,&p,&m,&b);
    for(int i=1,x=0,y=0;i<=a;i++)
    {
        scanf("%d%d",&x,&y);
        addedge(2*x,2*y-1),addedge(2*y,2*x-1);
    }
    for(int i=1,l=0,r=0;i<=p;i++)
    {
        scanf("%d%d",&l,&r);
        addedge(2*i-1,2*p+2*l),addedge(2*i-1,2*p+2*r+1);
        addedge(2*p+2*l-1,2*i),addedge(2*p+2*r+2,2*i);
    }
    for(int i=1,x=0,y=0;i<=b;i++)
    {
        scanf("%d%d",&x,&y);
        addedge(2*x-1,2*y),addedge(2*y-1,2*x);
    }
    addedge(2*p+1,2*p+2);
    for(int i=1;i<=m;i++)
    {
        addedge(2*p+2*i-1,2*p+2*i+1);
        addedge(2*p+2*i+2,2*p+2*i);
    }
    n=p+m+1;
    for(int i=1;i<=2*n;i++) if(!dfn[i]) tarjan(i);
    for(int i=1;i<=n;i++) if(bel[2*i-1]==bel[2*i]) printf("-1\n"),exit(0);
    for(int i=1;i<=p;i++) if(bel[2*i-1]<bel[2*i]) vec.push_back(i);
    for(int i=1;i<=m;i++)
        if(bel[2*p+2*i-1]>bel[2*p+2*i]&&bel[2*p+2*i+1]<bel[2*p+2*i+2])
            f=i;
    printf("%d %d\n",vec.size(),f);
    for(auto i:vec) printf("%d ",i);
    putchar('\n');
    return 0;
}