UNR #8 题解
uoj887 最酷的排列
题目描述
\(T\) 组数据，给定长为 \(n\) 的序列 \(a\) 和下标集合 \(S\) ，你可以对序列进行任意次操作，每次选择一个区间并将其中元素升序排序。
求 \(\sum\limits_{i\in S}a_i\) 的最小可能值。
数据范围
- \(1\le n,\sum n\le 2\cdot 10^5,1\le a_i\le 10^9\)。
时间限制 \(\texttt{1s}\) ，空间限制 \(\texttt{1024MB}\)。
分析
注意到对一个区间排序等价于进行若干次冒泡，因此只需选择长为 \(2\) 的区间。
根据 \(\texttt{Subtask3}\) 的提示，从后往前扫描，最终某个位置的数不可能比已经扫描过的位置更小，即 \(a'_i\ge \min\limits_{i\le j\le n}a_j\)。
小根堆维护已经扫描且尚未使用过的数，每次碰到集合 \(S\) 中的下标，弹出其中的最小值，这是答案的下界。
再来证明上述方法得到的答案可以取到，对于 \(S\) 中的两个相邻下标 \(i,j\) ，如果在 \(i\) 处弹出的数（记为 \(b_i\)）比 \(j\) 处（记为 \(b_j\)）大，每次交换两个数可以让 \(a'_i=b_j,a'_j=b_i\) ，即完成 \(S\) 内部的冒泡。
时间复杂度 \(\mathcal O(\sum n\log n)\)。
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int n,t;
long long res;
int a[maxn];
char s[maxn];
int main()
{
for(scanf("%d",&t);t--;)
{
scanf("%d",&n),res=0;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
scanf("%s",s+1);
priority_queue<int,vector<int>,greater<int>> q;
for(int i=n;i>=1;i--)
{
q.push(a[i]);
if(s[i]=='1') res+=q.top(),q.pop();
}
printf("%lld\n",res);
}
return 0;
}
uoj888 里外一致
题目描述
给定长为 \(n\) 的序列 \(a\) ， \(q\) 次询问，每次给定 \(l,r\) ，求有多少 \(U=\{l,\cdots,r\}\) 的子集 \(S\) 满足 \(|\{a_i|i\in S\}|=|\{a_i|i\in U/S\}|\) ，对 \(2^{64}\) 取模。
数据范围
- \(1\le n\le 3\cdot 10^5,1\le q\le 10^5,1\le a_i\le n\)。
时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{1024MB}\) 。
分析
先考虑 \(q=1\) 怎么做，假设不同数字在序列 \(a\) 中的出现次数分别为 \(cnt_1,\cdots,cnt_m\)。
\(f_{i,j}\) 表示考虑前 \(i\) 个 \(cnt\) ，\(|\{a_i|i\in S\}|-|\{a_i|i\in U/S\}|=j\) 的方案数。
容易写出转移方程：
用生成函数的视角理解，答案为：
本题非常 \(\texttt{tricky}\) 的一点是，由于答案对 \(2^{64}\) 取模，所以如果与\(2^{cnt_i}\)有关的项取太多对答案没有任何影响。
将 \(x-2+\frac 1x\) 和 \(2^{cnt_i}\) 拆开来看，注意到：
\(g_{i,j}\) 表示考虑前 \(i\) 个 \(cnt\) ，有 \(j\) 项没选 \(2^{cnt_i}\) 的系数之和，那么答案为 \(\sum g_{m,j}V_{m-j}\) 。
转移方程 \(g_{i,j}=g_{i-1,j}+2^{cnt_i}\cdot g_{i-1,j-1}\) ，注意到第二维上限为 \(63\) ，否则对答案没有贡献。
预处理 \(V_k\) 即可获得一个 \(\mathcal O(64nq)\) 的做法，link。具体的，预处理阶乘中 \(2\) 的幂次，奇数部分的逆元可以用欧拉定理求出。
注意到 \(g\) 的转移本质上是背包，而背包问题可以支持撤回，用莫队维护 \(cnt\) 和 \(g\) 数组，可以做到 \(\mathcal O(64n\sqrt q)\)。
由于 \(q\) 很小，并且 \(cnt\ge 64\) 时没有贡献，我们希望将所有相同的 \(cnt\) 放在一起转移，这样可以把 \(64\) 的常数从 \(n\sqrt q\) 上拿下来。
记 \(cnt_i=x\) 出现了 \(c_x\) 次，将 \(g\) 的定义修改为考虑所有 \(cnt\le i\) 的情况，转移方程为 \(g_{i,k}\gets\binom{c_x}{k-j}\cdot 2^{i\cdot (k-j)}\cdot g_{i-1,j}\) 。
时间复杂度 \(\mathcal O(n\sqrt q+12243\cdot q)\) ，惊险通过。
这里 \(12243\) 是实测三层循环卡满的转移次数，
如果被叉了可以叫我。注意非常重要的一点，下面代码中第 \(62\) 行 \(x\) 一定要倒序枚举，这样可以大幅减少转移次数。
#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int B=1000,maxn=6e5+5;
int l,n,q,r;
int a[maxn],c[65],pw[maxn],bel[maxn],cnt[maxn];
ull fac[maxn],inv[maxn];
ull g[64],v[maxn],res[maxn];
struct node
{
int l,r,id;
bool operator<(const node &a)
{
return bel[l]!=bel[a.l]?l<a.l:r<a.r;
}
}f[maxn];
ull qpow(ull a,ull k)
{
ull res=1;
for(;k;a=a*a,k>>=1) if(k&1) res=res*a;
return res;
}
ull get_c(int n,int m)
{
int x=pw[n]-pw[m]-pw[n-m];
return x<64?(fac[n]*inv[m]*inv[n-m])<<x:0;
}
void init(int n)
{
fac[0]=1;
for(int i=1,j=0;i<=n;i++)
{
for(j=i,pw[i]=pw[i-1];!(j&1);j>>=1,pw[i]++) ;
fac[i]=fac[i-1]*j;
}
inv[n]=qpow(fac[n],(1ll<<63)-1);
for(int i=n,j=0;i>=1;i--)
{
for(j=i;!(j&1);j>>=1) ;
inv[i-1]=inv[i]*j;
}
for(int i=0;i<=(n>>1);i++) v[i]=(i&1?-1:1)*get_c(i<<1,i);
}
void add(int x,int v)
{
c[min(cnt[x],64)]--,cnt[x]+=v,c[min(cnt[x],64)]++;
}
int main()
{
scanf("%d%d",&n,&q),init(n<<1);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),bel[i]=(i-1)/B+1;
for(int i=1;i<=q;i++) scanf("%d%d",&f[i].l,&f[i].r),f[i].id=i;
sort(f+1,f+q+1);
for(int i=1,l=1,r=0;i<=q;i++)
{
while(l>f[i].l) add(a[--l],1);
while(r<f[i].r) add(a[++r],1);
while(l<f[i].l) add(a[l++],-1);
while(r>f[i].r) add(a[r--],-1);
int m=c[64];
for(int j=0;j<64;j++) g[j]=!j;
for(int x=63;x>=1;x--)
{
m+=c[x];
for(int j=63;j>=0;j--)
if(g[j]) for(int k=min({c[x],63-j,63/x});k>=1;k--)
g[j+k]+=(get_c(c[x],k)*g[j])<<(k*x);
}
for(int j=0;j<=min(m,63);j++) res[f[i].id]+=g[j]*v[m-j];
}
for(int i=1;i<=q;i++) printf("%llu\n",res[i]);
return 0;
}
uoj889 二维抄袭检测
题目描述
给定长为 \(L\) 的字符串 \(s\) 和 \(n\times m\) 的字符矩阵 \(t\) 。
定义可行路径为从字符矩阵中某个点开始，每次向右或向下走一步，不走出边界的路径。
\(q\) 次询问，给定 \(x_i,y_i,p_i\) ，求最大的 \(k\) 满足，存在一条从 \((x_i,y_i)\) 出发、长为 \(k\) 的可行路径，使其对应的字符串为\(s_{p_i}\cdots s_{p_i+k-1}\) 。
数据范围
- \(1\le L\le 10^6\) 。
- \(1\le n\le 10,1\le m\le 5\cdot 10^4\) 。
- \(1\le q\le 10^6\) 。
- \(1\le x_i\le n,1\le y_i\le m,1\le p_i\le L\) 。
时间限制 \(\texttt{4s}\) ，空间限制 \(\texttt{1024MB}\) 。
分析
\(n\le 4\) 时有贪心做法，与正解无关所以此处略去。
为方便后续优化，将矩阵中第 \(i\) 行的字符向右平移 \(i-1\) 个单位，从而每次需要向右或向右下走一步。
\(f_{i,j}\) 表示能否匹配到第 \(i\) 列第 \(j\) 行，可以转移到 \(f_{i+1,j}\) 和 \(f_{i+1,j+1}\) （条件略去）。
注意到第一维每次加一，并且第二维长度 \(\le 10\) ，考虑矩阵乘法优化。
01矩阵的(|,&)乘法的转移形式如下：for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) c[i][j]|=a[i][k]&b[k][j];如果用
bitset进行压位，转移形式变成：for(int i=1;i<=n;i++) for(int k=1;k<=n;k++) if(a[i][k]) c[i]|=b[k];当 \(n\) 比较大的时候，可以给时间复杂度除掉一个 \(w\) 。
由于本题 \(n\le w\) ，所以单次矩阵乘法的时间复杂度为 \(O(n^2)\) 。特别地，向量乘矩阵的时间复杂度为 \(\mathcal O(n)\) 。
然而，第 \(k\) 个转移矩阵由第 \(y_i+k\) 列的字符和 \(s_{p_i+k}\) 共同决定。换言之，不同询问的转移矩阵是不同的。
我们找到当前可以匹配的最小行数（即最小的 \(j\) 满足 \(f_{i,j}=1\)），求出它在这一行能够匹配的最长距离，再做一次暴力转移，此后 \(j\) 至少加一。
由于 \(j\le n\) ，所以上述操作最多重复 \(n\) 次。匹配过程中的转移矩阵仅由匹配的这段字符决定，我们只需要快速求出一行中某段区间的矩阵连乘积。
对每行分别建猫树，询问时用向量乘矩阵，预处理复杂度 \(\mathcal O(n\cdot m\log m\cdot n^2)\) ，询问复杂度 \(\mathcal O(qn\cdot n)\) 。
对满二叉树建猫树，深度相同节点 \(x\) 和 \(y\) 的 \(\texttt{lca}\) 是
x>>(lg[x^y]+1)，其深度为lg[x]-lg[x^y]-1（默认根节点深度为 \(0\)）。对于任意区间 \([i,i]\) （\(0\le i\lt 2^n\)），它对应节点 \(i+2^n\) ，深度最深且相同。
对于区间 \([l,r]\) ，它的根节点为 \([l,l]\) 和 \([r,r]\) 的 \(\texttt{lca}\) 。
从而我们可以 \(\mathcal O(1)\) 找到根节点，即切割 \([l,r]\) 的节点。
求最长匹配距离最简单的方法是哈希加二分，但是容易被叉。将字符串 \(s\) 和字符矩阵 \(t\) 拼在一起建后缀数组，于是转化为经典问题求两个后缀的\(\texttt{lcp}\) 。
时间复杂度 \(\mathcal O((L+nm)\log (L+nm)+n^3m\log m+n^2q)\) 。
下面代码给重点部分加了注释，想看无注释版本的代码可以点这里。
#include<bits/stdc++.h>
using namespace std;
const int maxl=1.5e6+5;
int l,m,n,q,dep;
char s[maxl],t[10][1<<16];
int lg[maxl];
namespace sa
{///后缀数组求lcp
int n;
int c[maxl],x[maxl],y[2*maxl];
int h[maxl],rk[maxl],sa[maxl];
int f[21][maxl];
void get_sa()
{
int m=122;
for(int i=1;i<=n;i++) c[x[i]=s[i]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i>=1;i--) sa[c[x[i]]--]=i;
for(int k=1;k<=n;k<<=1)
{
int num=0;
for(int i=n-k+1;i<=n;i++) y[++num]=i;
for(int i=1;i<=n;i++) if(sa[i]>k) y[++num]=sa[i]-k;
for(int i=1;i<=m;i++) c[i]=0;
for(int i=1;i<=n;i++) c[x[i]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i>=1;i--) sa[c[x[y[i]]]--]=y[i];
for(int i=1;i<=n;i++) y[i]=x[i],x[i]=0;
num=x[sa[1]]=1;
for(int i=2;i<=n;i++)
x[sa[i]]=y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]?num:++num;
if(num==n) break;
m=num;
}
}
void get_height()
{
for(int i=1;i<=n;i++) rk[sa[i]]=i;
for(int i=1,k=0;i<=n;i++)
{
if(k) k--;
int j=sa[rk[i]-1];
while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k]) k++;
h[rk[i]]=k;
}
}
void init(int _n)
{
n=_n,get_sa(),get_height();
for(int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<=n;i++) f[0][i]=h[i];
for(int j=1;j<=lg[n];j++)
for(int i=1;i+(1<<j)-1<=n;i++)
f[j][i]=min(f[j-1][i],f[j-1][i+(1<<(j-1))]);
}
int lcp(int i,int j)
{
if(rk[i]>rk[j]) swap(i,j);
int l=rk[i]+1,r=rk[j],k=lg[r-l+1];
return min(f[k][l],f[k][r-(1<<k)+1]);
}
}
struct vec
{
short v;
vec (short _v=0)
{
v=_v;
}
bool get(int x)
{
return v>>x&1;
}
};
struct mat
{
short v[10];
mat ()
{
for(int i=0;i<n;i++) v[i]=0;
}
bool get(int x,int y)
{
return v[x]>>y&1;
}
void set(int x,int y)
{
if(x!=-1) v[x]|=1<<y;
}
}o;
vec operator*(vec &a,mat &b)
{
vec c;
for(int i=0;i<n;i++) if(a.get(i)) c.v|=b.v[i];
return c;
};
mat operator*(mat &a,mat &b)
{
mat c;
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a.get(i,k)) c.v[i]|=b.v[k];
return c;
}
struct meow
{
mat a[17][1<<17];
void build(int p,int l,int r,int d,int id)
{///(p,l,r)定义同线段树,深度为d,对应字符矩阵中第id行
if(l==r)
{
for(int i=id;i<n;i++) if(t[i][l]==t[id][l]) a[d][l].set(i-1,i),a[d][l].set(i,i);
return ;
}
int mid=(l+r)>>1;
build(p<<1,l,mid,d+1,id),build(p<<1|1,mid+1,r,d+1,id);
mat cur=o;///单位矩阵
for(int i=mid;i>=l;i--) cur=a[dep][i]*cur,a[d][i]=cur;
cur=o;
for(int i=mid+1;i<=r;i++) cur=cur*a[dep][i],a[d][i]=cur;
}
void query(int l,int r,vec &res)
{
if(l==r) res=res*a[dep][l];
else
{
int d=dep-lg[l^r]-1;
///令x=l+(1<<dep),y=l+(1<<dep)
///则d=lg[x]-lg[x^y]-1,注意别忘了减一
res=res*a[d][l],res=res*a[d][r];///向量乘矩阵
}
}
}T[10];
int main()
{
scanf("%d%d%d%d%s",&l,&n,&m,&q,s+1);
for(int i=0;i<n;i++) scanf("%s",t[i]+i);
for(int i=0,k=l;i<n;i++) for(int j=0;j<m;j++) s[++k]=t[i][i+j];
sa::init(l+n*m),dep=lg[m+n-2]+1;
for(int i=0;i<n;i++) o.set(i,i);
for(int i=0;i<n;i++) T[i].build(1,0,(1<<dep)-1,0,i);
s[l+1]=' ';///防止暴力转移时匹配越界
for(int p=0,x=0,y=0;q--;)
{
scanf("%d%d%d",&x,&y,&p),y+=(x--)-2;
if(t[x][y]!=s[p])
{
printf("0\n");
continue;
}
vec res=1<<x;
for(int i=y,j=x;;)
{///f_{i,j}=1满足j最小,res为转移完第i列后的矩阵
///细节拉满,意思就是不能超出s和t的边界
int len=min({sa::lcp(p+i-y,l+j*m+i-j+1),m+j-i,l-p+y-i+1});
assert(len);
if(len>=2) T[j].query(i+1,i+len-1,res);
i+=len;
///暴力转移
vec tmp;
for(int k=j;k<n;k++)
{
if(!res.get(k)) continue;
if(t[k][i]==s[i-y+p]) tmp.v|=1<<k;
if(k+1<n&&t[k+1][i]==s[i-y+p]) tmp.v|=1<<(k+1);
}
res=tmp;
while(j<n&&!res.get(j)) j++;
if(j==n)
{
printf("%d\n",i-y);
break;
}
}
}
return 0;
}
uoj890 兵棋
题目描述
对于长为 \(n\) 的 \(01\) 串 \(s\) ，定义一次操作为，删除所有满足 \(i\ge 2,s_i\neq s_{i-1}\) 的位置，并将剩余位置拼接起来。
给定长为 \(n\) 的由 \(0,1,?\) 组成的字符串 \(s\)，对于所有将 \(?\) 替换成 \(0\) 或 \(1\) 得到的字符串，求其经过 \(k\) 次操作后序列长度之和，对 \(998244353\) 取模。
数据范围
- \(1\le n\le 10^5,1\le k\le 200\)。
时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{1024MB}\) 。
分析
对于一个已知的 \(01\) 串 \(s\) ，我们需要比模拟更快的方法求出其经过 \(k\) 次操作后的长度。
先考虑 \(k=1\) 的情况，容易发现这是将除第一段以外的每个连续段长度减一，但是可能会引起连续段合并。
这启发我们用 +1/-1 来代替 0/1 ，具体地，有以下结论：
记上一个未被删除的字符为 \(x\) ，将 \(x\) 赋值为 \(-1\) ， \(1-x\) 赋值为 \(+1\) ，如果权值到达 \(-1\)，那么下一个未被删除的字符为 \(x\)；如果权值到达 \(k+1\) ，那么下一个未被删除的字符为 \(1-x\) ，最后将权值清零。
接下来可以动态规划。
记 \(f_{i,x,j}\) 为考虑前 \(i\) 个字符，上一个未被删除的字符为 \(x\) ，当前权值为 \(j\) 的序列个数与长度之和，用二元组存储。
对于普通转移，我们只需要让序列个数和权值之和分别相加即可；对于涉及到新字符的转移，原先的每个序列都会产生 \(1\) 的贡献，将前者的序列个数加到后者的长度之和中即可。
时间复杂度 \(\mathcal O(nk)\)。
#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=1e5+5,mod=998244353;
int k,n,res;
char s[maxn];
pii f[2][2][205];
void add(int &a,int b)
{
if((a+=b)>=mod) a-=mod;
}
void tran(pii &a,pii &b,bool op)
{
add(b.fi,a.fi),add(b.se,a.se);
if(op) add(b.se,a.fi);
}
int main()
{
scanf("%d%d%s",&n,&k,s+1);
if(s[1]!='1') f[1][0][0]=mp(1,1);
if(s[1]!='0') f[1][1][0]=mp(1,1);
for(int i=2;i<=n;i++)
{
memset(f[i&1],0,sizeof(f[i&1]));
for(int x=0;x<=1;x++)
for(int j=0;j<=k;j++)
{
pii &v=f[i-1&1][x][j];
if(!v.fi&&!v.se) continue;
if(s[i]-'0'!=(x^1)) j>0?tran(v,f[i&1][x][j-1],0):tran(v,f[i&1][x][0],1);
if(s[i]-'0'!=x) j<k?tran(v,f[i&1][x][j+1],0):tran(v,f[i&1][x^1][0],1);
}
}
for(int x=0;x<=1;x++) for(int j=0;j<=k;j++) add(res,f[n&1][x][j].se);
printf("%d\n",res);
return 0;
}
uoj891 难度查找
题目描述
本题是交互题。
给定 \(k\) 和 \(n\times n\) 的矩阵 \(a\) ，保证 \(a_{i,j}\le a_{i,j+1},a_{i,j}\le a_{i+1,j}\) 。
你可以调用以下函数：
-
long long query(int x,int y);该函数返回 \(a_{x,y}\) 的值，你可以调用不超过 \(10^6\) 次。
你需要实现以下函数：
-
long long solve(int n,long long k);该函数返回矩阵 \(a\) 中第 \(k\) 小的元素。
数据范围
- \(1\le n\le 2\cdot 10^5,1\le k\le n^2,1\le a_{i,j}\le 10^{18}\)。
时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{1024MB}\) 。
分析
二分加单调栈可以做到询问次数 \(120n\) ，记录已经询问过的位置可以得到 \(40\) 分。
接下来快进到正解。
对于一个 \(n\times m\) 的矩阵，我们尝试维护由前 \(k\) 小元素构成的折线图。
具体的，记 \(p_i\) 表示第 \(i\) 列中前 \(p_i\) 个元素排在前 \(k\) 名，则 \(p_i\) 单调递减。
先求出由偶数列前 \(\lceil\frac k2\rceil\) 小元素构成的折线图（记为 \(p'_{2i}\)），令 \(p'_1=m,p'_{2i+1}=p'_{2i}\) 。
由于 \(p_i\) 单调递减，所以在上述考虑范围内的元素至少 \(2\times\lceil\frac k2\rceil\) 个，至多 \(2\times\lceil\frac k2\rceil+n\) 个。
想一想，为什么？
如果第 $2i-1$ 列只考虑前 $p'_{2i}$ 个元素，那么我们总共考虑了 $2\times\lceil\frac k2\rceil$ 个元素。 由单调性可知，在此基础上额外考虑的元素拼起来不会超过一整列，也就是 $n$ 个元素。用大根堆维护所有 \(a_{i,p'_i}\) 的值，每次弹掉最大的，直到只剩下 \(k\) 个元素，这里需要 \(n+m\) 次操作。
由于 \(m,n\) 地位相同，所以采取旋转切割的方式最优，不过需要涉及到将考虑范围从横向到纵向的转换。
不妨 \(n\ge m\) ，则操作次数满足 \(f(n,m)=f(\frac n2,m)+2m\) 。至此 \(f(n,n)\approx 6n\)，加上记忆化可以获得 \(97\) 分的好成绩。
还差最后一步优化，注意到如果 \(p_i=p_{i-1}\) ，那么第 \(i\) 列一定在第 \(i-1\) 列之前弹出。
用大根堆维护折线图的拐点，那么初始只有不超过 \(\lfloor\frac n2\rfloor\) 个拐点，即只需弹 \(\lfloor\frac n2\rfloor\) 次，每次弹出时左边和上边都可能变成了拐点。
又因为水平方向至多弹 \(m\) 次，因此 \(f(n,m)=f(\frac n2,m)+m+\frac n2\) ，解得 \(f(n,n)\approx 5n\)。
时间复杂度 \(\mathcal O(n\log n)\)。
#include<bits/stdc++.h>
#include"matrix.h"
#define ll long long
#define fi first
#define se second
#define mp make_pair
#define pii pair<ll,int>
using namespace std;
const int maxn=2e5+5;
int p[maxn],r[maxn];
unordered_map<int,ll> h[maxn];
ll get(int x,int y)
{
if(!h[x].count(y)) h[x][y]=query(x,y);
return h[x][y];
}
void work(int n,int m,ll k,int u,int v,bool rev)
{
if(m==1) return p[1]=k,void();
work(m,n/2,(k+1)/2,v,u+1,rev^1);
ll cnt=0;
for(int i=m,j=1;i>=1;i--)
{
while(j<=n/2&&p[j]>=i) j++;
r[i]=min(2*j-1,n),cnt+=r[i];
}
auto val=[&](int x,int y)
{
return !rev?get(x<<u,y<<v):get(y<<v,x<<u);
};
priority_queue<pii> q;
memcpy(p+1,r+1,4*m);
for(int i=1;i<=m;i++) if(p[i]!=p[i+1]) q.push(mp(val(p[i],i),i));
for(;cnt>k;cnt--)
{
int i=q.top().se;
q.pop();
if(p[i]==p[i-1]) q.push(mp(val(p[i],i-1),i-1));
if(--p[i]!=p[i+1]) q.push(mp(val(p[i],i),i));
}
}
ll solve(int n,ll k)
{
work(n,n,k,0,0,0);
ll res=0;
for(int i=1;i<=n;i++) if(p[i]) res=max(res,get(p[i],i));
return res;
}
uoj892 大海的深度
题目描述
给定长为 \(n\) 的数列 \(a\) ， \(m\) 次操作，每次操作将 \(a_x\) 修改为 \(w\) ，然后求 \(\sum\limits_{1\le i\le j\le n}\min\limits_{i\le k\le j}a_k\) 。
数据范围
- \(1\le n,m\le 2\cdot 10^5\) 。
- \(1\le x\le n,1\le a_i,w\le 10^6\) 。
时间限制 \(\texttt{8s}\) ，空间限制 \(\texttt{1024MB}\) 。
分析
我们在首次出现最小值的位置计算区间 \([i,j]\) 的贡献。
令 \(pre_i\) 为 \(i\) 之前第一次 \(\le a_i\) 的位置， \(suf_i\) 为 \(i\) 之后第一次 \(\lt a_i\) 的位置，则答案为 \(\sum_{i=1}^n(i-pre_i)(suf_i-i)a_i\) 。
询问分块，将涉及到的不超过 \(B\) 个位置（记为关键点）的值设为 \(\inf\) ，跑单调栈，先不统计关键点的贡献。
对于一个询问，我们需要将关键点位置改为确定的值。
先考虑 \(pre\) 改变带来的影响。关键点会将序列 \(a\) 切成 \(\mathcal O(B)\) 段，显然只有段内前缀最小值所在位置的 \(pre\) 值可能会改变。
具体的，如果对关键点和前缀 \(\min\) 做单调栈，如果跑到前缀 \(\min\) 时栈顶为关键点 \(j\) ，则 \(pre_i\to j\) ，即给答案减去 \((j-pre_i)\cdot(suf_i-i)\cdot a_i\) 。
\(suf\) 同理。我们不考虑既为前缀 \(\min\) 又为后缀 \(\min\) 的情况，因为这等价于整段 \(\min\) ，只有 \(\mathcal O(B)\) 个，用对待关键点的方法对待整段 \(\min\) 即可。
我们不可能对每次询问都暴力跑单调栈，因为前缀 \(\min\) 可能远超 \(\mathcal O(B)\) 个。但是注意到单调栈中元素是递增的，前缀 \(\min\) 是递减的。连续加入前缀 \(\min\) 的过程，其实就是对单调栈进行 pop 操作的过程。在单调栈每个元素被 pop 之前计算连续段的贡献（如果栈顶为关键点，则连续段的 \(pre\) 全部改为栈顶），复杂度就没有问题。
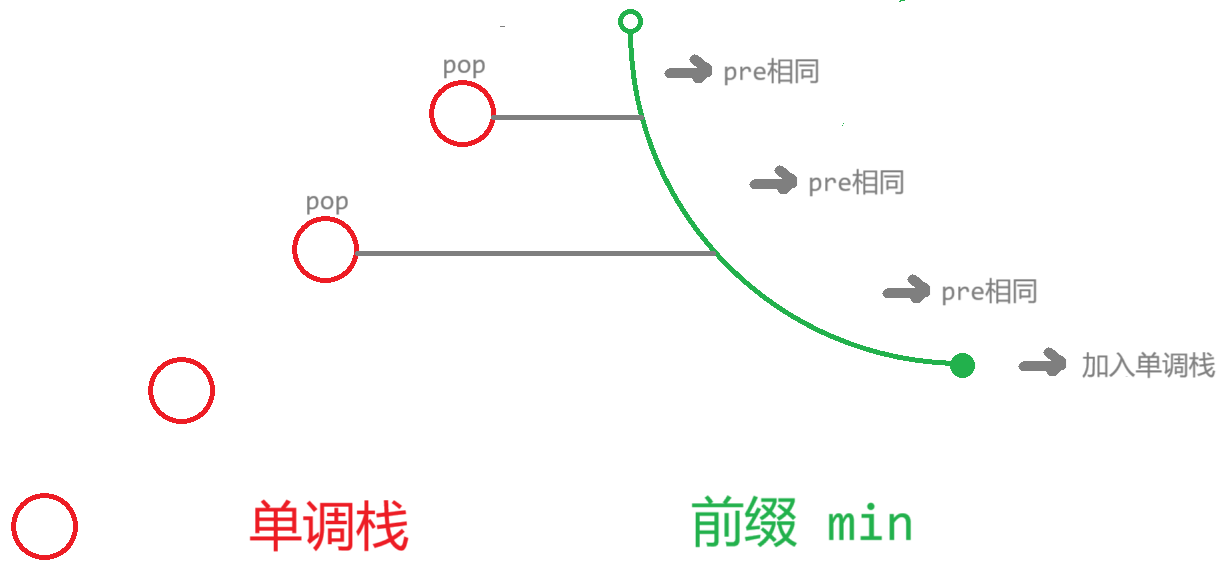
我们需要询问 "第 \(x\) 个连续段中 \(\le w_j\) 的前缀 \(\min\) 的贡献之和" ，维护成一个关于 \(j\) 的一次函数，博主代码中选择了直接二分。
再考虑 \(\mathcal O(B)\) 个关键点和整段 \(\min\) 位置的贡献。我们不能直接借用上面的单调栈，因为我们要模拟插入一个连续段而不仅仅是前缀 \(\min\) ，这可能要在单调栈中 push 很多元素。
如果考虑 \(pre\) 和 \(suf\) 限制的来源和去路，有以下 \(4\) 种情况：
- 关键点对关键点/前缀 \(\min\)：总共只有 \(\mathcal O(B)\) 个点，上面跑单调栈时顺便维护一下。
- 非关键点对前缀 \(\min\) ：预处理时已经解决。
- 非关键点对关键点：求 \(suf\) 时有用的非关键点就是全体前缀 \(\min\) ，之前的二分刚好就可以帮我们定位！
时间复杂度 \(\mathcal O(\frac{mn}B+mB\log n)=\mathcal O(m\sqrt{n\log n})\) 。
其实可以做到严格根号，由于 \(x\) 和 \(w_j\) 都只有 \(\mathcal O(B)\) 种，对每一段双指针扫前缀 \(\min\) 和 \(w_j\) ，可以做到 \(\mathcal O(n)\) 预处理， \(\mathcal O(1)\) 回答。
二分做法：link 。
下面是严格根号的代码。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define mp make_pair
#define pii pair<ll,ll>
using namespace std;
const int B=280,maxn=2e5+5,inf=1e6+5;
int m,n,cnt,top;
int a[maxn],c[maxn],st[maxn],pre[maxn],suf[maxn];
int fir[maxn],npre[maxn],nsuf[maxn];///fir为第一次出现最小值的位置
int id[inf],h1[B+5][3*B+5],h2[B+5][3*B+5];
bitset<maxn> b;
vector<int> pos;
struct modi
{
int x,w;
}o[maxn];
struct node
{
int x;
pii w;
};
vector<node> v1[B+5],v2[B+5];
pii operator+(pii a,pii b)
{
return mp(a.fi+b.fi,a.se+b.se);
}
pii operator-(pii a,pii b)
{
return mp(a.fi-b.fi,a.se-b.se);
}
pii operator*(pii a,int b)
{
return mp(a.fi*b,a.se*b);
}
ll calc(const pii &a,int x)
{
return a.fi*x+a.se;
}
void work(int l,int r)
{
b.reset(),cnt=0,pos.clear();
for(int i=l;i<=r;i++) b[o[i].x]=1,c[++cnt]=a[o[i].x],c[++cnt]=o[i].w;
st[top=0]=0;
for(int i=0;i<=n+1;i++)
{
if(!i||i==n+1||b[i]) pos.push_back(i);
else
{
while(top&&a[st[top]]>a[i]) suf[st[top--]]=i;
pre[i]=st[top],st[++top]=i;
}
}
while(top) suf[st[top--]]=n+1;
ll res=0;
for(int i=1;i<pos.size();i++)
{
int l=pos[i-1]+1,r=pos[i]-1;
fir[i]=0;
if(l>r) continue;
int c1=1,c2=1;
for(int j=l;j<=r;j++)
if(pre[j]<l&&suf[j]>r) fir[i]=j,c[++cnt]=a[j];///fir[i]的pre和suf都有可能被修改,最后单独计算它的贡献
else c1+=pre[j]<l,c2+=suf[j]>r,res+=1ll*(j-pre[j])*(suf[j]-j)*a[j];
///v1,v2分别表示前缀后缀min,x为下标,w为贡献(一次函数)
v1[i].resize(c1+1),v2[i].resize(c2+1);
v1[i][0]={0,mp(0,0)},v2[i][0]={n+1,mp(0,0)};
}
sort(c+1,c+cnt+1),cnt=unique(c+1,c+cnt+1)-c-1;
for(int i=1;i<=cnt;i++) id[c[i]]=i;
for(int i=1;i<pos.size();i++)
{
int l=pos[i-1]+1,r=pos[i]-1;
if(l>r) continue;
int c1=1,c2=1,k1=cnt,k2=cnt;
pii w1=mp(0,0),w2=mp(0,0);
///最后加入fir[i]是为了方便后面更新npre,nsuf,但不能计算fir[i]作为前缀后缀min的贡献
for(int j=l;j<=fir[i];j++)
{
if(pre[j]>=l) continue;
///h1[i][k] 最大的l满足a[v1[i][l].x]>=c[k]
if(j!=fir[i]) w1=w1+mp(1,-pre[j])*(suf[j]-j)*a[j];
v1[i][c1]={j,w1};
while(k1&&a[j]<c[k1]) h1[i][k1--]=c1-1;
c1++;
}
while(k1) h1[i][k1--]=c1-1;
for(int j=r;j>=fir[i];j--)
{
if(suf[j]<=r) continue;
///h2[i][k] 最大的l满足a[v2[i][l].x]>c[k]
if(j!=fir[i]) w2=w2+mp(-1,suf[j])*(j-pre[j])*a[j];
v2[i][c2]={j,w2};
while(k2&&a[j]<=c[k2]) h2[i][k2--]=c2-1;
c2++;
}
while(k2) h2[i][k2--]=c2-1;
}
for(int i=l;i<=r;i++)
{
a[o[i].x]=o[i].w,st[top=0]=0;
ll tmp=res;
///计算pre的修改
for(int j=1;j<pos.size();j++)
{
if(fir[j])
{
int x=fir[j],lst=0;
///pop
while(top&&a[st[top]]>a[x])
{
int l=h1[j][id[a[st[top]]]];
if(b[st[top]]) tmp-=calc(v1[j][l].w-v1[j][lst].w,st[top]);
nsuf[st[top--]]=v1[j][l+1].x,lst=l;
///如果栈顶为关键点,我们要将第(lst,l]个前缀min的pre修改为栈顶
///如果栈顶不为关键点,那么前缀min的pre和预处理时相比没有变化,注意并不意味着pre都是栈顶
///因为栈顶代表了一个连续段的最低点,而连续段过最低点后可以反弹变高,这对pre的影响很复杂
}
///push x
if(b[st[top]]) tmp-=calc(v1[j].back().w-v1[j][lst].w,st[top]);
st[++top]=x;
}
///push pos[j]
int x=pos[j];
while(top&&a[st[top]]>a[x]) nsuf[st[top--]]=x;
st[++top]=x;
}
///计算suf的修改
st[top=0]=n+1;
for(int j=pos.size()-1;j>=1;j--)
{
if(fir[j])
{
int x=fir[j],lst=0;
///pop
while(top&&a[st[top]]>=a[x])
{
int l=h2[j][id[a[st[top]]]];
if(b[st[top]]) tmp-=calc(v2[j][l].w-v2[j][lst].w,st[top]);
npre[st[top--]]=v2[j][l+1].x,lst=l;
}
///push x
if(b[st[top]]) tmp-=calc(v2[j].back().w-v2[j][lst].w,st[top]);
st[++top]=x;
}
///push pos[j-1]
int x=pos[j-1];
while(top&&a[st[top]]>=a[x]) npre[st[top--]]=x;
st[++top]=x;
}
///计算关键点和整段min的贡献
for(int j=1;j<pos.size();j++)
{
int x=fir[j],y=pos[j];
if(x) tmp+=1ll*(x-max(pre[x],npre[x]))*(min(suf[x],nsuf[x])-x)*a[x];
tmp+=1ll*(y-npre[y])*(nsuf[y]-y)*a[y];
}
printf("%lld\n",tmp);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d%d",&o[i].x,&o[i].w);
for(int l=1,r=B;l<=m;l+=B,r+=B) work(l,min(r,m));
return 0;
}
总结
vector的push_back可以看成超大常数 \(\mathcal O(1)\) ，不能承受 \(\mathcal O(m\sqrt{n\log n})\) 次操作，可以通过resize或reserve操作进行加速。
本文来自博客园，作者：peiwenjun，转载请注明原文链接：https://www.cnblogs.com/peiwenjun/p/18306875
