决策单调性学习笔记

目录

一、四边形不等式
定义
$\texttt{1D1D}$ 中的决策单调性
$\texttt{2D1D}$ 中的决策单调性
二、二分队列写法
三、分治写法
四、区间 $\texttt{DP}$ 写法
五、相关例题
例1、$\texttt{P1912 [NOI2009] 诗人小G}$
例2、$\texttt{LOJ6039 「雅礼集训 2017 Day5」珠宝}$
例3、$\texttt{CF868F Yet Another Minimization Problem}$
例4、$\texttt{CF1603D Artistic Partition}$
例5、$\texttt{P5892 [IOI2014]holiday 假期}$
例6、$\texttt{P4767 [IOI2000]邮局}$

一、四边形不等式

定义

如果二元函数 $w$ 满足，$\forall a\le b\le c\le d$ ，均有 $w(a,d)+w(b,c)\ge w(a,c)+w(b,d)$ ，则称 $w$ 满足四边形不等式。

结论：二元函数 $w$ 满足四边形不等式的充要条件为， $\forall a<b$ ，均有 $w(a,b+1)+w(a+1,b)\ge w(a,b)+w(a+1,b+1)$ 。

证明：

充分性显然，下面考虑必要性。

条件等价于，对于任意一个 $2\times 2$ 的正方形，左上加右下$\le$右上加左下。

目标等价于，对于任意两行两列的子矩阵，左上加右下 $\le$ 右上加左下。

将以 $(a,c),\cdots,(a,d)$ 为左上角的正方形的式子相加，可得，对于所有行以及 $c,d$ 两列构成的子矩阵，它满足四边形不等式。

在行的维度上做相同的操作即可得证。

$\texttt{1D1D}$ 中的决策单调性

对于形如 $f_i=\min\limits_{0\le j\lt i}(f_j+w_{j,i})$ 的转移方程，如果最优决策点 $p_i$ （非严格）单调递增，则称 $f$ 满足决策单调性。

注：如果有多个决策点同时达到最优，我们需要人为规定取最左或最右的决策点，但不能任取一个作为最优决策点。

结论：如果 $w$ 满足四边形不等式，则 $f$ 满足决策单调性。

证明：

反证法，假设存在 $i\lt j,p_i\gt p_j$ ，根据最优性：

$$f_{p_j}+w_{p_j,i}\ge f_{p_i}+w_{p_i,i}\\ f_{p_i}+w_{p_i,j}\ge f_{p_j}+w_{p_j,i}\\ $$

相加可得 $w_{p_j,i}+w_{p_i,j}\ge w_{p_i,i}+w_{p_j,j}$ 。

注意到 $p_i<i$ ，但这与四边形不等式矛盾。

如果 $f$ 的转移是 $\max$ 形式，那么四边形不等式需要反号。总而言之，四边形不等式可以简记为 "交叉优于包含" 。

划重点：如果仅有最优决策满足决策单调性，那么并不能使用下面 "二分队列" 的方法进行优化；我们需要保证对于任意两个决策点，一个前缀更优，一个后缀更优，才可以使用 "二分队列" 进行优化。

$\texttt{2D1D}$ 中的决策单调性

对于形如 $f_{l,r}=\min\limits_{l\le k\lt r}(f_{l,k}+f_{k+1,r})+w_{l,r}$ 的转移方程，如果最优决策点 $p_{l,r}$ 满足$p_{l,r-1}\le p_{l,r}\le p_{l+1,r}$，则称 $f$ 满足决策单调性。

结论：如果 $w$ 满足下述条件，则 $f$ 满足四边形不等式和决策单调性。

• $w$ 满足四边形不等式。
• $\forall i,w_{i,i}=0$。
• $\forall a\le b\le c\le d,w_{a,d}\ge w_{b,c}$。

证明过于繁琐，懒得写了。甩个链接，想看的自己去看。

---

由于某些显而易见的原因，本文例题部分不会严谨证明转移矩阵满足四边形不等式。

在实际操作中，如果你认为某个 $\texttt{dp}$ 方程可以用决策单调性优化，不妨通过打表判断决策点是否单调来验证你的猜想。

二、二分队列写法

适用范围：绝大多数 $\texttt{1D1D}$ 决策单调性优化。

转移方程：$f_i=\min\limits_{0\le j\lt i}(f_j+w_{j,i})$，其中 $w_{j,i}$ 满足四边形不等式。

二分队列的主要思想是对每个 $i$ ，维护其最优决策 $p_i$ 的值。

每计算出一个 $f_i$ ，它可以作为决策点去更新后面的 $f$ 值。根据决策单调性，$i$ 仅可能作为一个后缀的最优决策（注意当前已有的决策点只有 $1\sim i$ ）。

具体实现时，用一个单调队列维护三元组 {x,l,r} ，表示决策点 $x$ 是区间 $[l,r]$ 的最优决策点。

在插入一个点 $i$ 时，倒序枚举每个三元组，如果对于左端点 $l$ ，满足最优决策点不再是原来的决策点 $x$ （而变为当前点 $i$ ），根据决策单调性，整个区间的最优决策点都会变成 $i$ ，从而可以把这个区间删去。

如果对于左端点 $l$ ，最优决策点并没有发生变化，由于需要变成i的位置是一段后缀，在区间内二分即可。

时间复杂度$\mathcal O(n\log n)$。

struct node
{
    int x,l,r;
}q[maxn];///单调队列
int calc(int j,int i)
{///j向i的转移代价,保证j<i
    return f[j]+w(j,i);
}
int main()
{
    q[h=t=1]={0,1,n};///初始所有位置的最优决策点均为0
    for(int i=1;i<=n;i++)
    {
        while(h<t&&q[h].r<i) h++;///删掉已经过时的决策点,注意一定不会删空
        f[i]=calc(q[h].x,i);///更新f[i]的值
        while(h<t&&calc(i,q[t].l)<=calc(q[t].x,q[t].l)) t--;///如果从i转移比从原先的决策点优,删掉这个区间
        int l=max(i,q[t].l-1),r=q[t].r+1;///二分有效区间(l,r],如果i对整个区间都不优返回q[t].r+1
        ///注意calc函数在j>=i时可能无定义,所以需要保证l>=i
        while(r-l>1)
        {
            int mid=(l+r)/2;
            if(calc(i,mid)<=calc(q[t].x,mid)) r=mid;
            else l=mid;
        }
        if(r<=n) q[t].r=r-1,q[++t]={i,r,n};///更新队尾
    }
}

注意第16行pop时并没有把队列弹空，而是留下最后一个元素用于二分。

$\texttt{Bouns}$ ：对于另一类满足 $\forall i<j,p_i\ge p_j$ 的决策单调性，可以用 "二分栈" 实现，具体可见例题柠檬。

三、分治写法

适用范围： $i\to j$ 的转移不依赖于 $f_i$ ，常见于分层的 $\texttt{1D1D}$ 转移。

转移方程： $f_i=\min\limits_{1\le j\le n}(g_j+w_{j,i})$ 。

向下递归分治，假设当前正在处理 $f_l\sim f_r$ 的值，已知 $p_l\ge L,p_r\le R$ 。

记 $mid=\frac{l+r}2$ ，根据决策单调性， $L\le p_{mid}\le R$ 。

先暴力扫描区间 $[L,R]$ ，求出 $f_{mid}$ 和 $p_{mid}$ 的值，再分别递归两侧即可。

每向下递归一层区间 $[l,r]$ 长度会减半，因此至多只会递归 $\mathcal O(\log n)$ 层。

每层 $\sum(r-l)=\sum(R-L)=\mathcal O(n)$ ，时间复杂度为$O(n\log n)$。

int calc(int j,int i)
{///上一层j向当前层i的转移代价,不一定需要j<i
    return g[j]+w(j,i);
}
void solve(int l,int r,int L,int R)
{///正在计算f[l~r],保证最优决策点包含[L,R]
    if(l>r) return ;
    int mid=(l+r)/2,pos=0,val=inf;
    for(int i=L;i<=R;i++)
        if(calc(mid,i)<val)
            pos=i,val=calc(mid,i);
    f[mid]=val;///暴力求出f[mid]的值,最优决策点为pos
    solve(l,mid-1,L,pos);
    solve(mid+1,r,pos,R);
}

如果保证 $p_i<i$ ，也可以用 "二分队列" 实现。

如果 $j\le i$ 时 calc 函数无定义，需要返回 inf 。当分治递归到 r<=i 的区间时 f[mid]=inf,pos=0 ，但分治可以正常进行，无需特殊处理。

---

小技巧：如果 $w(l,r)$ 不能 $\mathcal O(1)$ 计算，但是可以 $\mathcal O(1)$ 从 $w(l\pm 1,r)$ 和 $w(l,r\pm 1)$ 递推得到，我们可以用类似莫队的方式移动指针处理。

证明：

对于右端点，单次移动次数和 $r-l$ 同阶。

对于左端点，单次移动次数和 $R-L$ 同阶。

时间复杂度 $\mathcal O\big(\sum(r-l+R-L)\cdot\log n\big)=\mathcal O(n\log n)$。

四、区间 $\texttt{DP}$ 写法

适用范围：一般用于优化 $\texttt{2D1D}$ 型 $\texttt{DP}$ 。

转移方程：$f_{l,r}=\min\limits_{l\le k\lt r}\big(f_{l,k}+f_{k+1,r}+w_{l,r}\big)$ 。

记录最优决策点 $p_{l,r}$ ，暴力枚举 $[p_{l,r-1},p_{l+1,r}]$ 范围内的所有决策点即可。

时间复杂度 $\mathcal O(n^2)$ ，证明如下：

计算 $f_{l,r}$ 的答案时，枚举量为 $p_{l+1,r}-p_{l,r-1}$ 。

放在二维矩阵上看，相当于 $f_{l,r}$ 给下边的格子贡献系数 $1$ ，给左边的格子贡献系数 $-1$ ，总代价为所有格子的系数乘以 $p_{l,r}$ 之和。

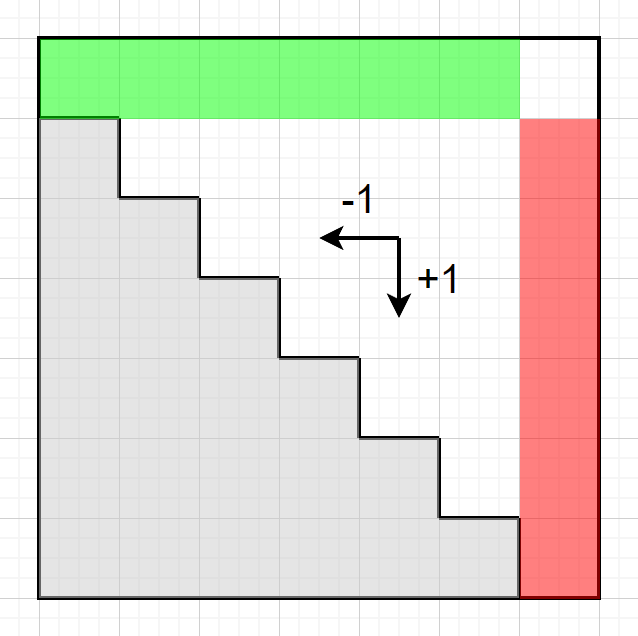
如上图，灰色是不合法的格子，有且仅有红色格子系数为 +1 ，绿色格子系数为 -1 。

时间复杂度为 $\mathcal O(\sum p_{i,n}-\sum p_{1,i})=\mathcal O(n^2)$ 。

代码非常好写：

for(int i=1;i<=n;i++) f[i][i]=w(i,i),p[i][i]=i;
for(int len=2;len<=n;len++)///区间长度从2开始枚举
    for(int l=1,r=len;r<=n;l++,r++)
    {
        f[l][r]=inf;
        for(int k=p[l][r-1];k<=p[l+1][r];k++)
            if(f[l][k]+f[k+1][r]+w(l,r)<=f[l][r])
                f[l][r]=f[l][k]+f[k+1][r]+w(l,r),p[l][r]=k;
    }

五、相关例题

例1、$\texttt{P1912 [NOI2009] 诗人小G}$

题目描述

$T$ 组数据，给定 $n$ 个句子，行标准长度为 $l$ 。每一行可以放若干个连续的句子，相邻两个句子之间需要一个空格。

每一行的不协调度为该行实际长度与 $l$ 之差的绝对值的 $p$ 次方，求所有行的不协调度的最小值。

数据范围

• $1\le T\le 10,1\le n\le 10^5,1\le l\le 3\cdot 10^6,1\le p\le 10$ 。
• 句子长度 $\le 30$ 。

时间限制 $\texttt{2s}$ ，空间限制 $\texttt{250MB}$ 。

分析

记句子长度前缀和为 $s_i$ ，写下前 $i$ 个句子的最小不协调度为 $f_i$ ，转移方程为：

$$f_i=\min_{0\le j<i}\big(f_j+|s_i-s_j+i-j-1-l|^p\big)$$

打表可知，$w_{j,i}=|s_i-s_j+i-j-1|^p$满足四边形不等式，用二分栈实现。

注意本题答案会爆 long long ，所以需要用 long double 存储 $\texttt{dp}$ 数组，通过牺牲精度的方式换取更大的值域。

时间复杂度 $\mathcal O(Tn\log n)$。

#include<bits/stdc++.h>
#define ld long double
using namespace std;
const int maxn=1e5+5;
int h,l,n,p,t,cas;
char ch[maxn][35];
int s[maxn],pos[maxn];
ld f[maxn];
struct node
{
    int x,l,r;
}q[maxn];
ld qpow(ld a,int k)
{
    ld res=1;
    for(int i=1;i<=k;i++) res*=a;
    return res;
}
ld calc(int j,int i)
{
    return f[j]+qpow(abs(s[i]-s[j]+i-j-1-l),p);
}
void print(int n)
{
    if(!n) return ;
    print(pos[n]);
    for(int i=pos[n]+1;i<=n;i++) printf("%s%c",ch[i]+1,i!=n?' ':'\n');
}
int main()
{
    scanf("%d",&cas);
    while(cas--)
    {
        scanf("%d%d%d",&n,&l,&p);
        for(int i=1;i<=n;i++)
        {
            scanf("%s",ch[i]+1);
            s[i]=s[i-1]+strlen(ch[i]+1);
        }
        q[h=t=1]={0,1,n};
        for(int i=1;i<=n;i++)
        {
            while(h<t&&q[h].r<i) h++;
            f[i]=calc(q[h].x,i),pos[i]=q[h].x;///记录最优决策点,用于输出方案
            while(h<t&&calc(i,q[t].l)<calc(q[t].x,q[t].l)) t--;
            int l=q[t].l-1,r=q[t].r+1;
            while(r-l>1)
            {
                int mid=(l+r)/2;
                if(calc(i,mid)<calc(q[t].x,mid)) r=mid;
                else l=mid;
            }
            if(r<=n) q[t].r=r-1,q[++t]={i,r,n};
        }
        if(f[n]<=1e18) printf("%.0Lf\n",f[n]),print(n);
        else printf("Too hard to arrange\n");
        printf("--------------------\n");
    }
    return 0;
}

例2、$\texttt{LOJ6039 「雅礼集训 2017 Day5」珠宝}$

题目描述

有 $n$ 种珠宝，第 $i$ 种的价格为 $c_i$ 元，吸引力为 $v_i$ 。

对 $\forall 1\le i\le k$ ，假如你可以支付不超过 $i$ 元，求吸引力之和的最大值。

数据范围

• $1\le n\le 10^6,1\le k\le 5\cdot 10^4,1\le c_i\le 300,0\le v_i\le 10^9$ 。

时间限制 $\texttt{2s}$ ，空间限制 $\texttt{256MB}$ 。

分析

普通背包的时间复杂度为 $\mathcal O(nk)$ ，肯定过不了。

但是单个物品的价格很小，这启示我们重新设计状态。

将所有价格相同的物品按吸引力降序排序，显然只会取一个前缀，记前缀和为 $s_k$ 。

$f_{i,j}$ 表示考虑所有价格 $\le i$ 的物品，总价格为 $j$ ，吸引力之和的最大值。转移方程为：

$$f_{i,j}=\max_{0\le c\cdot k\le j}\big(f_{i,j-c\cdot k}+s_k\big)$$

下标按照 $\bmod c$ 分类，转移矩阵 $w(i,j)=s_{j-i}$ ，满足决策单调性。

关于本题 $w(i,j)$ 的决策单调性的感性理解： "交叉" 和 "包含" 选择的物品个数是相同的，但 "交叉" 取的物品吸引力更大，所以更优。

对每个 $\bmod c$ 的剩余系分别用决策单调性优化即可。

时间复杂度 $\mathcal O(300\cdot k\log k)$ 。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=5e4+5;
int c,k,n,v;
ll f[maxn],g[maxn],s[maxn],dp[maxn];
vector<int> vec[maxn];
void solve(int l,int r,int L,int R)
{
    if(l>r) return ;
    int mid=(l+r)/2,pos=0;
    ll val=-1e18;
    for(int i=L;i<=R&&i<=mid;i++)///i>mid时不能转移,可以认为w(i,mid)=-inf
        if(g[i]+s[mid-i]>val)
            val=g[i]+s[mid-i],pos=i;
    f[mid]=val;
    solve(l,mid-1,L,pos);
    solve(mid+1,r,pos,R);
}
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++) scanf("%d%d",&c,&v),vec[c].push_back(v);
    for(int i=1;i<=300;i++)
    {
        if(vec[i].empty()) continue;
        sort(vec[i].begin(),vec[i].end(),greater<int>());
        int l=vec[i].size();
        for(int j=1;j<=k/i;j++) s[j]=j<=l?s[j-1]+vec[i][j-1]:0;
        for(int r=0;r<i;r++)
        {
            int m=0;
            for(int j=r;j<=k;j+=i) g[++m]=dp[j];
            solve(1,m,1,m);
            for(int j=r;j<=k;j+=i) dp[j]=f[j/i+1];
        }
    }
    for(int i=1;i<=k;i++) printf("%lld ",dp[i]);
    putchar('\n');
    return 0;
}

例3、$\texttt{CF868F Yet Another Minimization Problem}$

同类题$\texttt{P5574 [CmdOI2019]任务分配问题}$。

题目描述

给定长为 $n$ 的序列 $a$ ，要求分成 $k$ 段，每段代价为 $\sum_{l\le i\lt j\le r}[a_i=a_j]$ 。

求所有划分方案中，代价之和的最小值。

数据范围

• $2\le n\le 10^5,2\le k\le\min(n,20),1\le a_i\le n$ 。

时间限制 $\texttt{2s}$ ，空间限制 $\texttt{256MB}$ 。

分析

$f_{i,j}$ 表示将 $[1,j]$ 划分为 $i$ 段，代价之和的最小值。转移方程为：

$$f_{i,j}=\min_{0\le k<j}\big(f_{i-1,k}+w_{k+1,j}\big)$$

其中 $w(l,r)$ 为区间 $[l,r]$ 中相等元素的对数，满足四边形不等式。

注意 $w$ 不能 $\mathcal O(1)$ 计算，需要用莫队维护指针的方式处理。

时间复杂度 $\mathcal O(kn\log n)$ 。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+5,inf=1e18;
int k,l=1,n,r,sum;
int a[maxn],cnt[maxn];
int f[25][maxn];
void add(int x)
{
    sum+=cnt[a[x]]++;
}
void del(int x)
{
    sum-=--cnt[a[x]];
}
int calc(int L,int R)
{
    while(l>L) add(--l);
    while(r<R) add(++r);
    while(l<L) del(l++);
    while(r>R) del(r--);
    return sum;
}
void solve(int i,int l,int r,int L,int R)
{
    if(l>r) return ;
    int mid=(l+r)/2,pos=0,val=inf;
    for(int j=L;j<=R&&j<mid;j++)
        if(f[i-1][j]+calc(j+1,mid)<=val)
            val=f[i-1][j]+calc(j+1,mid),pos=j;
    f[i][mid]=val;
    solve(i,l,mid-1,L,pos);
    solve(i,mid+1,r,pos,R);
}
signed main()
{
    scanf("%lld%lld",&n,&k);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    for(int i=0;i<=k;i++) for(int j=0;j<=n;j++) f[i][j]=inf;
    f[0][0]=0;
    for(int i=1;i<=k;i++) solve(i,0,n,0,n);
    printf("%lld\n",f[k][n]);
    return 0;
}

注意执行到第 $31$ 行时 pos 可能为零，这意味着 f[i][mid] 是一个不合法的状态（ mid<i ）。

此时不需要手动 return ，因为区间内其他f值可能还没被算到，但是更稳妥的方法是在第 $27$ 行赋初始值 pos=L （或 $[L,R]$ 内任何一个数）。

例4、$\texttt{CF1603D Artistic Partition}$

题目描述

定义 $c(l,r)=\sum\limits_{l\le i\le j\le r}[\gcd(i,j)\ge l]$ 。

$T$ 组数据，给定 $n,k$ ，求$\min\limits_{0=x_1\lt\cdots\lt x_{k+1}=n}\sum_{i=1}^kc(x_i,x_{i+1})$。

数据范围

• $1\le T\le 3\cdot 10^5,1\le k\le n\le 10^5$ 。

时间限制 $\texttt{3s}$ ，空间限制 $\texttt{1024MB}$ 。

分析

容易想到动态规划， $f_{i,j}$ 表示将 $[1,j]$ 划分成 $i$ 段，代价之和的最小值。

乍一看状态数 $\mathcal O(n^2)$ ，但是注意到 $c(l,r)\ge r-l+1$ ，并且 $c(l,l)=1$ ，因此当 $n\le 2^k-1$ 时，答案一定为 $n$ 。

于是第一维上界变成 $\log n$ ，总状态数 $\mathcal O(n\log n)$ 可以接受。

转移方程如下：

$$f_{i,j}=\min_{0\le k\lt j}\big(f_{i-1,k}+c(k+1,j)\big)$$

先把 $c(l,r)$ 化简一下：

$$\sum_{l\le i\le j\le r}[\gcd(i,j)\ge l]\\ =\sum_{d=l}^r\sum_{l\le i\le j\le r}[\gcd(i,j)=d]\\ =\sum_{d=l}^r\sum_{1\le i\le j\le\lfloor\frac rd\rfloor}[\gcd(i,j)=1]\\ =\sum_{d=l}^r\sum_{j=1}^{\lfloor\frac rd\rfloor}\varphi(j)$$

预处理 $\varphi$ 的前缀和，单次计算$c$可以用整除分块优化到 $O(\sqrt{r-l})$ 。

发现 $c$ 满足四边形不等式。在分治暴力寻找决策点时，由于$r$固定，所以可以从 $c(l,r)$ 直接递推得到 $c(l-1,r)$ 的值。

求出整个 $\texttt{dp}$ 数组后可以 $\mathcal O(1)$ 回答询问，时间复杂度 $O(n\log^2n+T)$ 。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+5,inf=1e18;
int k,n,t;
int b[maxn],p[maxn],s[maxn],phi[maxn];
int f[18][maxn];
int calc(int x,int y)
{
    int res=0;
    for(int l=x,r=0;l<=y;l=r+1) r=y/(y/l),res+=(r-l+1)*s[y/l];
    return res;
}
void solve(int i,int l,int r,int L,int R)
{
    if(l>r) return ;
    int mid=(l+r)/2,pos=0,val=inf;
    for(int j=min(mid,R),now=calc(j+1,mid);j>=L;j--)
    {
        if(f[i-1][j]+now<val) val=f[i-1][j]+now,pos=j;
        now+=s[mid/j];
    }
    f[i][mid]=val;
    solve(i,l,mid-1,L,pos);
    solve(i,mid+1,r,pos,R);
}
void init(int n)
{
    phi[1]=1;
    for(int i=2,cnt=0;i<=n;i++)
    {
        if(!b[i]) p[++cnt]=i,phi[i]=i-1;
        for(int j=1;j<=cnt&&i*p[j]<=n;j++)
        {
            b[i*p[j]]=1;
            if(i%p[j]==0)
            {
                phi[i*p[j]]=phi[i]*p[j];
                break;
            }
            phi[i*p[j]]=phi[i]*phi[p[j]];
        }
    }
    for(int i=1;i<=n;i++) s[i]=s[i-1]+phi[i];
    for(int i=1;i<=n;i++) f[1][i]=i*(i+1)/2;
    for(int i=2;i<=17;i++) solve(i,1,n,1,n);
}
signed main()
{
    scanf("%lld",&t),init(maxn-5);
    while(t--)
    {
        scanf("%lld%lld",&n,&k);
        printf("%lld\n",k>=18?n:f[k][n]);
    }
    return 0;
}

例5、$\texttt{P5892 [IOI2014]holiday 假期}$

题目描述

数轴上有 $n$ 个点，第 $i$ 个点的权值为 $a_i$ 。

给定起点 $s$ ，每次操作要么移动到相邻点，要么停留在第 $i$ 个点并获得 $a_i$ 的收益，每个点至多停留一次。

求 $d$ 次操作后收益的最大值。

数据范围

• $2\le n\le 10^5,0\le d\le\lfloor\frac 52n\rfloor,0\le a_i\le 10^9$ 。

时间限制 $\texttt{1s}$ ，空间限制 $\texttt{64MB}$ 。

分析

假设我们已经确定了经过的区间 $[l,r]$ ，显然我们只会选择区间内最大的 $d-(r-l+1)-\min(s-l,r-s)$ 个点。

用可持久化线段树维护，可以做到单次 $\mathcal O(\log n)$ 计算一个区间 $[l,r]$ 的答案。

对固定的 $l$ ，记最优的决策点 $r$ 为 $p_l$ ，容易发现 $p_l$ 单调递增。

分治优化，时间复杂度 $\mathcal O(n\log^2n)$ 。

本题 $O(n\log V)$ 的空间是过不去的，需要对 $a_i$ 离散化。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+5,inf=1e9;
int d,n,s,cnt,tot;
ll res;
int a[maxn],c[maxn],rt[maxn];
struct node
{
    int ls,rs;
    ll cnt,sum;
}f[20*maxn];
void pushup(int p)
{
    f[p].cnt=f[f[p].ls].cnt+f[f[p].rs].cnt;
    f[p].sum=f[f[p].ls].sum+f[f[p].rs].sum;
}
int insert(int p,int l,int r,int pos)
{
    int q=++tot;
    f[q]=f[p];
    if(l==r)
    {
        f[q].cnt++,f[q].sum+=c[pos];
        return q;
    }
    int mid=(l+r)/2;
    if(pos<=mid) f[q].ls=insert(f[q].ls,l,mid,pos);
    else f[q].rs=insert(f[q].rs,mid+1,r,pos);
    return pushup(q),q;
}
ll query(int p,int q,int l,int r,int k)
{
    if(l==r) return 1ll*c[l]*k;
    int mid=(l+r)/2,cur=f[f[q].rs].cnt-f[f[p].rs].cnt;
    if(k<=cur) return query(f[p].rs,f[q].rs,mid+1,r,k);
    else return f[f[q].rs].sum-f[f[p].rs].sum+query(f[p].ls,f[q].ls,l,mid,k-cur);
}
ll calc(int l,int r)
{
    int w=d-(r-l)-min(s-l,r-s);
    return w<=0?0:query(rt[l-1],rt[r],1,cnt,min(w,r-l+1));
}
void solve(int l,int r,int L,int R)
{
    if(l>r) return ;
    int mid=(l+r)/2,pos=0;
    ll val=-inf;
    for(int i=L;i<=R;i++)
    {
        ll now=calc(mid,i);
        if(now>val) val=now,pos=i;
    }
    res=max(res,val);
    solve(l,mid-1,L,pos);
    solve(mid+1,r,pos,R);
}
int main()
{
    scanf("%d%d%d",&n,&s,&d),s++;
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),c[i]=a[i];
    sort(c+1,c+n+1);
    cnt=unique(c+1,c+n+1)-c-1;
    for(int i=1;i<=n;i++)
    {
        a[i]=lower_bound(c+1,c+cnt+1,a[i])-c;
        rt[i]=insert(rt[i-1],1,cnt,a[i]);
    }
    solve(1,s,s,n);
    printf("%lld\n",res);
    return 0;
}

例6、$\texttt{P4767 [IOI2000]邮局}$

题目描述

数轴上有 $n$ 个点 $a_1\lt\cdots\lt a_n$ ，你需要在数轴上选 $k$ 个点 $x_1,\cdots,x_k$ ，使得 $\sum_{i=1}^n\min\limits_{1\le j\le k}|a_i-x_j|$ 最小。

数据范围

• $1\le n\le 3000,1\le k\le\min(n,300),1\le a_i\le 10^4$ 。

时间限制 $\texttt{1s}$ ，空间限制 $\texttt{125MB}$ 。

分析

显然每个 $x_j$ 会作用于一段区间，反过来，对于一个给定的区间 $[l,r]$ ，将 $x_j$ 放在中位数位置一定最优。

$f_{i,j}$ 表示用 $j$ 个点覆盖 $a_1\sim a_i$ 的最小代价。转移方程为：

$$f_{i,j}=\min_{0\le k\lt j-1}f_{k,j-1}+w_{k+1,j}$$

其中 $w_{l,r}$ 表示选择一个 $x_j$ 覆盖区间 $[l,r]$ 的代价，可以 $O(n^2)$ 递推，也可以求前缀和后单次 $\mathcal O(1)$ 回答。

容易发现 $w$ 满足四边形不等式，用区间 $\texttt{DP}$ 写法优化即可。

如果把第二维放在前面，也可以用二分队列或者分治进行优化，但时间复杂度会多一只 $\log$ 。

边界 $f_{i,i}=0$ ，由于计算 $f_{i,j}$ 需要用到 $p_{i,j-1}$ 和 $p_{i+1,j}$ 的值，所以需要先升序枚举 $j$ ，再倒序枚举 $i$ 。

时间复杂度 $\mathcal O(kn)$ 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=3005;
int k,n;
int a[maxn],w[maxn][maxn];
int f[maxn][305],p[maxn][305];
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int len=1;len<=n;len++)
        for(int l=1,r=len;l<=n;l++,r++)
            w[l][r]=w[l+1][r-1]+a[r]-a[l];
    memset(f,0x3f,sizeof(f));
    f[0][0]=0;
    for(int j=1;j<=k;j++)
    {
        p[n+1][j]=n;
        for(int i=n;i>=1;i--)
        {
            for(int l=p[i][j-1];l<=p[i+1][j];l++)
                if(f[l][j-1]+w[l+1][i]<=f[i][j])
                    f[i][j]=f[l][j-1]+w[l+1][i],p[i][j]=l;
        }
    }
    printf("%d\n",f[n][k]);
    return 0;
}