数据结构--树
树和二叉树的定义
树的基本术语
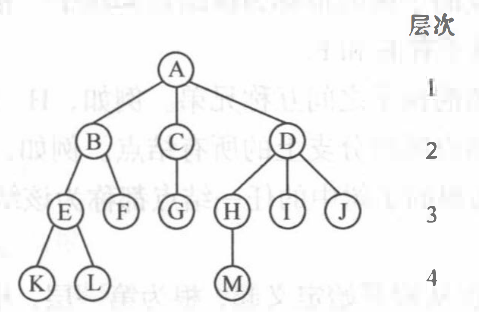
- 结点:树中的每一个独立单元。如图中的A、B、C、D等。
- 结点的度:结点拥有的子树的个数称为结点的度。
- 树的度:树内各节点度的最大值。
- 叶子:度为0的结点称为叶子节点。如图中的K 、 L 、 F 、 G 、 M 、 I 、 J。
- 非终端节点:度不为0的结点。
- 双亲和孩子:结点的子树的根称为该结点的孩子,该结点称为孩子的双亲。
- 兄弟:双亲相同的两个结点。
- 祖先:从根到该结点所经分支上的所有结点。
- 子孙:以某结点为根的子树中的任一结点都称为该结点的子孙。
- 层次:根结点为第一层,气候没多一层层数加1。
- 堂兄弟:双亲在同 一层的结点互为堂兄弟。
- 树的深度:树中结点的最大层次称为树的深度或高度。
二叉树的定义
二叉树是n(n≥0)个结点所构成的集合,当n=0时称为空树,对于非空树T:
- 有且仅有一个根结点
- 每个根结点最多只能有两个孩子。
二叉树
满二叉树和完全二叉树
满二叉树

深度为k且含有2k - 1个结点的二叉树。
完全二叉树

深度为k的,有n个结点的二叉树,其每一个结点都遵循从左到右的顺序进行编号,不存在间断,则称之为完全二叉树。
二叉树的性质
性质一
在二叉树的第i层上最多有2i-1个结点(i≥1)。
性质二
深度为k的二叉树最多有2k-1个结点(k≥1)。
性质三
对任何一棵二叉树T,如果其终端结点树为n0,度为2的节点数为n2,则n0 = n2 + 1
性质四
具有n个结点的完全二叉树的深度为⌊log2n⌋ + 1。
性质五
如果对一棵有n个结点的完全二叉树(其深度为⌊log2n⌋ + 1)的结点按层序编号,则对任一节点i(1 ≤ i ≤ n),有
- 如果i = 1,则结点i是二叉树的根,无双亲;如果i > 1,则其双亲是结点⌊i/2⌋
- 如果2i > n,则结点i无左孩子(结点i为叶子节点);否则其左孩子是结点2i
- 如果2i + 1 > n,则结点无右孩子;否则其右孩子是结点2i + 1
二叉树的遍历
遍历二叉树是指按某条搜索路径巡防树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。
二叉树的先序遍历
先访问根节点,先序遍历左子树,先序遍历右子树。
二叉树的中序遍历
先中序遍历左子树,访问根节点,中序遍历右子树
二叉树的后序遍历
先后序遍历左子树,后序遍历右子树,访问根节点。

