在贝叶斯框架中,一个完成训练的神经网络是通过其权重的后验概率来表达的。当给网络一个输入数据时,权重分布产生网络输出的分布。同时,对输为的所做的高斯噪声假定也会影响网络输出的分布。这里,通过前面介绍的单高斯近似来计算输出的分布。
输出的分布为
要计算上面的分布,需要利用两个东东:
1)权重后验概率分布:前面介绍过通过利用高斯分布来近似此分布
从而得到输出的分布为:
进一步假设此后验概率分布足够窄(由矩阵A决定),这样就可以通过在![]() 进行线性扩展来近似
进行线性扩展来近似![]() ,得到:
,得到:
这样,就可将式(1)写成
上式积分的结果恰恰是高斯分布:
通过对式(4)的分析,可以洞察到以下东西:
1)对于t的预测分布的标准差
可看作平均值
的误差条(an error bar)
2)有两个东西对误差条有贡献:
a)目标数据的内部噪声
,对应于第一项
。当噪声很大时,
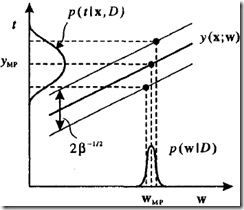
小,噪声项起绝对作用,如下面左图所示
b)网络权重后验概率分布
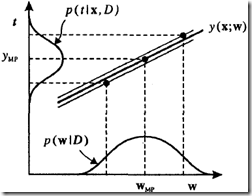
的宽度,对应于第二项。当噪声小时,此后验的方差起绝对作用。
到此,越发佩服贝叶斯技术了吧,它不仅给出一个最佳的预测输出,同时给出输出的误差条。实践中,可以利用两步来计算此误差条:
2)计算赫森阵A,带入式(5),得到误差条
1.贝叶斯回归案例
考虑一个单输入-单输出的例子:
1)30个数据点,生成自
,附带标准差为0.05的高斯加性噪声
2)x抽样自a Gaussian mixture distribution having two wellseparated components
3)采用多参感知器,隐藏4个神经元,激励函数为tanh
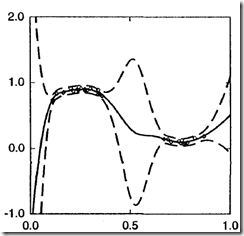
利用前面介绍的误差条计算方法可以生成如下图形,其中实线为权重![]() 对应网络的输出,虚线为
对应网络的输出,虚线为![]() (利用式5计算)误差。
(利用式5计算)误差。
注意:输入空间中数据密度低的地方,误差条较宽
2.广义线性网络
对于单层网络,当输出单元是线性时,网络映射是权重的线性函数。这样的模型可表达为 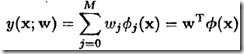


 浙公网安备 33010602011771号
浙公网安备 33010602011771号