7.4 DFT窗效应
当研究的是时不变信号时,若采样频率一定,则用长的窗可给出更准确的频谱;若信号为时变的,则长的窗可能会使结果发生混淆。
1)时域采样频率一定,短窗意味着采样点少,响应频域采样点也少,造成频率分辨率fs/N变差;反之,长窗则频率采样点多,频率分辨率变好
2)但是,使用长窗的DFT不能提供单个信号的频谱特性。对语言来说,为了揭示某个元音的频率,窗的长度不能超过它的持续时间,因为更宽的窗不仅捕捉该元音,也捕捉临近声音的频率。
窗长度的选择要同时考虑时域和频率的需求。
1)采样速率一定,DFT要分析时域小的细节(如单个元音),就要用窄的窗,代价就是频率分辨率变差
2)要改善频率分辨率,时域就要用宽的窗,代价就是DFT反映单频率分量的能力变差
窗长度可变是DFT的优点,使得它即可描述细节部分,也可描述大的部分。
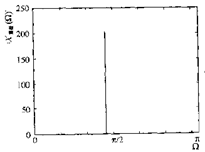
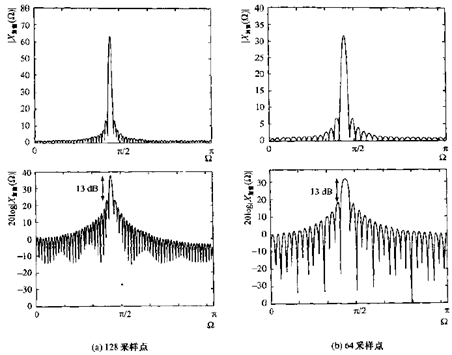
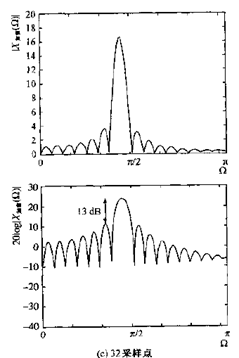
加窗是DFT误差的主要来源之一,下面通过图示来说明(这里采样DTFT,应为它能更清晰反映窗形状变化的影响)。
2)对于频率特性不随时间变化的信号,窗越长,DFT分辨率改善,正弦频谱的峰变窄,对原信号频谱的近似越好,
7.5 频谱图
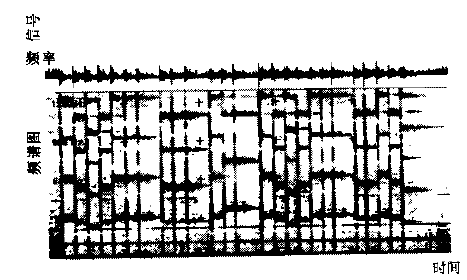
DFT分析的关键是选择窗的长度,使之适合待分析的信号。单个DFT只能提供信号的有限信息,而DFT集合(每个给出不同时间间隔的信号)更有帮助。频谱图是描绘DFT集合的图形,横坐标为时间,纵坐标为频率,每个竖段是DFT幅度频谱(幅度越多颜色越深)。
下图是“Mary had a little lamb”的频谱图和乐谱(乐谱也是一种时频图)。
7.6 FFT
快速傅里叶变换(fast Fourier transform, FFT)的输出与DFT相同,但运输量要小的多。最常用的FFT是基2时域抽取法FFT(radix-2 decimation-in-time FFT),它的基本原理是将一个N点的计算分解为两个N/2点的计算,每个N/2点的计算再分解为N/4点的计算。
推导过程如下
2)上式两项具有DFT的形式,可写为
其中:Y[k]是偶采样点的DFT,Z[k]是奇采样点的DFT,乘数
是旋转因子
3)上式可进一步分解为两个N/2d点的DFT
由于Y[k]和Z[k]的周期为N/2,上式改写为
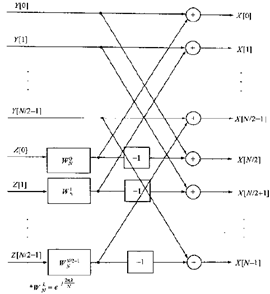
由式(1)和(2)构成的DFT1级计算示意图如下
一个8点FFT的所有三级运算如下图
对比分析FFT和DFT的运算效率
1)DFT中对每个点要计算N次乘法以及(N-1)次加法,对于N个点则要计算N*N次乘法以及N*(N-1)次加法,时间复杂度为N*N
2)FFT的每一级有N次乘法以及N次加法,FFT共有
级,时间复杂度为
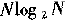
7.7 2维DFT和FFT
对于图形等2维信号也需要分析频谱特性,2维DFT其实是1维DFT的自然延展,公式如下
其实,2维计算就是就是现在图像的每一行上进行1维DFT计算,然后在此矩阵的列上再进行1维DFT计算。



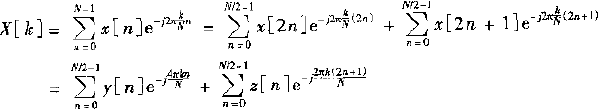
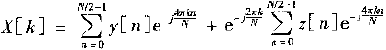

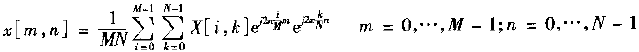

 浙公网安备 33010602011771号
浙公网安备 33010602011771号