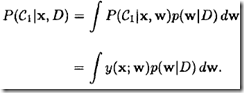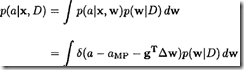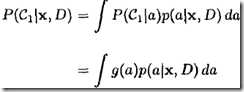考虑两类问题。数据的似然函数为
（1），G是交叉熵误差函数
选择logistic sigmoid为输出激励函数
，
。这种激励函数可将网络输出解释为x属于类的概率
。
然后同前面一样，贝叶斯框架下对分类问题处理步骤也是三步：
1）权重先验：基于正则化项
引入网络权重先验
2）权重的后验：基于1）可推出
，同样可以通过中心在
的单高斯分布近似
（2）
3）输出的分布：x属于类C1的概率通过对权重分布的积分得到
（3）
但是分类和回归问题中处理细节稍有不同：
1）回归问题：网络输出是均值为
的高斯分布，这样式（3）的预测结果就等于直接采用
2）分类问题：由于采用sigmoid为输出激励函数，因此无法将y近似为权重W的线性函数。
由于上面的区别，在分类中，按式（2）进行积分时需要进行重要变化。具体有哪些变化呢？
1）因为y无法近似处理，所以要摆弄的对象就变了。MacKay (1992b)假设a（而不是y）是一个关于权重的局部线性函数
，
a的分布为
2）权重后验概率采用式（2）。因为
要求
与a是线性的，且权重后验是高斯的，因此a的分布也是高斯分布
，
3）从而得到
（4）
4）由于式（4）无解析解，MacKay (1992b)建议采用下面的近似
，
，
到这里，学到两中分类方法
1）通过式4积分得到的分类结果，
2）通过取权重为某一固定值时，直接进行分类。如取权重为
关键是需要进一步思考这两种方法有什么本质区别。Show图来点直观的感受吧。
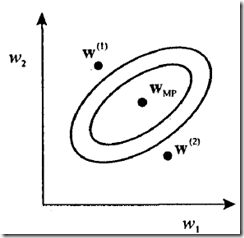
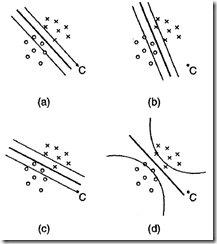
图1:权重后验概率分布示意图 图2：单层、输出为logistic sigmoid函数神经网络的输出等高线（同条线上输出相同）
1）图2-(a)：对应采用分类方法2，且中权重为图1中
2）图2-(b和c)：对应采用分类方法2，且中权重为图1中权重为W1和W2网络的决策面。注意，此时点C被分为不同类别。
3）图2-(d)：对应采用分类方法1，通过对整个权重空间积分进行分类。注意，等高线在数据点少的地方向远处延伸，且此时点C赋给某类概率值为0.5（这才是所期望的结果）
4）图2中d和c图中决策边界（对应中间y=0.5的那条线）是相同的
