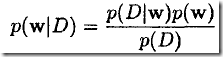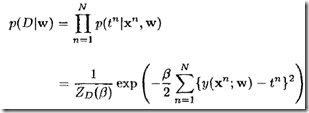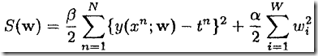这里虽然探讨ANN的权重贝叶斯学习，我们完全可以将其看做是任意模型的参数学习问题。
最大似然（误差最小）获得网络权重的一个解（一个权重向量）。而贝叶斯方法考虑的权重空间（即权重的整个解空间上许多解）上权重的概率分布，通过先验概论表达不同权重值的相对置信度。当越来越多的数据观测到，权重的后验概率会逐渐集中到权重空间的局部上。
1.权重的分布
对结构确定的神经网络，其权重
在未给定任何数据时的先验概率为
；当给的训练数据
后，其后验概率为：
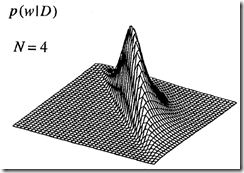
当观测到更多数据时，后验概率会逐步收缩，如下图。这说明已学习到一些关于权重与观测到的数据是否相符方面的信息。
WMp对应后验概率的最大值，实际上后验概率形式比较复杂，会有多个局部最大值。
2.高斯先验（Gaussian Prior）
首先摆弄一下权重的先验。它应该能表达我们关于期望获得的网络映射（即神经网络对应的映射函数）的先验知识。一般，权重的先验先验分布可写成指数形式 
。同时，考虑到光滑网络映射的泛化能力更好，且可通过小网络权重值获得。因而，取
（这是正则化技术的动机之一） 。
其实，上面的技术可用高斯分布（0处概率最大，值越大概率越小）表达，即构造如下先验。
其中，参数
是超参数（hyperparameter），它控制着其它参数（权重和偏置）的分布，这里假设其值已知。
还有许多先验可用，相关参考文献：
1）Laplacian prior，Williams (1995)
2）entropy-based priors，Buntine and Weigend (1991)
3）The appropriate selection of priors for very large networks，Neal (1994)
3.贝叶斯学习实例
以一个简单的用于分类的单层网络为例：
1）权重
，
＝1
2）输出为logistic函数
3）训练数据：2维，4条数据（分别有2条属于类1和类2）
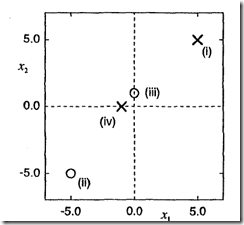
圈和叉分别代表两类数据，编号(I,II等）代表数据用于训练网络时的顺序
下面，通过几个图来看看权重的先验，以及后验随不断观测到新数据后是如和变化的。
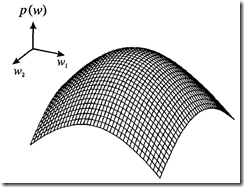
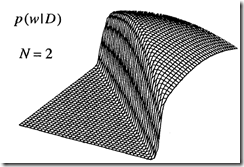
图1. 权重的高斯先验分布 图2.数据1和2参与训练后权重的后验分布 图3.所以4条数据都参与训练后权重的后验分布
通过观察这3张图，可看出如下门道：
1）神经网络输出采用logistic函数，权重w1和w2会影响并控制整个网络所代表的分类判别函数的形状
2）图2：数据I和数据II使一半权重空间上权重的后验概率值非常小，因为这些权重会使得决策面的朝向错误方向；权重空间其它部分的后验概率基本没有变化，保留了先验分布。
3）图3：当4条数据都参与训练后，由于没有决策面能非常完美对其分类，最可能解的对应与具有特殊形状的决策面。因此，仅有很窄的区域权重的后验概率较大，大部分区域都非常小。
4.高斯噪声模型
下面来看一个结构更一般的针对回归问题的前向神经网络。一般，权重的似然函数为
，
其中，
为误差函数，
为超参，它们具体意义下面详解。
上面给出了通用框架，如何写出具体的似然函数呢？当然需要针对具体问题进行分析，抽象出问题特点来给出。下面，看一个简单处理思路，即假设：
1）目标数据（target data）是由一个光滑的，且具有加性零均值高斯噪声（additive zero-mean Gaussian noise）函数生成。这时，对于给定输入x，得到目标值t的概率为
其中，
控制噪声的方差。
2）数据独立同分布
这时，权重的似然函数为：
5.权重的后验概率
前面，以及了解了权重的先验 ，和似然
，很容易通过贝叶斯准则得到其后验概率
其中，
。
有了这套东西，通过解就可以得到权重的最大后验概率解
。当，先验为高斯，噪声模型为加性零均值高斯时有
到这里，能看到贝叶斯技术如何巧妙的将最大似然技术（误差平方和最小）和正则化（权重衰减）技术结合起来了。当数据集较大，随着训练进行，上式中第1项会随着增大并成为主导，同时第2项重要性逐渐减弱。当数据集较小的时候，第2项（对应于先验）在决定解就会起很重要作用。
6.后验概率的高斯近似
前面得到权重的后验概率
，然后当然希望利用它进一步做如下事情：
1）计算神经网络输出的概率分布
2）计算模型参数的Evidence，以进行模型选择
第0部分，我们了解了贝叶斯技术在进行预测时候是对多个模型进行加权平均进行的，相当于对整个权重空间进行积分。很多情况下，积分是很难进行的，就需要通过近似方法来求解。
MacKay(1992d)利用高斯近似（Gaussian approximation）来计算后验概率，通过对
在极小点出进行泰勒展开，并保留2阶项，而实现的。
这样得到的后验概率是权重的高斯函数
，
注意：这里给出的是单个高斯近似，并未考虑存在多个极值的情况。
