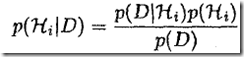虽然该章主要讨论贝叶斯技术(Bayesian Techniques)在Neural Networks中应用,但其内容对与做Machine Learning还是非常有启发的。尤其现在Bayesian Learning,以及Graphical Model在Jordan、Bishop等牛人带领下已经成为Machine Learning主流之一的情况下,通过回归经典文献可以让我了更容易领略其中奥秘。
1.贝叶斯技术的特点
1)提供了一个框架(framework),传统的基于误差最小化(Error Minimization)的学习方法都是贝叶斯方法的近似或特例;正则化(Regularization)可以更加自然的给出解释
2)对于回归问题,给出预测值的同时,也可以给出置信区间
3)仅利用训练数据就可以做很多有意义的事情(传统方法需还需要测试数据)
a)选择合适的正则化系数;
b)模型选择。它提供了客观的框架来处理模型复杂度,同时避免了使用最大似然(Maximum Likelihood)方法中的问题
4)可用于判断是否需要在输入空间(Input Space)中增加新数据,以使之蕴含更多信息(MacKay,1992c)
5)可用于特征选择:基于Automatic Relevance Determination (MacKay, 1994a,1995b; Neal, 1994)方法。
2.贝叶斯技术的初探
下面通过了解常用的误差最小化方法训练模型时存在的问题,及贝叶斯方法是如何优美解决的来初步了解它的思想。
当采用误差最小化方法训练模型时,一般来说,模型越复杂对训练数据拟合越好,但这不能保证它的推广能力也好。这时,只能用交叉验证来处理。而贝叶斯方法采用完全不同机制处理模型复杂度问题,并且它运行将全部数据作为训练数据。
为清楚解释,咱们看一个假定的例子:
1)有三个模型H1,H2,H3,它们复杂度依次增加。
a)每个模型都有固定的结构(隐层个数、每层节点数、激励函数等),以及可调节的参数(如权重)。
b)调整参数值,每个模型都可以表达一定范围的输入-输出映射函数。模型越复杂,它所能表达的函数范围越广。
那么,当有此数据集D后,模型的后验概论为
1)P(Hi)为模型先验(其实就是哪个模型更好的概论表达)。一般很难倾向于某个模型时,就给所以模型赋予同样的先验概率。
2)P(D)为归一化因子(概率值域为[0,1])。它与模型无关。
3)P(D|Hi)为模型Hi的Evidence。判断模型复杂度是否合适(即模型选择),可通过比较Evidence来抉择。
各模型的Evidence绘图,可看出如下门道:
1)模型越复杂,它能描述数据集越广(即能表达更大范围的函数)
2)对某一具体数据集D0 来说,模型H2的Evidence最大。这说明Evidence偏爱复杂度适中的模型。
到此,大家会有一个认识,即在贝叶斯方法中,一般选Evidence最大的模型。其实,并没有这么简单。正确的贝叶斯方法会利用所有的模型,它会将所有模型的输出进行加权而得到最终输出,其权重就是每个模型的Evidence。越好的模型对输出贡献越大。同时,因为Evidence是通过训练数据获得的,因此可以无需单独切分出测试数据,也就无需交叉验证了。
通过前面例子,我们可以体会到贝叶斯方法的一个重要概念-Marginalization,对不想要或不关心的变量通过积分消掉。