Lecture 3 -- Why Deep Structure is good?
1. 还记得之前所说的分段线性函数拟合方式吗？
我们可以将任意的曲线视为分段线性函数，只要我们在曲线上采样的点足够多，就可以做到无限逼近;
一个Neuron可以表示一种“阶梯型”曲线，因此，理论上，只要我们有足够多的Neuron，我们只需要一个Layer，我们就可以拟合任意的Function！
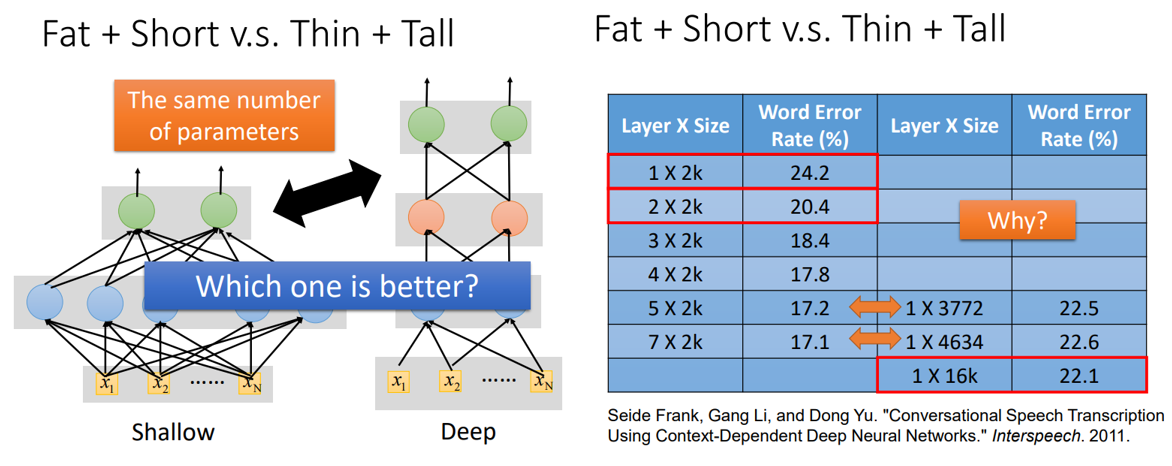
既然一个Hidden Layer就能拟合任意的Function，那么为什么我们还需要Deep的Neural Network，而不是Fat的Neural Network呢？
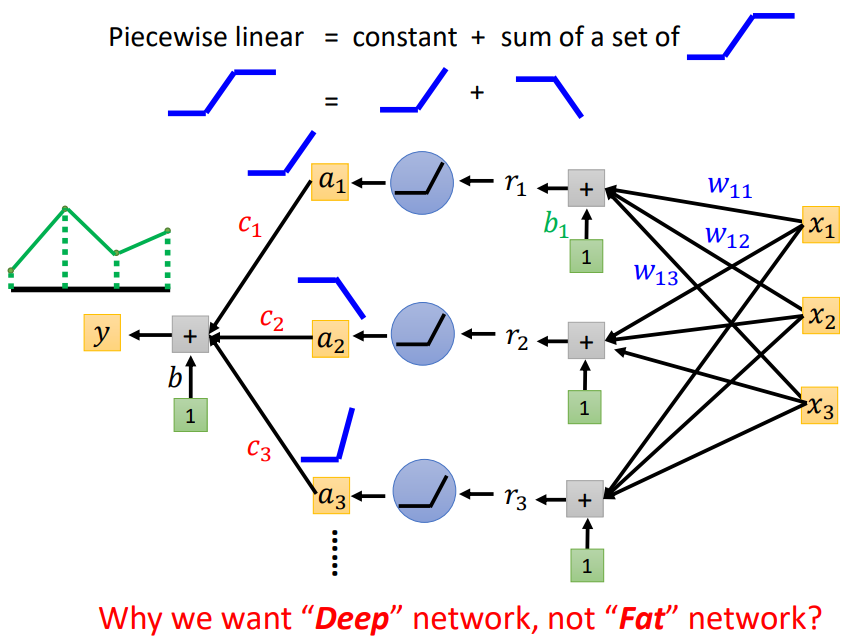
2. Why we need deep?
Frank等人的实验表明，同样的/近似的参数量，更深的网络表现更好！
我们来看一看网络加深的过程中发生了什么？（举一个简单的例子）
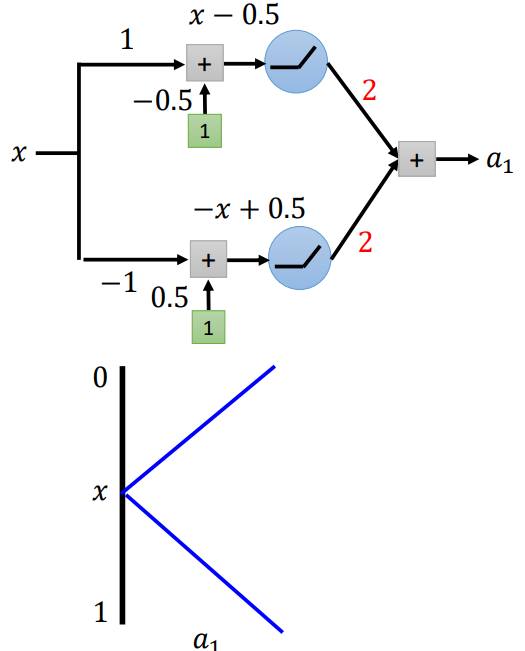
先以一层为例，激活函数使用ReLU，x从0-1变化时，a1从1-0-1
接着，我们再以同样的方式增加一层：
同理：a1和a2的关系与x和a1的关系相同；
那么，x和a2的关系是怎么样的？
当x从0-0.5时，a1从1-0，此时a2从1-0-1；
当x从0.5-1时，a1从0-1，此时a2从1-0-1；
因此，x和a2的关系如上图所示。（两层网络有22条折线）
同样地，我们继续增加网络深度：
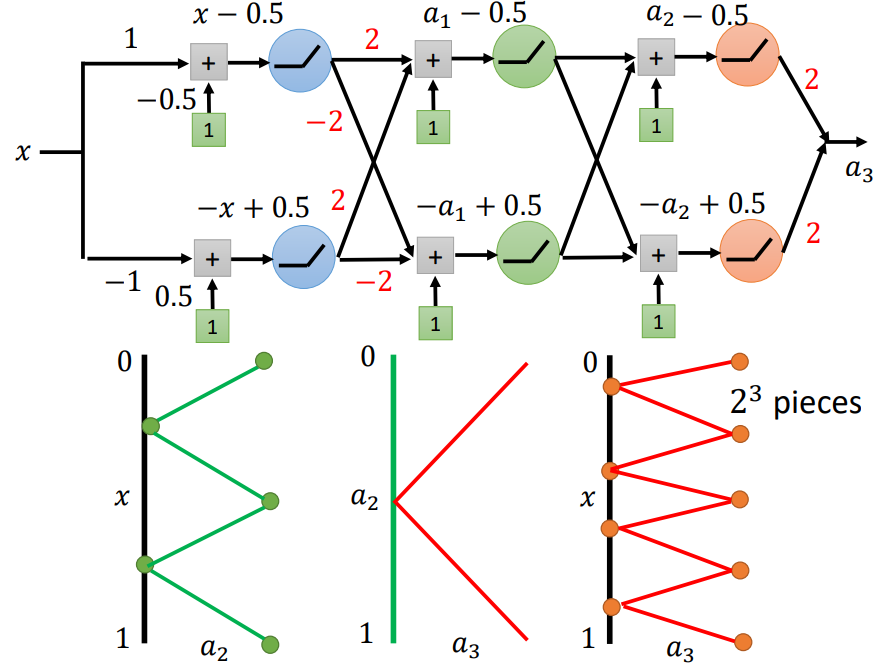
三层网络有23条折线
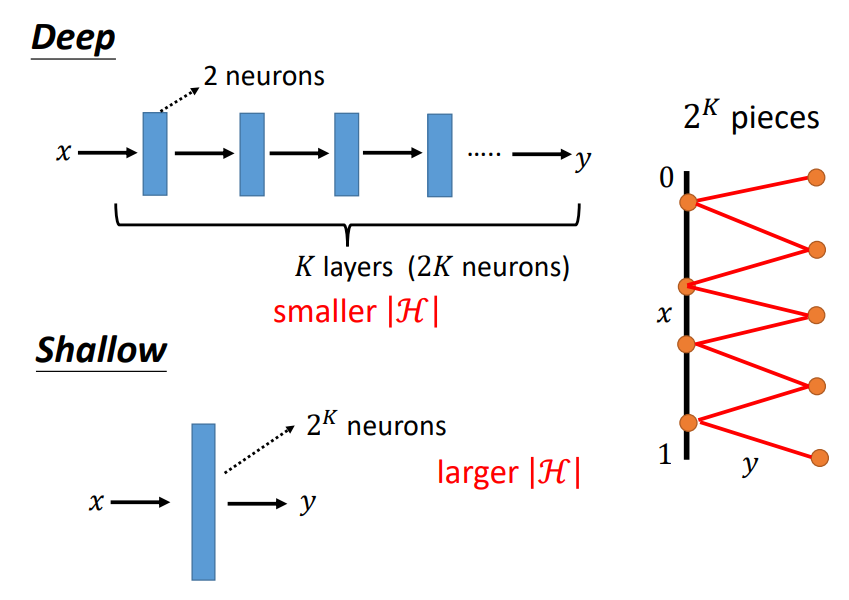
K层网络有2K条折线！
根据之前所学习的内容，我们知道：
像这样有2K条折线的分段线性函数，我们至少需要2K个“阶梯型”曲线，
也就是说，如果我们只用一个Hidden Layer，那么这个Hidden Layer至少要有2K个Neuron！也就是说网络中有2K个参数(不考虑bias)；
而如果我们使用Deep的Neural Network，我们需要2K个Neuron！也就是说网络中有2*2*(K-1)+2+2=4K个参数(不考虑bias)；
在实际的任务中，我们需要拟合的Function往往是非常复杂的，如果我们只使用一个Hidden Layer，那么模型的参数量会指数级上升；
也就是说模型的弹性很大，非常容易过拟合，此外，Function set也变大，为了使“理想”和“现实”更加接近，我们需要非常大的训练资料！
因此，这似乎与我们的认知相反，我们往往会认为更加Deep的网络架构，会需要更多的训练资料，实则不然！！！
Fat且Short的网络架构反而需要更大笔的训练资料才能表现更好！！！
因此，Deep Learning是一个鱼和熊掌可以兼得的方法！！！
相较于Shallow的Network，它能使网络中的参数减少的情况下依然保持较低的Loss！！！
END
