Lecture 2 -- Local Minima & Saddle Point
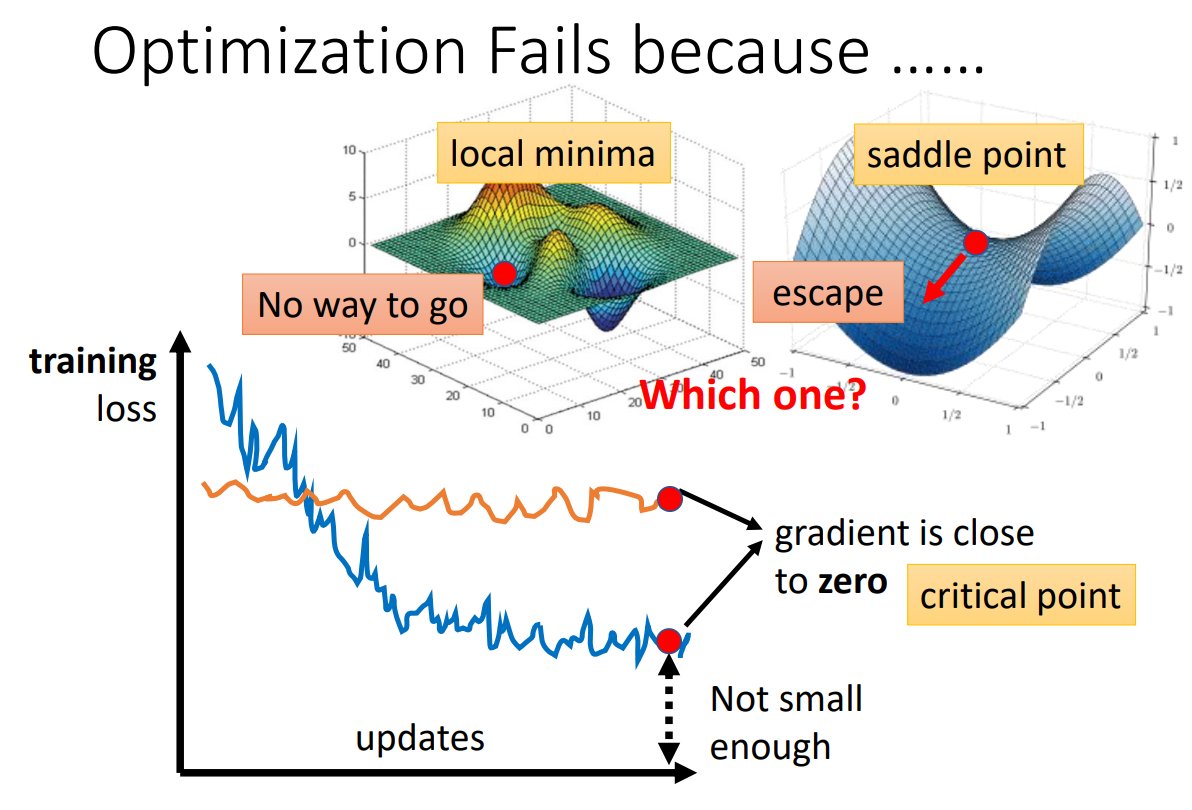
1. Optimization Fails because ...
-
local minima(局部最小值)和saddle point(鞍点)都会造成梯度为0，导致参数无法继续更新下去，损失趋于平缓
-
local minima和saddle point统称为critical point(驻点)
2. 如何判断一个点是saddle point还是local minima？
θ'附近，损失函数L(θ)可近似表示为L(θ) ≈ L(θ') + (θ-θ')Tg + 1/2(θ-θ')TH(θ-θ');
如果θ'是critical point, 则g=0, L(θ) ≈ L(θ') + 1/2(θ-θ')TH(θ-θ');
1/2(θ-θ')TH(θ-θ')的正负决定了critical point, 即θ'的类型
⭐具体判断方式：
当Hessian matrix的所有eigen values(特征值)均为正数，则θ'为Local minima
当Hessian matrix的所有eigen values(特征值)均为负数，则θ'为Local maxima
当Hessian matrix的eigen values(特征值)有正数，也有负数，则θ'为Saddle point
什么是Hessian Matrix？
3. Don't afraid of saddle point!
如果此时θ'为saddle point，那么，H的特征值有正数，也有负数；
我们假设λ(λ＜0)是H的其中一个特征值，与λ对应的一个特征向量为μ；
令θ-θ'=μ，则(θ-θ')TH(θ-θ')=μTHμ=μT(λμ)=λ||μ||2<0；
也就是说，此时L(θ)<L(θ')；
因此，当θ-θ'=μ，即θ更新为θ'+μ时，会使损失降低！
综上所述：当遇到鞍点(saddle point)时，只要将参数θ加上H矩阵特征值小于0对应的一个特征向量，即可跳出鞍点，沿着损失降低的方向继续更新参数！
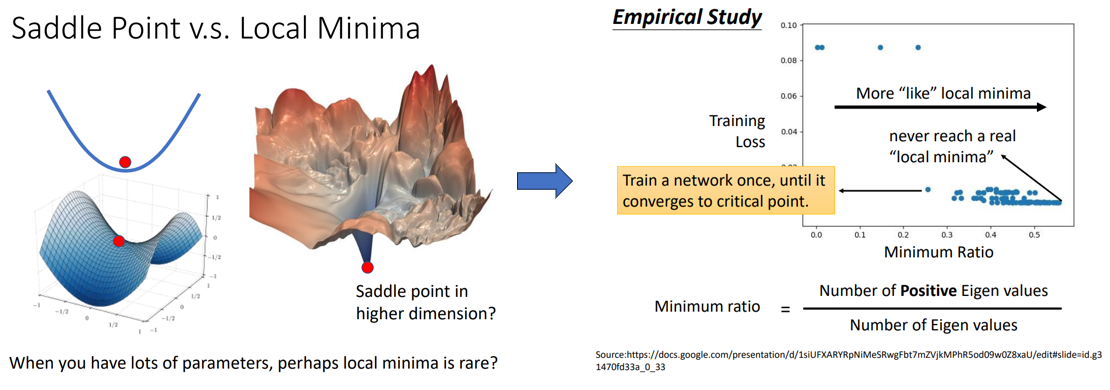
实际上，我们并不需要太担心局部最小值的问题，因为当你的模型有很多参数时(损失函数处在高维空间)，或许局部最小值会很稀少！
也有人做过实证研究(Empirical Study)，如下图，每一个蓝色的点代表一个模型，每个模型训练到critical point处停止，
计算此时H矩阵的特征值发现，没有一个critical point处的H的特征值全为正数，即没有local minima的情况，这从侧面反映了或许高维空间中saddle point为主要的critical point，local minima很少出现！
END
