Lecture 1 -- Discriminative Model & Generative Model

1. Probabilistic Generative Model

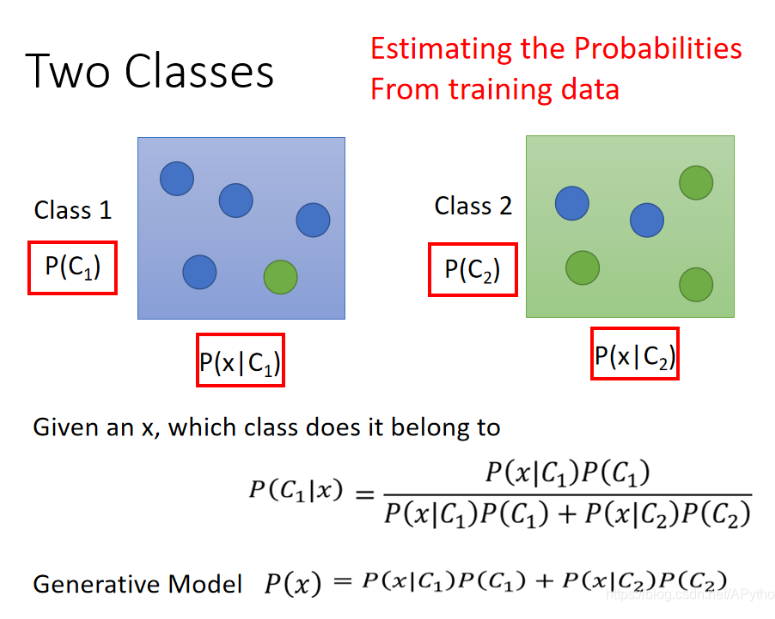
  • 概率生成模型，关键是求上图红框内的四个概率值！
  • 我们假设Class 1有N1个样本，Class2有N2个样本，则P(C1)=N1/(N1＋N2)，P(C2)=N2/(N1＋N2)
  • 如何求P(x|C1)和P(x|C2)?

 

 

2. 如何求P(x|C1)和P(x|C2)?

我们假设Class 1的所有样本是从一个Gaussian Distribution中采样而来；Class 2中所有的样本也是从一个Gaussian Distribution中采样而来。

 Gaussian Distribution：

高斯分布会随着μ和Σ的变化而变化，我们的目标就是找到最有可能产生Class 1这些样本的高斯分布的μ1和Σ1值以及最有可能产生Class 2这些样本的高斯分布的μ2和Σ2值

怎么找？ → Maximum Likelihood

  • 最佳的μ和Σ是有公式可以直接确定的，当然也可以通过计算L对μ和Σ的偏微分得到结果
  • 当我们找到最有可能产生这两类数据的高斯分布后，我们便可计算P(x|C1)和P(x|C2)，计算后验概率，得到最终预测结果

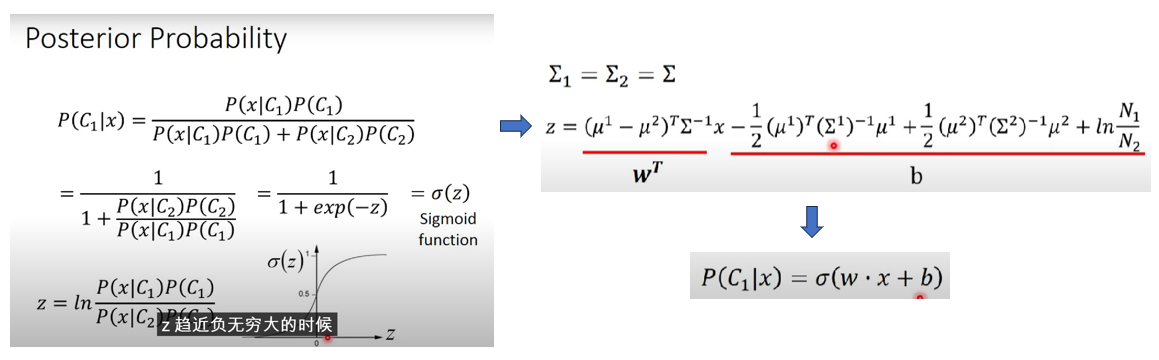
实际上，两个类别的高斯分布的Σ通常是共用的，如上图所示。μ1和μ2不变，Σ是两个类别Σ1和Σ2的加权平均值！

 

 

3. 从另一个角度看Probabilistic Generative Model,它其实和逻辑回归的Model(Function Set)完全一致！

从上图中很容易看出，当不同类别的协方差共用时，概率生成模型的Model和逻辑回归完全一致，只是概率生成模型的w和b是间接得到的，需要计算μ1、μ2和Σ，而逻辑回归的w和b是直接通过梯度下降得到的 (中间的具体计算过程省略，可自行推导)，像逻辑回归这种直接得到w和b的模型称为Discriminative Model，而需要计算先验概率和条件概率而得到后验概率的模型称为Generative Model，如下图所示

 

 

4. Discriminative v.s. Generative

Generative模型的一些优势如上

 

 

5. 逻辑回归交叉熵损失的推导

同样也是让所有训练样本出现的机率最大！！！

有趣的是，当逻辑回归使用交叉熵损失函数时，其参数的Update的公式和线性回归完全一致！！！

Logistic Regression v.s. Linear Regression

 

 

 

6. 为什么逻辑回归不用MSELoss()作为损失函数呢？

  • 当预测值和真实值很接近或者很远时，其微分值都为0！

  • 当距离目标值很远时，微分值接近0，参数更新速度很慢！

  • 参数更新速度慢，将学习率调大也不行，因为此时也可能距离目标很近

 

 

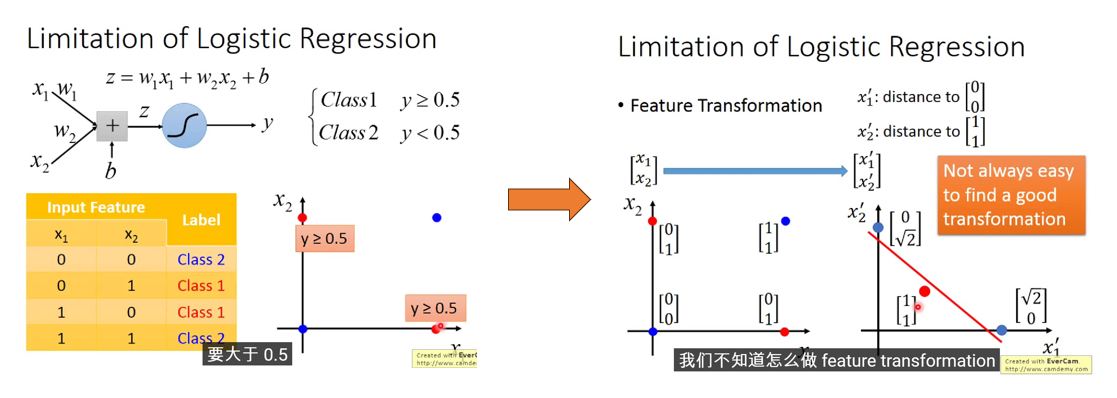
7. 逻辑回归的限制

  • 由于逻辑回归的Boundary是一条直线，因此无法分类Class 1: [0, 1], [1, 0]和Class 2: [0, 0], [1, 1], 通常的做法是进行Feature Transformation，但这种转换通常不容易人工做到
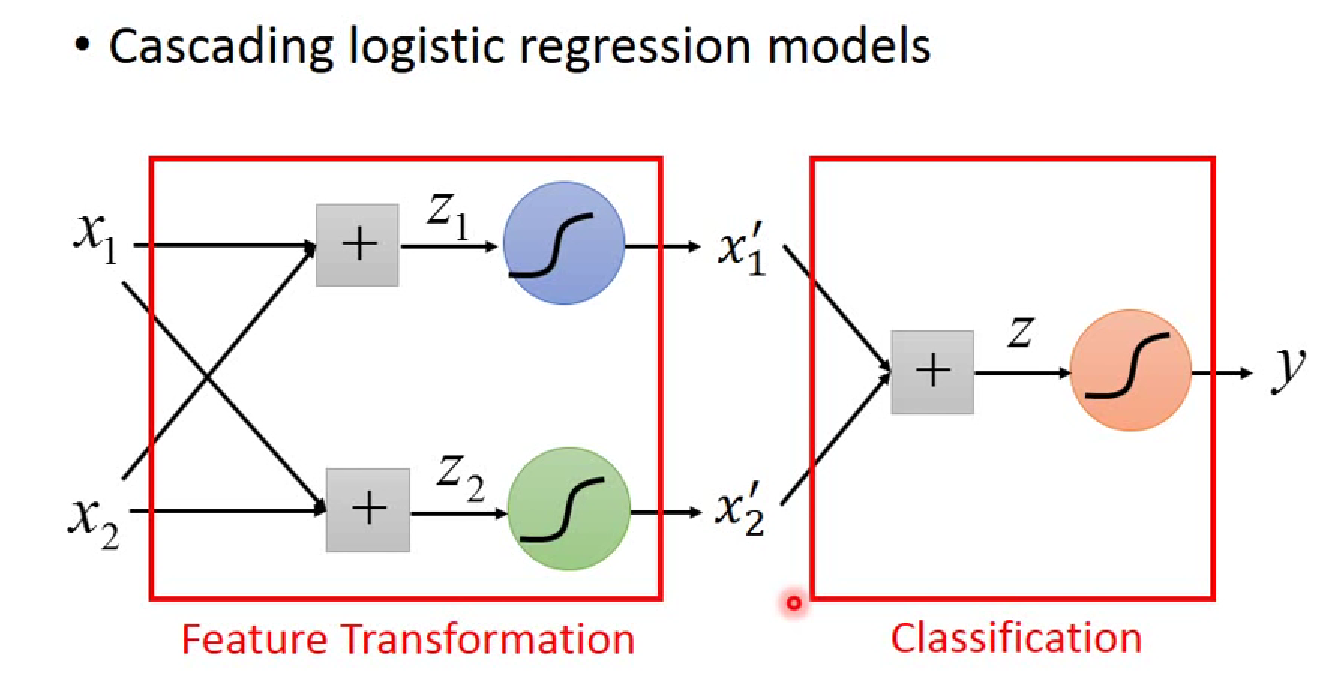
  • 将多个逻辑回归进行堆叠可以做到这一点  ------  Neural Network！

 

 

END
posted @ 2023-07-19 01:29  Peg_Wu  阅读(15)  评论(0)  编辑  收藏  举报