Lecture 1 -- Preparation
1. 机器学习的任务
Machine Learning ≈ Looking for Function (⭐)
- Regression: The function outputs a scalar
- Classification: Given options (classes), the function outputs the correct one
- Structured Learning: Creat something with structured (image, document) -- “让机器学会创造”
2. 机器学习的步骤
Step 1: Define a Function with Unknown Parameters (Model) -- Based on domain knowledge
Step 2: Define Loss from Training Data
-
Loss is function of parameters -- L(w, b)
- Loss: how good a set of values (w, b) is
Step 3: Optimization w, b
-
$w^*,b^*=\underset{w,b}{argmin}L$
-
Gradient Desent (⭐)
- (Randomly) Pick an initial values $w^0,b^0$
- Compute:
$$\displaystyle\frac{\partial L}{\partial w}|{w=w^0, b=b^0}$$
$$\displaystyle\frac{\partial L}{\partial b}|{w=w^0, b=b^0}$$
$$w^1\gets w^0-\eta \displaystyle\frac{\partial L}{\partial w}|{w=w^0, b=b^0}$$
$$b^1\gets b^0-\eta \displaystyle\frac{\partial L}{\partial b}|{w=w^0, b=b^0}$$
-
- Update w and b interatively
总结：搭建模型 --> 前向传播 --> 计算损失 --> 反向传播 --> 更新参数
3. Linear Model → Neural Network
3.1 Linear Model
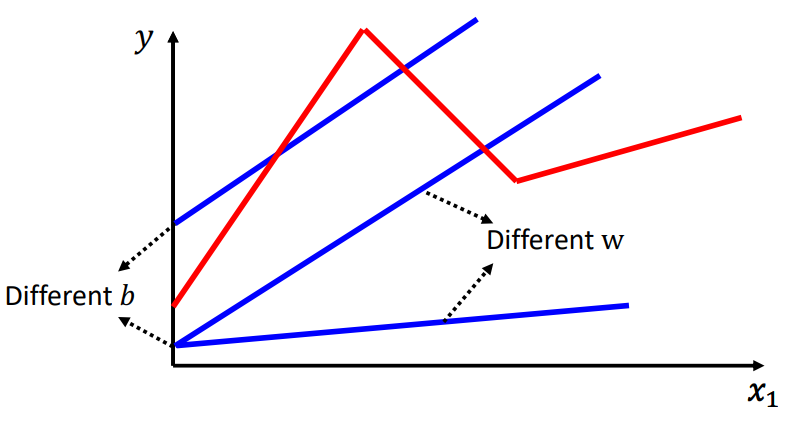
Linear models are too simple！图中的红色曲线(Piecewise Linear Curve)显然无法用线性模型拟合！线性模型很明显存在Model Bias！这种情况我们应该怎么办？
3.2 How to fit Piecewise Linear Curves?
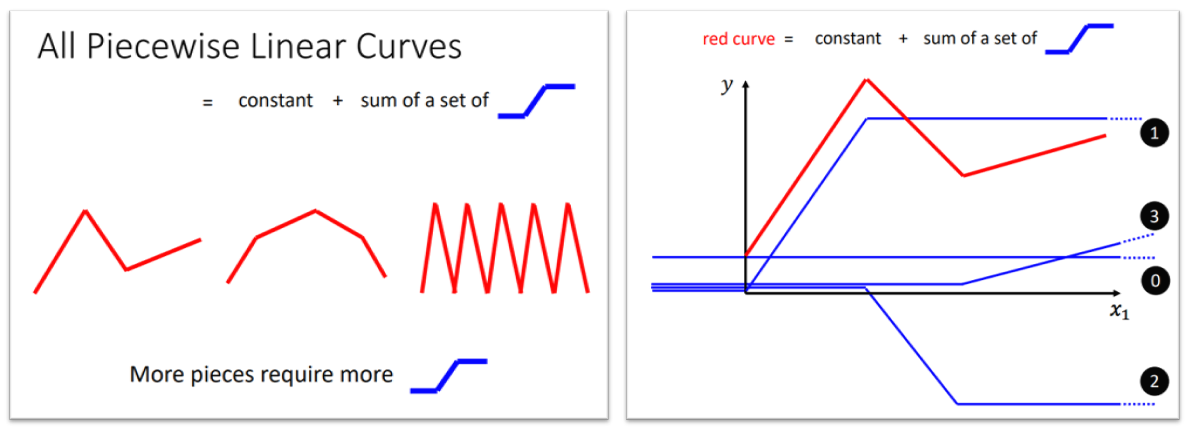
- 任何一个分段线性函数，都可以表示为: 常数 + n个“__/一”(⭐)
- 如上图(右)，红色曲线 = 曲线0 + 曲线1 + 曲线2 + 曲线3
- 扩展到曲线，我们只需要在曲线上找到足够多的点，即可把任意一条曲线看作分段线性函数，同样可以对其进行拟合！
3.3 How to represent function “__/一”?
通常使用Sigmoid函数，如下图所示。
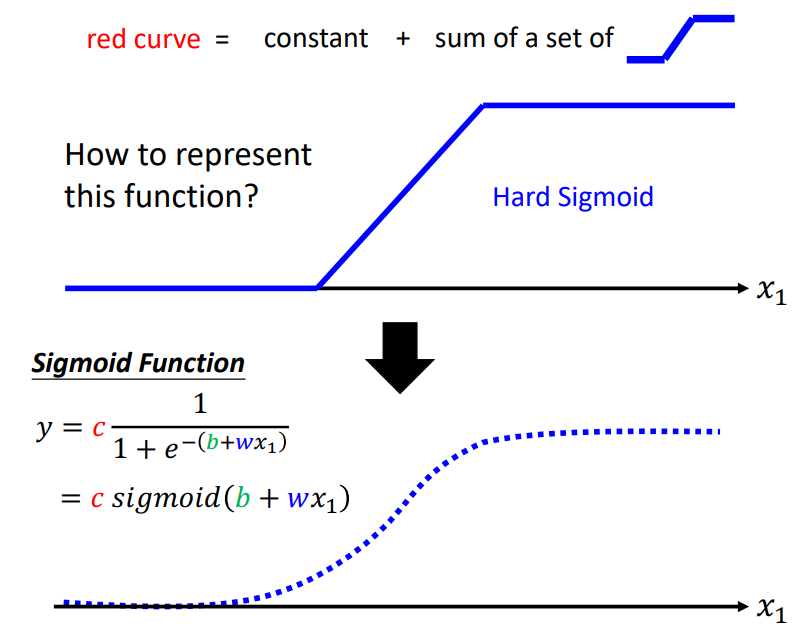
- 因此，3.2中的Red Curve: $y=b+\displaystyle\sum_i{c_isigmoid\left( w_{\text{i}}\text{x}+\text{b}_{\text{i}} \right)}$
- 推广到j个特征，$y=b+\displaystyle\sum_i{c_isigmoid\left( \displaystyle\sum_{\text{j}}{\text{w}_{\text{ij}}\text{x}_{\text{j}}}+\text{b}_{\text{i}} \right)}$
4. Issues
- Gradient Descent中，面临的最大的问题其实不是Local Minima？
-
ReLU和Sigmoid哪个激活函数更好，为什么？
-
为什么我们想要更“Deep”的Network，而不是更“Fat”的Network？
-
我们该如何进行模型的选择？
END
