动态规划题目总结
本篇总结涉及的题目包括两道经典的动规题目(来自头条题库)及剑指offer中的所有(10道)动归题目(题目分类链接见文末)。
动规问题是算法中比较经典并且比较难的一类算法,通常解决该类问题的思路是:
① 假设状态(从问题中抽象出dp[i]或者dp[i][j]的含义)
② 找出状态转移方程(待求解问题和子问题的关系)
③ 确定边界(一般问题都有初始值,或者需要考虑特殊情况)
④ 确定实现方式(自上而下或者自下而上,本篇博客都采取的是自下而上的实现方式,因为该方法更加高效)
经典题1:编辑距离
题目描述:给定两个字符串,允许增加,删除或者修改字符来使得两个字符串一致的最少操作次数。
假设状态:dp[i,j]代表字符串s1的前i个字符和字符串s2的前j的字符的编辑距离
状态转移方程及边界:

代码实现:
理解并写出状态转移之后,代码实现就比较容易了,考察代码能力。首先可以先画出这个二维表,长和宽分别为两个字符串的长度m和n。由于dp[i,j]依赖于dp[i-1,j-1], dp[i-1,j]和dp[i,j-1],也就是一个元素依赖于其左边上边和左上角的三个元素,因此只需填充初始值,接着按行计算就可以了,填完表后,我们要返回的值就是dp[-1][-1],也就是最右下角的值。后续代码实现类似,不详细展开,具体代码实现见文末。
经典题2:最长回文子串
题目描述:一个字符串中最长的具有回文特征的子串。(子串是连续的,子序列是可以不连续的)
假设状态:dp[i,j]代表dp[i]到dp[j]是否为回文串
状态转移方程及边界:
dp[i,j]=dp[i+1,j-1] and (dp[i]==dp[j])
实现注意:对角线为T,左下三角为F。因为依赖左下角元素,所以需要计算出连续2个字符的回文情况才可以用状态转移计算其他的。
下面前4道都是和Fibonacci数列相关的题目,2-4主要是问题抽象和思路转化。
剑指1:Fibonacci数列
题目描述:0,1,1,2,3,5,8,...
假设状态:dp[i]代表第i个元素的值
状态转移方程及边界:子问题非常明显,可以直接根据题意写出

剑指2:矩形覆盖
题目描述:n个2x1的矩形去覆盖2xn的矩形,有多少种覆盖方法

假设状态:dp[i]代表当n为i的时候的方法数,因为每次可以竖着放一个或者横着放两个,所以有两种选择,只需考虑剩下的部分即可。当然另外一种方法是你写出前几个的方法数,找规律,但是如果没有特别明显的规律就不可行了。
状态转移方程及边界:
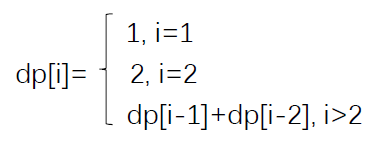
剑指3:青蛙跳台阶
题目描述:n个台阶,每次跳1或2个,求跳法数。
假设状态:dp[i]代表当n为i的时候的方法数
状态转移方程及边界:
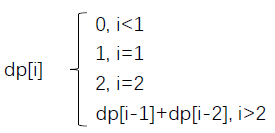
剑指4:变态跳台阶
题目描述:n个台阶,每次跳1/2/.../n个,求跳法数。
假设状态:dp[i]代表当n为i的时候的方法数
状态转移方程及边界:
dp[1]=1, dp[2]=2
dp[i]=dp[i-1]+dp[i-2]+...+dp[0]
dp[i-1]=dp[i-2]+...+dp[0]
所以dp[i]=2dp[i-1]=2i-1
剑指5:连续子数组的最大和
题目描述:一个数组中连续子数组和的最大值
假设状态:这里比较难,要找到子结构。因为子数组的起始和末尾都可以不固定,这样子结构就是任意的。我们可以固定起始位置,实现如下图所示的子结构。
![]()
dp[i]代表以nums[i]为结尾的连续子数组的和的最大值,最后再取dp数组中的最大值即所求。
状态转移方程及边界:

dp[0]=nums[0]
剑指6:礼物的最大价值
题目描述:一个数字矩阵,从左上角走到右下角路径和的最大值,只能向右或向下走。
假设状态:dp[i,j]代表走到(i,j)时候获取的最大值。
状态转移方程及边界:
dp[i,j]=max(dp[i-1,j], dp[i,j-1])+Arr[i,j]
剑指7:最长不含重复字符的子字符串
假设状态:和上上道题目类似,dp[j]代表以str[j]结尾的不重复子串的最大长度。
状态转移方程及边界:
假设str[j]左边最近的满足str[i]=str[j]的字符str[i]:
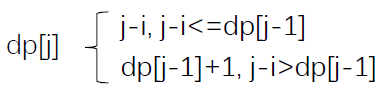
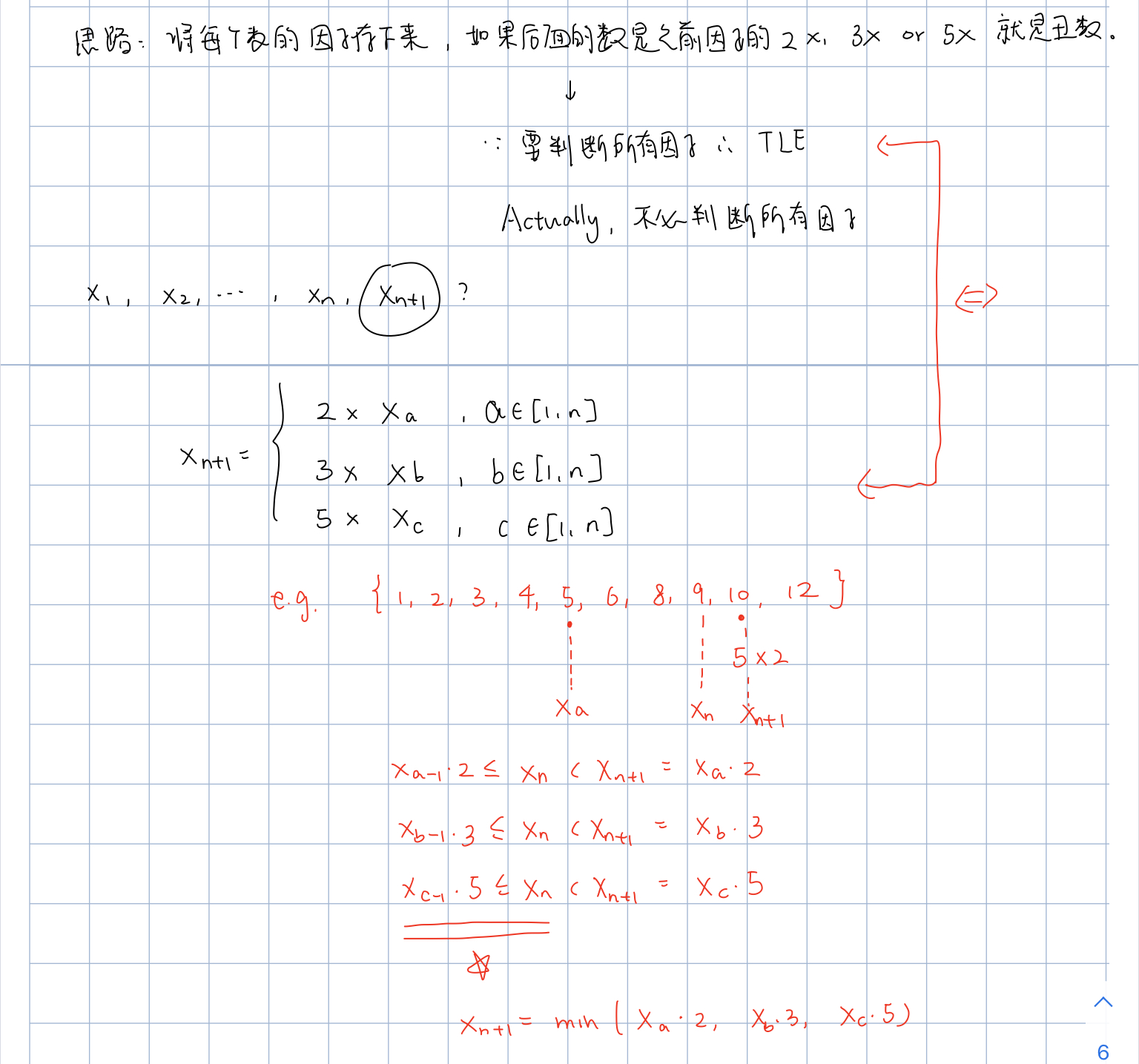
剑指8:丑数
题目描述:只含因子2,3,5的数叫丑数,求第n个丑数。
假设状态:dp[i]
状态转移方程及边界:
本题目需要一些数学推导来简化过程,否则也会超时
剑指9:n个骰子的点数
题目描述:掷n个骰子,向上面之和的所有概率
假设状态:这个题首先可以化简为向上面之和出现的次数,因为最后只要除以6n即可。然后将少掷一个骰子剩下的骰子看作子问题。dp[i,j]代表投完i个骰子后,点数和为j的情况数。
状态转移方程及边界:
对于最后一个骰子,其值取1到6,然后考虑子问题,如果最后一个骰子为1(已经确定),那么总情况数为dp[i-1,j-1],所以考虑6种情况:
dp[i,j]=dp[i-1,j-1]+dp[i-1,j-2]+dp[i-1,j-3]+dp[i-1,j-4]+dp[i-1,j-5]+dp[i-1,j-6]
(这个状态假设还是比较难的,所以最开始用自己的方法实现,然而超时了,详见代码)
剑指10:构建乘积数组
题目描述:求一个数组对应的乘积数组,其中一个数对应的乘积是原数组中除了该数之外其他数的积。
实现思路如下:
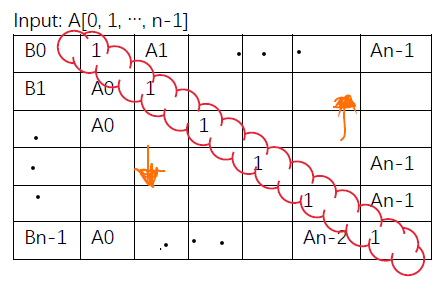
子问题就是不同长度的连续乘积,最后将两侧乘起来返回即可。
Ref:
自己的题解(可能偶尔有的题参考了别人的code,侵删):https://github.com/Cinderella0709/LeetcodePy/blob/main/DynamicProgramming.py


