数字图像基本处理——空间滤波(spatial filtering)
空间滤波器主要包括平滑滤波器和锐化滤波器,下面从理论和实践两个部分阐述。
理论
空间滤波的公式如下:
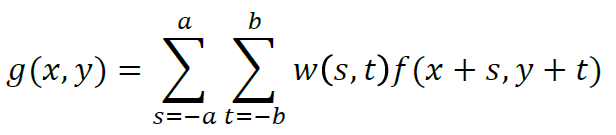

空间滤波的过程也就是不断用一个filter(一般为3X3)在图像上与同样大小的局部patch作用,作用结果更新在中心点上,所以需要m,n为奇数。
在2维时域信号上做卷积与此公式稍有不同,如下:
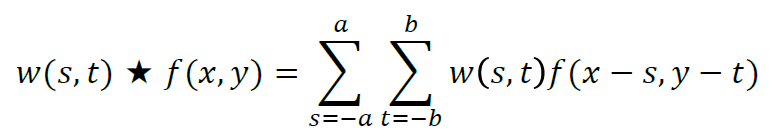
可以看到,空间滤波公式中两个+变成了-,对应于空间滤波中的filter旋转180度之后的filter相作用,所以当filter为对角线对称的时候,空间滤波与2维卷积是一样的,而通常filter是对角线对称的。区别于卷积,一般将空间滤波描述为correlation,即看filter和图片上local patch的相关性。
1、平滑滤波器
平滑滤波器的两个主要作用是模糊化和降噪(如美颜相机中的磨皮操作)
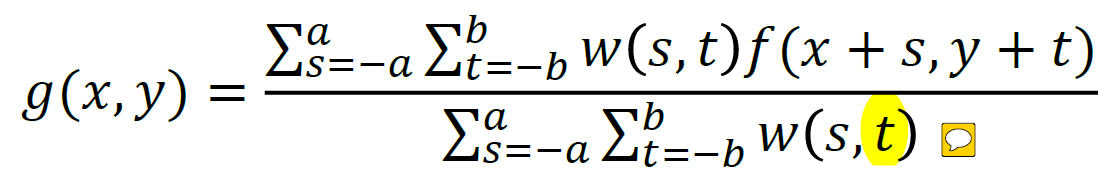
分母除以一个数保证变换后强度不会大增。
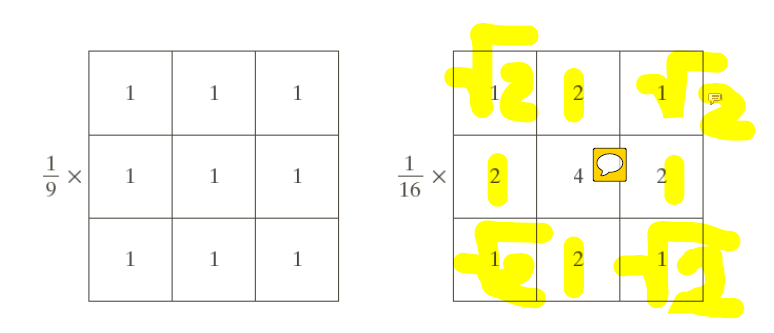
1.1 线性滤波
常用的线性滤波有均值滤波(频域上的低通滤波器)和高斯滤波。下图分别是均值滤波器(左)和高斯滤波器(右)示例:
一个例子就是处理如下左图,只想保留较大的点,通过平滑过滤器模糊化,将小点融合,该地方有个trick就是因为该图对比度比较明显,可以通过加阈值来截断亮点和暗点。
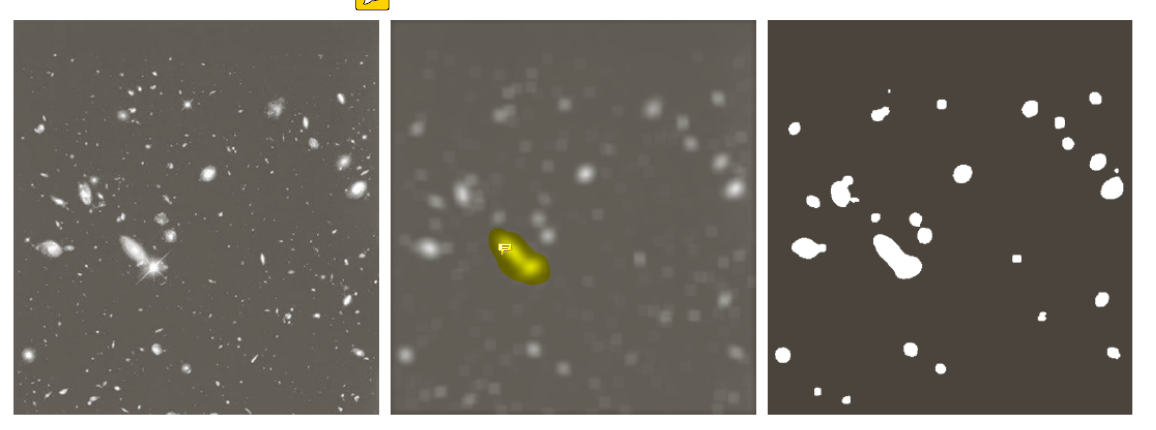
1.2 非线性滤波
常用的线性滤波有中值滤波和最大值滤波。
中值滤波器:
![]()
从上式很容易看出中值滤波就是在输入图像的patch上用中值代替该点。中值滤波器适用于突变的噪声点,尤其是impluse noise和pepper noise。
2、锐化
锐化就是突出边缘信息,而边缘会有像素点上的突变,所以可以用导数来检测边缘。
一维空间中一阶导数和二阶导数如下:(一阶导数就是导数的定义,二阶导数利用一阶导数的公式求解得,需要替换一次自变量)
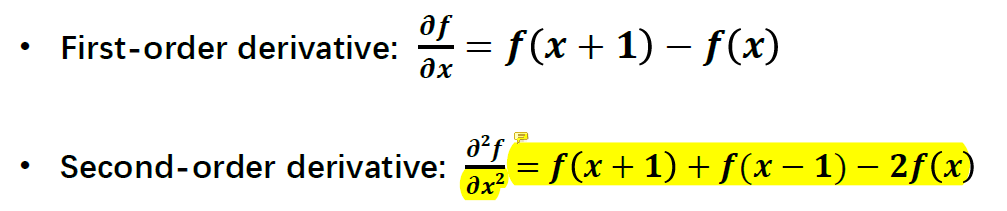
二维空间中,需要对x,y求偏导
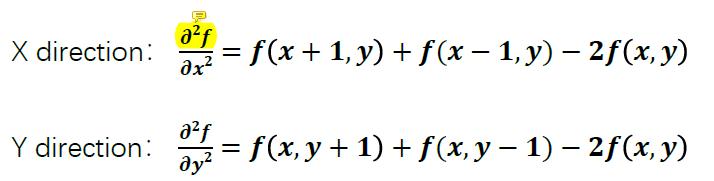
求和得到2维空间中的2阶导数(这也就是拉普拉斯算子):

上式也可以写成一个3X3的spatial filter(系数对应filter中的值):
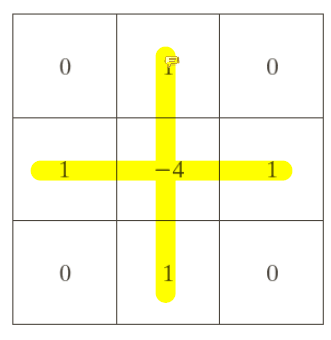
这个滤波器叫做Laplacian Filter Masks,类似的还有:
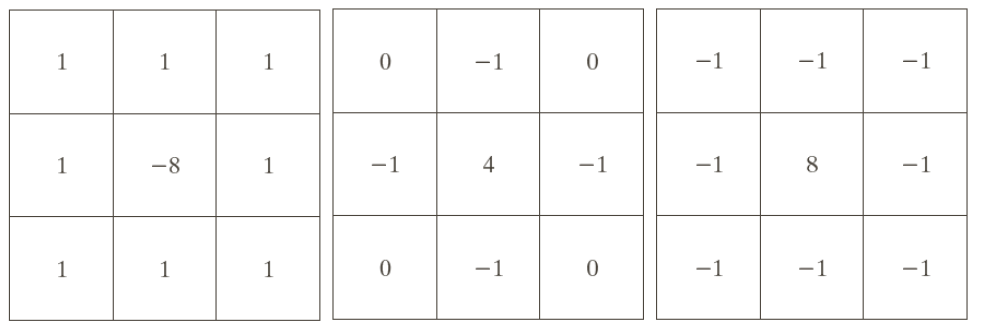
由于Laplacian Filter Masks对应的是二阶导数,可以检测出边缘信息,但是导数相较于原图,损失了强度,所以锐化需要叠加上原图的信息,只需再加上一个只有中间值为1的filter,也即在Laplacian Filter Masks中间的值上+1(如4+1)/-1(如-8-1)。
实践
下图是一个overall的结果,后续的结果都基于此进行调整:
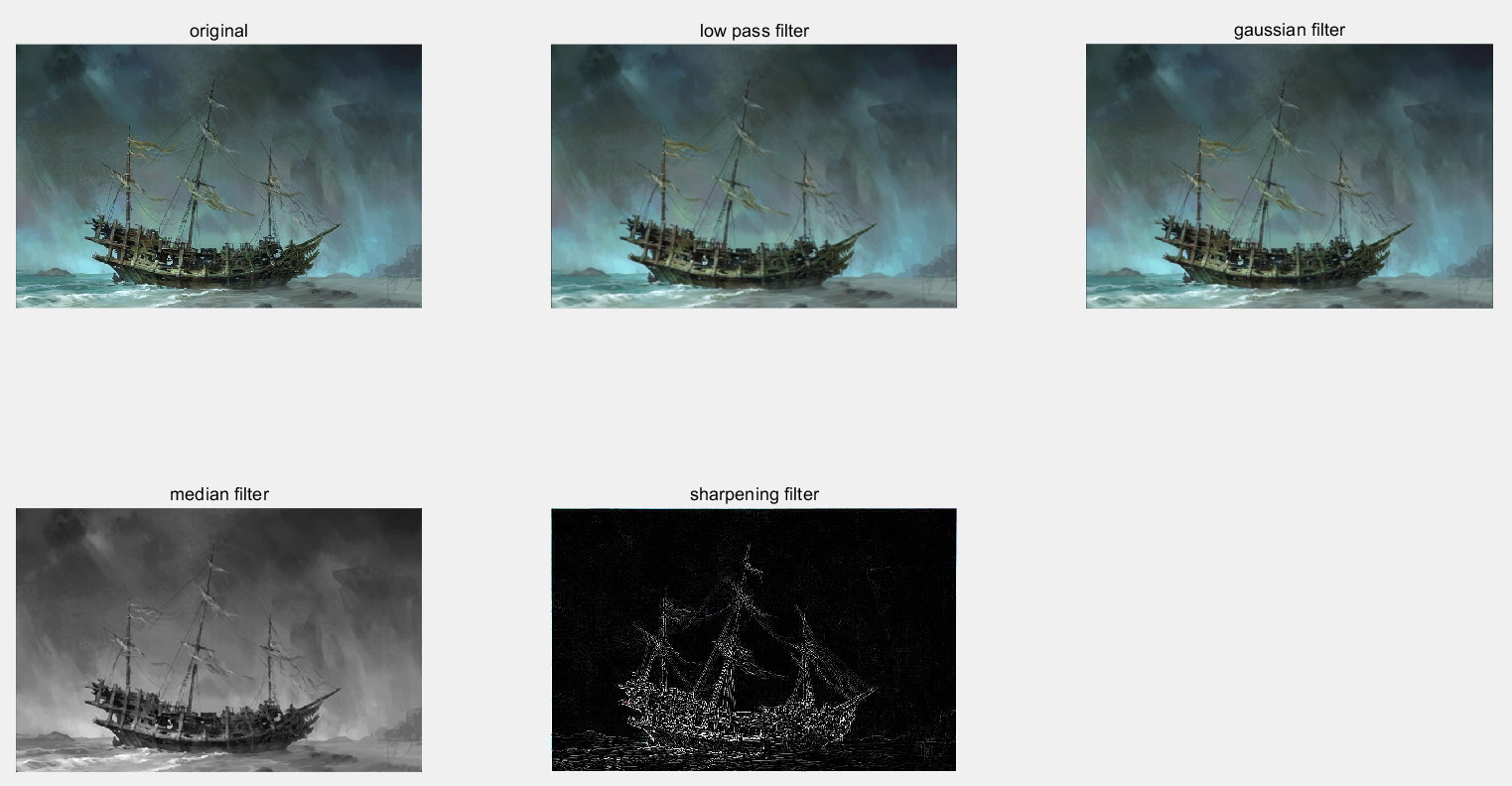
可以看出平滑后的船体要稍微模糊一些。基于此,我们可以增加low pass filter的尺寸来观察结果,我们将原来的3X3,改为5X5,结果如下:
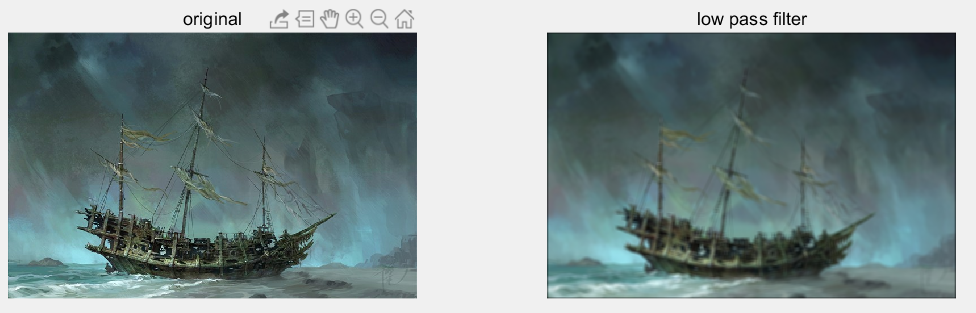
可以看出,增大低通filter size,图像更加模糊。
我们可以看出第一张图的subplot5只得到了图像的边缘,为了恢复图像的原本信息,需要叠加上原始图像信息,更改后结果如下:

为了更清楚的看到中值滤波的效果,更换测试图片:

我们可以看出中值滤波器对于椒盐噪声效果非常好。下面测试一下不同的filter size对中值滤波器结果的影响:
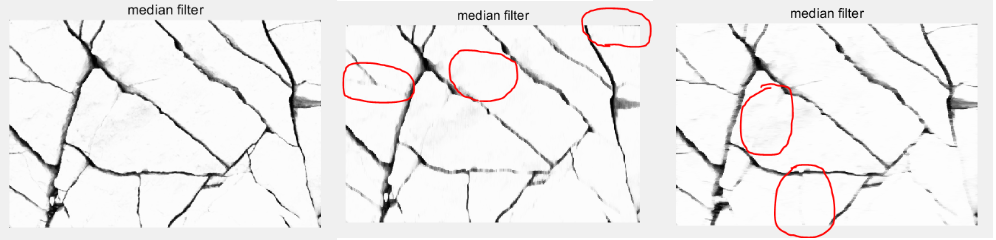
filter size从左到右分别为:[3 3]; [11 1]; [1 11]。我们可以看出后面两种情况可以分别消除横纹或纵纹。
本实践部分代码如下:
addpath('E:\Digital_img_processing\Lecture_5_discussion_spatial_filter');
fig0=imread('ex_median.jpg');
% smooth filter
LP=1/9*[1 1 1; 1 1 1; 1 1 1];
LP1=1/49*[1 1 1 1 1 1 1; 1 1 1 1 1 1 1; 1 1 1 1 1 1 1; 1 1 1 1 1 1 1; 1 1 1 1 1 1 1; 1 1 1 1 1 1 1; 1 1 1 1 1 1 1];
GP=1/16*[1 2 1; 2 4 2; 1 2 1];
if length(size(fig0))==3 % 如果为彩色的,需要转为灰色的,否则不变,由中值滤波使用;也可以调用3D函数,这样就不需要转换
fig0_gray=rgb2gray(fig0);
else
fig0_gray=fig0;
end
fig1=imfilter(fig0,LP);
fig2=imfilter(fig0,GP);
% median filter
fig3=medfilt2(fig0_gray,[3 3]);
% fig4=medfilt2(fig0_gray,[6 6]); 奇数
fig5=medfilt2(fig0_gray,[11 1]);
fig6=medfilt2(fig0_gray,[1 11]);
% sharpening filter 值可能为负,所以需要转成double
SF=[-1 -1 -1; -1 8 -1; -1 -1 -1];
SF1=[-1 -1 -1; -1 9 -1; -1 -1 -1]; % Add the original intensity
fig7=imfilter(im2double(fig0),SF1);
% plot
figure;
subplot(2,3,1);imshow(fig0,[]);title('original')
subplot(2,3,2);imshow(fig1,[]);title('low pass filter')
subplot(2,3,3);imshow(fig2,[]);title('gaussian filter')
subplot(2,3,4);imshow(fig5,[]);title('median filter')
subplot(2,3,5);imshow(im2uint8(fig7));title('sharpening filter')

