有关直线对称的套路与一些题目
利用直线对称解决问题的最经典例子便是卡特兰数,这里不再多说。顺便安利一位大佬的博客:
https://www.cnblogs.com/LinZhengyu/p/13445696.html
https://www.cnblogs.com/LinZhengyu/p/13451462.html
[JLOI2015]骗我呢
简要题意
给定 \(n,m\),求有多少个 \(n\times m\) 的矩阵,满足:
对于任意的 \(i,j\),都满足矩阵中的第 \(i\) 行第 \(j\) 列的元素 \(x_{i,j}\) 有:
- \(x_{i,j}<x_{i,j+1}(j<m)\);
- \(x_{i,j}<x_{i-1,j-1}(i,j>1)\);
- \(0\le x_{i,j}\le m\)。
结果对 \(10^9+7\) 取模,\(1\le n,m\le 10^6\)。
题解
第 \(1\) 条性质表示这个矩阵中每行都是单调递增的,而第 \(3\) 条性质则限制了每个只有 \(m+1\) 种取值。
我们发现,一行只有 \(m\) 个元素,而每个元素只可能有 \(m+1\) 中取值,且行内单调递增。于是这行有且只有一个在 \([0,m]\) 中的元素没有被取到,而剩下的元素从小到大排序来填充这一行。
于是我们设计 DP 状态 \(f_{i,j}\) 表示进行到第 \(i\) 行,满足第 \(i\) 行缺少的元素时 \(j\) 的方案数。
考虑转移,发现如果 \(k>j+1\) 则对于 \(f_{i,p}=j+1\),就会有 \(f_{i,p}=j+1=f_{i-1,p+1}\),不满足第 \(2\) 条性质。于是要有 \(k\le j+1\),所以有转移:\(f_{i,j}=\sum_{k=1}^{j+1}{f_{i-1,k}}\)。
再优化一下:\(f_{i,j}=\sum_{k=0}^{j+1}{f_{i-1,k}}=\sum_{k=0}^{j}{f_{i-1,k}}+f_{i-1,j+1}=f_{i,j-1}+f_{i-1,j+1}\)。
答案就是 \(f_{n+1,m}\),这样子做是 \(O(nm)\) 的,要考虑优化。
我们考虑这个式子的组合意义,我们先将它映射到坐标轴上。下图中箭头表示转移,而答案就是从 \((1,1)\) 走到 \((n,m)\) 的路径数量。

这里面有些转移时“斜”的,这不太直观。我们将这个网格图变换一下,将第 \(i\) 行的点向右平移 \(i-1\) 格。同时将第 \(1\) 列之间的转移变成先往上再往右走。得到下图:
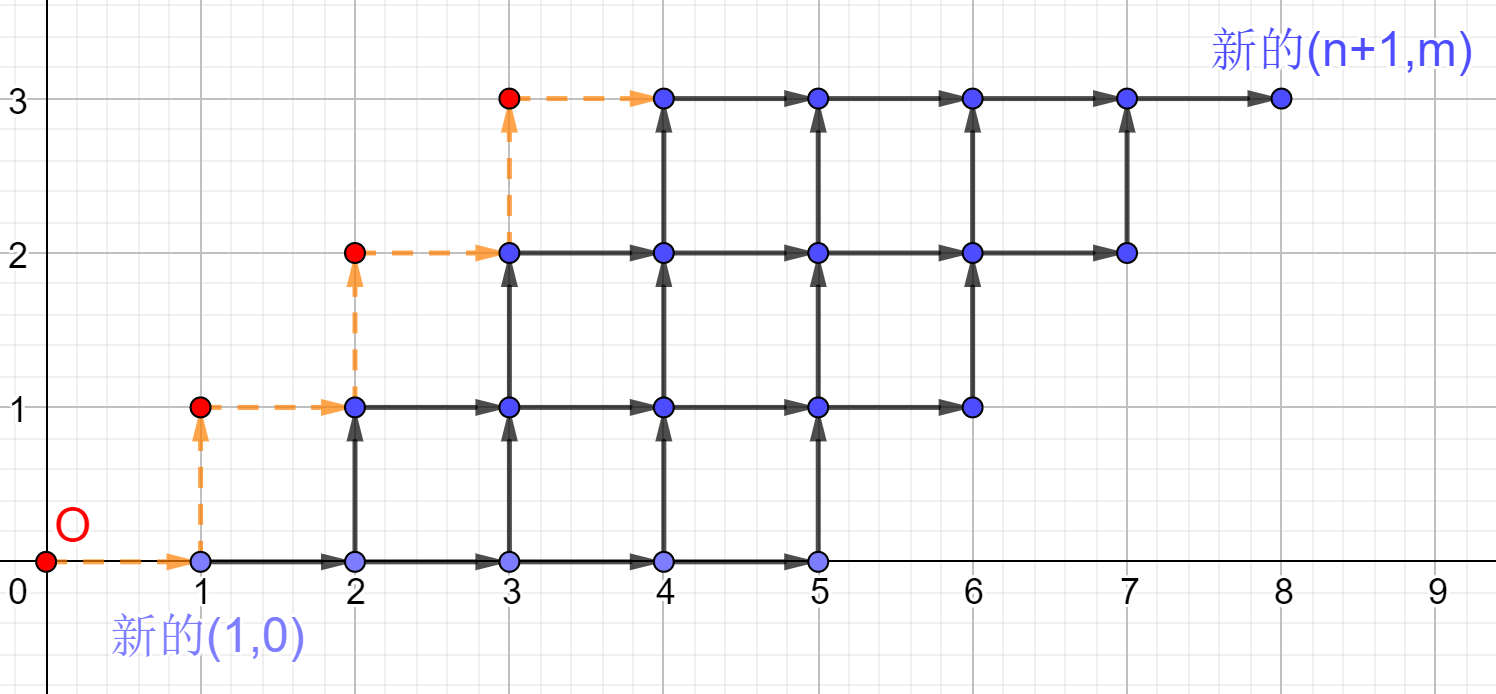
把起点弄到原点上,再画出两条直线:
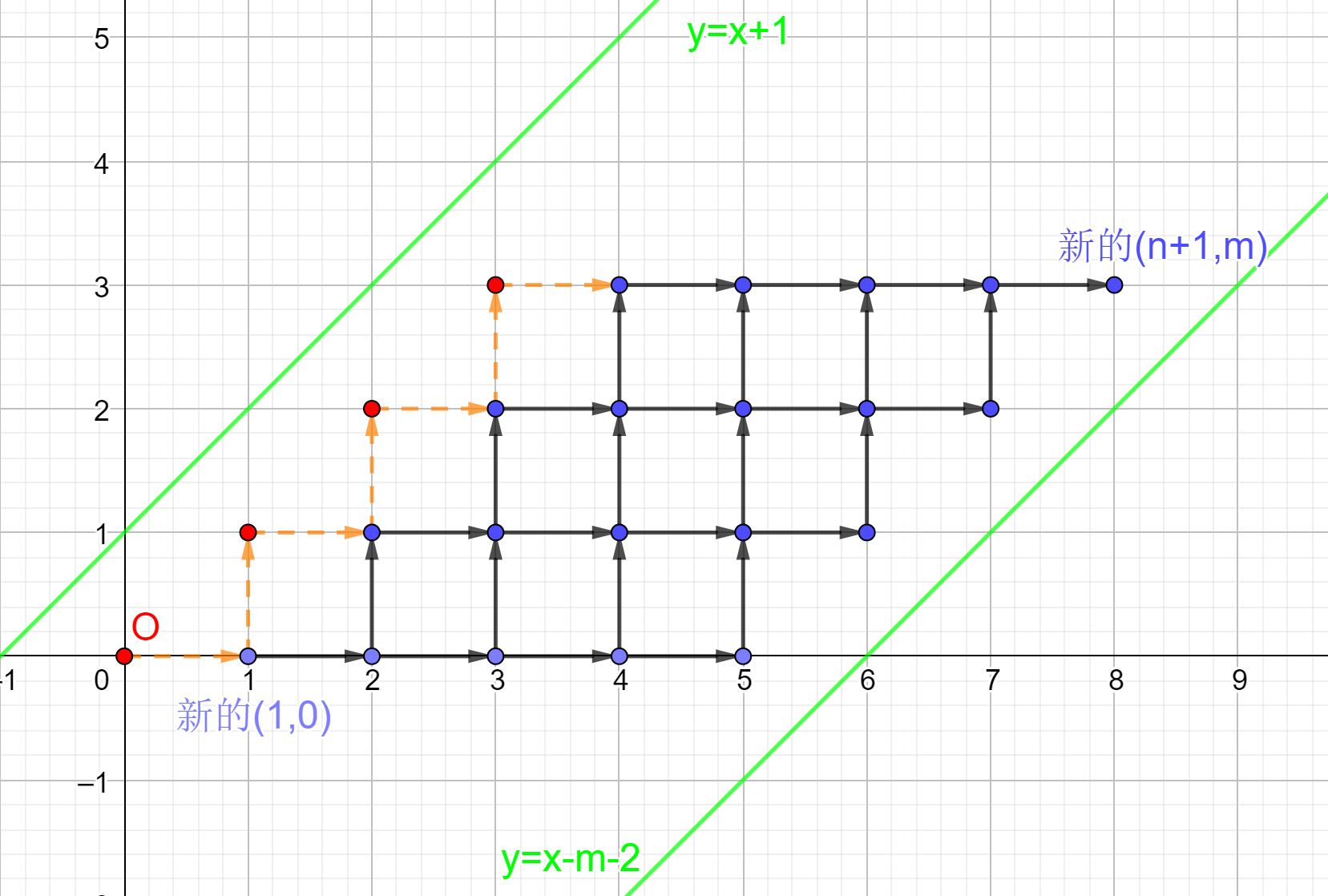
我们发现答案就是从 \((0,0)\) 到 \(T\) 即坐标轴上的 \((n+m+1,n)\) 的路径数量,即只能向右或者向上走,不能触碰到 \(a:y=x+1\) 与 \(b:y=x-m-2\) 两条直线的从 \((0,0)\) 到 \((n+m+1,n)\) 的路径数量。
如果没有两条直线的限制,那么答案显然就是 \(\dbinom {x_T+y_T}{x_T}\)。对于碰到了直线的,例如我们先后触碰到了 \(aabbabb\),发现其实连续触碰到相同的直线之没有上面影响的,可以整个缩起来,于是上面的例子可以被缩为 \(abab\)。
我们回想一下初中奥数“将军饮马”问题,我们发现将 \((n+m+1,n)\) 关于 \(a\) 对称,得到 \(A'\),则从 \((0,0)\) 到 \(A'\) 的每一条路径都和对应的先触碰到 \(a\) 再折回到 \((n+m+1,n)\) 的路径都是一一对应的,数量自然而然也是相等的。这个方法是可以叠加的,例如我们先将 \((n+m+1,n)\) 关于 \(a\) 对称,再关于 \(b\) 对称,则到对应点的路径数则是结尾为 \(ba\) 的路径数。可以见下图:

这样我们就可以计算了。容斥一下,答案就是 \(\dbinom {x_T+y_T}{x_T}-\texttt{先到a的路径数}-\texttt{先到b的路径数}\)。减去先到 \(a\) 的路径数,我们只需要减去以 \(a,ab\) 结尾的方案,加上以 \(ba,bab\) 结尾的方案,减去\(\ldots\)
预处理阶乘的复杂度是线性的;而对称过程,每次的对称距至少增加 \(1\),所以复杂度也是不超过线性的。所以总时间复杂度是线性的,空间复杂度也是线性的。
Code
#include <bits/stdc++.h>
#define il inline
#define ll long long
const int N=3e6+5,P=1e9+7;
int n,m,fac[N],ans;
il int ksm(int a,int b){int res=1; for ( ; b; b>>=1,a=(ll)a*a%P) if (b&1) res=(ll)res*a%P; return res;}
il int C(int x,int y){return x<0||y<0?0:(ll)fac[x+y]*ksm(fac[x],P-2)%P*ksm(fac[y],P-2)%P;}
il void trans(int &x,int &y,int a){std::swap(x,y),x-=a,y+=a;}
int main()
{
scanf("%d%d",&n,&m); int i,x,y;
for (i=fac[0]=1; i<N; i++) fac[i]=(ll)fac[i-1]*i%P;
for (x=n+m+1,y=n,ans=C(x,y); x>=0&&y>=0;) trans(x,y,1),ans=(ans-C(x,y)+P)%P,trans(x,y,-m-2),ans=(ans+C(x,y))%P;
for (x=n+m+1,y=n; x>=0&&y>=0; ) trans(x,y,-m-2),ans=(ans-C(x,y)+P)%P,trans(x,y,1),ans=(ans+C(x,y))%P; printf("%d\n",ans);
return 0;
}
类似题目
简要题意
给定 \(N,m\),对于每个 \(n=1\sim N\),求有多少个长度为 \(2n\) 的环,满足:
- 环中的每个元素都是 \(1\sim m\) 的整数;
- 环上任意相邻的两个数之差的绝对值都是 \(1\)。
结果对 \(998244353\) 取模,\(1\le n,m\le 10^5\)。
题解
有一个显然的 \(O(Nm^2)\) 的 DP 做法,我们枚举起点 \((0,x)\),则终点必是 \((2n,x)\),做一遍 \(O(Nm)\) 的 DP 即可。
我们考虑同上一题一样的,把这些转移放到坐标轴上看,可以发现答案就是从 \((0,x)\) 为起点,只能向右上或者右下走,并且不能碰到直线 \(a:y=0\) 与 \(b:y=m+1\),到 \((2n,x)\) 的路径个数。
同之前一样,做对称变化,得到如下过程:
不翻折的,从 \((0,i)\) 到 \((2n,i)\),贡献是 \(\dbinom {2n}n\cdot m\);
以 \(a\) 或 \(b\) 为中心翻折的,从 \((0,i)\) 到 \((2n,-i)\),贡献是 \(-\sum_{i=1}^m \dbinom {2n}{n+i}\) 的;
以 \(ab\) 或 \(ba\) 为中心翻折的,从 \((0,i)\) 到 \((2n,2m+i+2)\),贡献是 \(\dbinom {2n}{n+m+1}\cdot m\) 的。
\(\ldots\)
你发现,对于 \(\dbinom {2n}i\),只有满足 \(i\equiv n\pmod{m+1}\) 时它的系数是 \(m\),而其他位置的系数都是 \(-1\)。又因为 \(\sum_{i=0}^{2n} \dbinom {2n}i=2^{2n}\),所以答案就是:
这样就可以单次 \(O\left(\dfrac nm\right)\) 计算了。
接下来考虑对 \(m\) 根号分类,对于 \(m>\sqrt{N}\) 的,可以直接用上面的算法做;而对于 \(m\le \sqrt{N}\) 的,我们做一个 DP,维护 \(g_i=\sum\limits_{j\equiv i\pmod{m+1}} \dbinom{n}j\),单次转移时 \(O(m)\) 的,用滚动数组优化空间。
这样子时间复杂度就是 \(O\left(N\sqrt{N}\right)\) 的,空间复杂度是 \(O(N)\) 的。
Code
#include <bits/stdc++.h>
#define il inline
#define ll long long
const int N=2e5+5,P=998244353;
int n,m,o,f[2][N],fac[N],iac[N],mi[N],ans[N];
il int ksm(int a,int b){int res=1; for ( ; b; b>>=1,a=(ll)a*a%P) if (b&1) res=(ll)res*a%P; return res;}
il int C(int x,int y){return x<y||y<0?0:(ll)fac[x]*iac[y]%P*iac[x-y]%P;}
int main()
{
scanf("%d%d%d",&n,&m,&o); int i,j,k=0;
for (i=fac[0]=mi[0]=1; i<N; i++) fac[i]=(ll)fac[i-1]*i%P,mi[i]=2ll*mi[i-1]%P;
for (iac[i=N-1]=ksm(fac[N-1],P-2); i; i--) iac[i-1]=(ll)iac[i]*i%P;
if (m*m<=n)
{
for (f[0][0]=i=1; i<=n+n; i++) for (k^=1,j=0; j<=m; j++)
{
f[k][(j+1)%(m+1)]=(f[!k][j]+f[!k][(j+1)%(m+1)])%P;
if (i&1^1) ans[i>>1]=((ll)f[k][i/2%(m+1)]*(m+1)-mi[i]+P)%P;
}
}
else
{
for (i=1; i<=n; i++)
{
for (j=i%(m+1); j<=i+i; j+=m+1) ans[i]=(ans[i]+C(i+i,j))%P;
ans[i]=((ll)ans[i]*(m+1)-mi[i+i]+P)%P;
}
}
for (i=1; i<=n; i++) if (i==n||o) printf("%d\n",ans[i]);
return 0;
}
另一道类似题目——【集训队作业2018】count
简要题意(照抄原题面)
如果一个序列满足序列长度为 \(n\),序列中的每个数都是 \(1\) 到 \(m\) 内的整数,且所有 \(1\) 到 \(m\) 内的整数都在序列中出现过,则称这是一个挺好序列。
对于一个序列 \(A\),记 \(f_A(l,r)\) 为 \(A\) 的第 \(l\) 个到第 \(r\) 个数中最大值的下标(如果有多个最大值,取下标最小的)。
两个序列 \(A\) 和 \(B\) 同构,当且仅当 \(A\) 和 \(B\) 长度相等,且对于任意 \(i\le j\),均有 \(f_A(i,j)=f_B(i,j)\)。
给出 \(n,m\),求有多少种不同构的挺好序列。答案对 \(998244353\) 取模。
\(1\le n,m\le 10^5\)。
题解
考虑对原序列建出笛卡尔树(不知道笛卡尔树的可以去搜一下),则两个序列同构当且仅当他们的笛卡尔树同构。又由于有 \(m\) 的限制,这转化到树上就是每个叶子到根路径上作为左儿子的点要小于 \(m\)。因为笛卡尔树和序列是一一对应的,于是问题转化为了求有 \(n\) 个节点且最长左链不超过 \(m\) 的笛卡尔树数量。
这个就是经典结论:求有多少条从 \((0,0)\) 出发到 \((2n,0)\) 的路径,满足只能向右上或者右下走,并且不能触碰到 \(y=-1\) 与 \(y=m+1\)。这个直接用之前的方法做即可。
时空复杂度显然都是线性的。
Code
#include <bits/stdc++.h>
#define il inline
#define ll long long
const int N=2e5+5,P=998244353;
int n,m,ans,fac[N];
il int ksm(int a,int b){int res=1; for ( ; b; b>>=1,a=(ll)a*a%P) if (b&1) res=(ll)res*a%P; return res;}
il void flip(int &x,int &y){x=m-x,y=-y-2,std::swap(x,y);}
il int C(int x,int y){return y<0||x<y?0:(ll)fac[x]*ksm(fac[y],P-2)%P*ksm(fac[x-y],P-2)%P;}
int main()
{
scanf("%d%d",&n,&m); if (n<m) return puts("0"),0; n+=n,m+=m+2; int i,x=-2,y=m;
for (fac[0]=i=1; i<N; i++) fac[i]=(ll)fac[i-1]*i%P;
for (i=P-1,ans=C(n,n/2); x>=-n||y<=n; i=P-i,flip(x,y))
ans=(ans+(ll)i*C(n,x+n>>1)+(ll)i*C(n,y+n>>1))%P;
printf("%d\n",ans);
return 0;
}

