2020-07-30 Div.2模拟赛题解
前不久的初二初三互测,由于大佬们都不屑于出题,所以初三就派我出题了。
T1 直线型 Boss 房间的攻略(sao)
题意
给定一个长度为 \(n\) 的整数序列 \(\{d_i\}\),求一个长度为 \(m\) 的整数序列 \(\{p_i\}\),满足:
- \(d_1,d_2,\cdots,d_n,p_1,p_2,\cdots,p_m\) 这 \(n+m\) 个数两两不同;
- 使得式子: \(\sum\limits_{i=1}^{m}{\min\limits_{1\le j\le n}\{|p_i-d_j|\}}\) 的值最小。
对于 \(5\%\) 的数据,\(n,m\le 5\)。
对于 \(20\%\) 的数据,\(n,m\le 1\ 000\)。
另有 \(5\%\) 的数据,满足 \(m=1\)。
另有 \(5\%\) 的数据,满足 \(n=1\)。
对于 \(100\%\) 的数据,\(n,m\le 2\times 10^5,-10^9\le d_i\le 10^9\) ,并且保证 \(d_1,d_2,\cdots,d_n\) 这 \(n\) 个数两两不同。
算法一
枚举距离 \(x\),对于每个点判断到这个点距离为 \(x\) 的点有没有被占用,没有就加入答案。时间复杂度为 \(O(n^2)\),空间复杂度为 \(O(n)\),期望得分 \(20\) 分。
算法二
贪心地,我们肯定优先选择与这 \(n\) 个点距离为一的点,若没有被占用,就加入答案,接着再考虑距离为二的点,以此类推。
发现这其实就是一个BFS的过程,整个数轴就是这张隐式图。于是我们先将这 \(n\) 个点加入队列,然后在隐式图上跑 BFS 即可。判重可以使用哈希表或者 STL 中的 map。时空复杂度均为 \(O(n)\) 或 \(O(n\log{n})\),期望得分 \(100\) 分。
算法三
年仅 \(11\) 岁的大佬hhoppitree提供的解法。
对于这 \(m\) 个点,我们求出 \(\max\limits_{1\le i\le m}\{\min\limits_{1\le j\le n}\{|p_i-d_j|\}\}\),也就是离最近的门最远的距离,我们将其记为 \(g\)。显然我们发现,只有当 \(g\) 达到某一个值的时候,才有可以放置这 \(m\) 个点的方案存在。
我们考虑二分出这个最小的 \(g\),之后就变成了模拟问题,可以直接填数了。时间复杂度为 \(O(n\log{n})\),空间复杂度为 \(O(n)\),期望得分 \(100\) 分。
Code
#include <stdio.h>
#include <unordered_map>
#define int long long
using namespace std;
const int N=2e5+1;
int n,m,c,ans,p[N],q[N+N],h=1,t;
unordered_map<int,int> o;
signed main()
{
freopen("sao.in","r",stdin),freopen("sao.out","w",stdout);
scanf("%lld%lld",&n,&m),c=m; int i,x;
for (i=1; i<=n; i++) scanf("%lld",&x),q[++t]=x,o[x]=0;
while (h<=t)
{
if (!c) break;
x=q[h++];
if (o[x]) ans+=o[x],p[c--]=x;
if (!o.count(x-1)) o[x-1]=o[x]+1,q[++t]=x-1;
if (!o.count(x+1)) o[x+1]=o[x]+1,q[++t]=x+1;
}
for (i=1,printf("%lld\n",ans); i<=m; i++) printf("%lld ",p[i]);
return 0;
}
T2 外界宿的防火墙工程(outlaw)
题意
给定一棵含有 \(n\) 个点的树,对于树上的每条边,求出删掉这条边后两个联通块的直径分别是多少。
对于 \(30\%\) 的数据,保证 \(1 \leq n \leq 5000\)。
对于 \(60\%\) 的数据,保证 \(1 \leq n \leq 4 \times 10^5\)。
对于 \(100\%\) 的数据,保证 \(1 \leq n \leq 4 \times 10^6,0 \leq w \leq 10^6\) 。
算法一
枚举删掉了哪一条边,然后对于两部分暴力求直径,时间复杂度为 \(O(n^2)\),空间复杂度为 \(O(n)\),期望得分 \(30\) 分。
算法二
我们求出一个点 \(u\) 向其不同的儿子走的第一、二、三长链的长度,分别记为 \(first_u,second_u,third_u\),并且记下这三条链分别走的儿子: \(a_u,b_u,c_u\);再记点 \(u\) 向上走的最长链的长度为 \(up_u\) (通过 \(fa\) 走向更远的祖先或到达 \(u\) 的兄弟)。
\(first_u,second_u,third_u,a_u,b_u,c_u\) 可以用一遍自下而上 dfs 求出,这样我们就可以得到切断 \((u,fa)\) 后下半部分的直径 \(P_u\),显然有: \(P_u=first_u+second_u\)。
考虑 \(up_u\) 如何求,我们已经知道了 \(up_{fa}\),从 \(fa\) 转移到 \(u\) 分成三类情况讨论(下面将 \(x+y+z-\min\{x,y,z\}\) 记作 \(cal(x,y,z)\) ):
- 若 \(u=a_{fa}\),则 \(up_u=w(u,fa)+cal(up_{fa},second_{fa},third_{fa})\);
- 若 \(u=b_{fa}\),则 \(up_u=w(u,fa)+cal(up_{fa},first_{fa},third_{fa})\);
- 若 \(u\ne a_{fa}\) 且 \(u\ne b_{fa}\),则 \(up_u=w(u,fa)+cal(up_{fa},first_{fa},second_{fa})\)。
这可以使用一遍自上而下的 dfs 求出。
最后考虑如何求出切断 \((u,fa)\) 后上半部分的直径 \(Q_u\),这和求 \(up_u\) 类似,考虑那些链没有被占用,取其中最大的两个相加即可,当人最后要和 \(Q_{fa}\) 去个 \(\max\),这也可以使用一遍自上而下的 dfs 求出。
所以我们进行自上而下、自下而上两遍 dfs 就可以解决这个问题,时空复杂度均为 \(O(n)\),期望得分 \(100\) 分,注意常数问题。
算法三
同届巨神Dreamunk和Vxlimo提供的解法。
首先我们可以求出原树直径的两个端点,设为 \(root_1\) 和 \(root_2\)。
记 \(f_{root,i}\) 表示以原树直径的某个端点为根,以第 \(i\) 个节点为根的子树的直径大小。
显然删去的边有两种可能,直径边和非直径边,设 \(u\) 为距离 \(root_1\) 更近的端点,\(v\) 为较远的那个。
- 对于非直径边,其中一个分裂后的子树的直径就等于原直径,而另一个子树的直径,即为 \(f_{root_1,v}\)。显然使用 \(f_{root_2,v}\) 也是一样的。
- 对于直径边,容易得到两个子树的直径分别为 \(f_{root_1,v},f_{root_2,u}\)。
遍历每条边(注意不要重复遍历反向边),统计即可。时空复杂度均为 \(O(n)\),期望得分 \(100\) 分。
Code
#include <stdio.h>
#include <algorithm>
#define il inline
#define ll long long
using namespace std;
const int N=4e6+1;
const ll mod=2333333333333333ll;
int n,son[3][N]; ll ans;
int to[N+N],nx[N+N],wt[N+N],head[N],sze;
ll P[N],Q[N],mxl[3][N],up[N];
il char gc()
{
static char now[1<<20],*S,*T;
if (T==S)
{
T=(S=now)+fread(now,1,1<<20,stdin);
if (T==S) return EOF;
}
return *S++;
}
il int read()
{
int res; char c;
while ((c=gc())<'0'||c>'9'); res=c^48;
while ((c=gc())>='0'&&c<='9') res=(res<<3)+(res<<1)+(c^48);
return res;
}
il ll cal(ll x,ll y,ll z){return x+y+z-min(x,min(y,z));}
il void add(int u,int v,int w){to[++sze]=v,nx[sze]=head[u],wt[sze]=w,head[u]=sze;}
il void dfs1(int u,int F)
{
ll l1=0,l2=0,l3=0; int i,v,w,s1=0,s2=0,s3=0;
for (i=head[u]; i; i=nx[i])
{
if ((v=to[i])==F) continue;
w=wt[i],dfs1(v,u),P[u]=max(P[u],P[v]);
if (mxl[0][v]+1ll*w>l1) s3=s2,s2=s1,s1=v,l3=l2,l2=l1,l1=mxl[0][v]+1ll*w;
else if (mxl[0][v]+1ll*w>l2) s3=s2,s2=v,l3=l2,l2=mxl[0][v]+1ll*w;
else if (mxl[0][v]+1ll*w>l3) s3=v,l3=mxl[0][v]+1ll*w;
}
mxl[0][u]=l1,mxl[1][u]=l2,mxl[2][u]=l3;
son[0][u]=s1,son[1][u]=s2,son[2][u]=s3;
P[u]=max(P[u],l1+l2);
}
il void dfs2(int u,int F)
{
ll l1=0,l2=0; int i,v,w,s1=0,s2=0;
for (i=head[u]; i; i=nx[i])
{
if ((v=to[i])==F) continue; w=wt[i];
if (P[v]>l1) s2=s1,s1=v,l2=l1,l1=P[v];
else if (P[v]>l2) s2=v,l2=P[v];
if (v==son[0][u]) up[v]=1ll*w+max(up[u],mxl[1][u]),Q[v]=max(Q[u],cal(up[u],mxl[1][u],mxl[2][u]));
else
{
up[v]=1ll*w+max(up[u],mxl[0][u]);
if (v==son[1][u]) Q[v]=max(Q[u],cal(up[u],mxl[0][u],mxl[2][u]));
else Q[v]=max(Q[u],cal(up[u],mxl[0][u],mxl[1][u]));
}
}
for (i=head[u]; i; i=nx[i])
{
if ((v=to[i])==F) continue;
if (v==s1) Q[v]=max(Q[v],l2);
else Q[v]=max(Q[v],l1);
dfs2(v,u);
}
}
il void getans(int u,int F)
{
int i,v;
for (i=head[u]; i; i=nx[i]) if ((v=to[i])!=F)
ans=(ans+23333ll*max(P[v],Q[v])+2333ll*min(P[v],Q[v]))%mod,getans(v,u);
}
int main()
{
freopen("outlaw.in","r",stdin),freopen("outlaw.out","w",stdout);
n=read(); int i,u,v,w;
for (i=1; i<n; i++)
{
u=read(),v=read(),w=read(),add(u,v,w),add(v,u,w);
ans=(ans+233ll*i*i+23ll*i+2ll)%mod;
}
dfs1(1,0),dfs2(1,0);
getans(1,0),printf("%lld",ans);
return 0;
}
T3 为美丽的阿克塞尔献上爆裂烟火(explosion)
题意
在平面上有一个以原点为圆心半径为 \(r\) 的圆和 \(n\) 个点。对于任意两个不同点 \(u,v\),他们之间有连边当且仅当过 \(u,v\) 的直线与给定的圆没有交,求这 \(n\) 组成的图的最大团(极大完全子图)。
对于 \(10\%\) 的数据,\(n\le 20\)。
对于 \(30\%\) 的数据,\(n\leq 100\)。
对于 \(100\%\) 的数据,\(1\le n \le 2\ 000,|x_i|,|y_i|,R \le 5\ 000\) ,并且保证每个魔晶石都严格在城外,没有重合点,且两两连线不与城墙相切。
算法一
对于每个点分为在或者不在最大团中暴力搜索,时间复杂度为 \(O(2^n)\),空间复杂度为 \(O(n)\),期望得分 \(10\) 分。
算法二
我们过一个点 \(i\) 向圆引两条切线,切出两段圆弧,我们取出为劣弧的那一段,这也可以理解为光源照亮圆的部分,将这段极角区间记为 \([l_i,r_i]\)。通过画图,我们可以发现,对于任意两个点 \(i,j\),当且仅当 \([l_i,r_i]\) 与 \([l_j,r_j]\) 这两段区间有交但是不是包含关系的时候,过这两个点的直线与圆才没有交,证明显然。
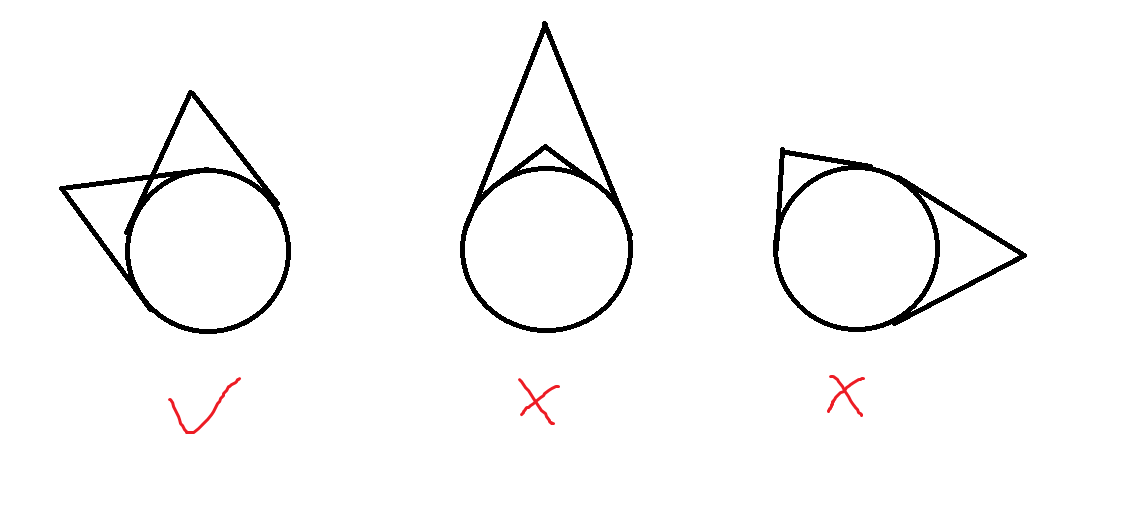
那么我们发现,对于一个团 \(\{a_1,a_2,\cdots,a_k\}\),要满足:
若按照 \(l\) 为关键字从小到大排序,则有:
- 对于任意 \(1\le i\le k\),都有 \(l_1\le l_{a_i}\le r_1\);
- 对于任意 \(1\le j<i\le k\),都有 \(r_{a_j}<r_{a_i}\)。
我们枚举一个点 \(i\),假设其在最大团中,则我们将所有左端点在区间 \([l_i,r_i]\) 的点加进来,然后以 \(l\) 为关键从小到大排完序后求一遍关于 \(r\) 的最长上升子序列的长度就可以了,最后取 \(1\) 到 \(n\) 的最大值。
枚举复杂度为 \(O(n)\),求 LIS 复杂度为 \(O(n\log{n})\),所以总复杂度为 \(O(n^2\log{n})\)(当然如果你用 \(O(n^2)\) 的复杂度求 LIS 的话就会获得 \(30\) 分的好成绩),空间复杂度为 \(O(n)\),期望得分 \(100\) 分 (30分)。
Code
#include <stdio.h>
#include <math.h>
#include <algorithm>
#define il inline
#define db double
using namespace std;
const int N=2001;
const db pi=acos(-1.0);
int n,ans; db CR;
struct node{db x,y;}P[N];
db l[N],r[N],rr[N],lis[N],L,R;
int T,A[N],ok[N];
il bool bh(db l,db r,db x)
{
if (l<r) return l<x&&x<r;
return (x>l)||(x<r);
}
il bool cmp1(int a,int b){return l[a]<l[b];}
il bool cmp2(int a,int b)
{
if (a>L&&b>L||a<R&&b<R) return l[a]<l[b];
return l[a]>L;
}
il int find(int x,int len)
{
int le=1,ri=len,mid;
while (le<ri)
{
mid=le+ri>>1;
if (lis[mid]>=rr[x]) ri=mid;
else le=mid+1;
}
return le;
}
il int LIS()
{
int i,res=1;
for (i=1; i<=A[0]; i++)
{
rr[i]=r[A[i]]-L;
if (rr[i]<0) rr[i]+=2*pi;
}
for (i=2,lis[1]=rr[1]; i<=A[0]; i++)
{
if (rr[i]>lis[res]) lis[++res]=rr[i];
else lis[find(i,res)]=rr[i];
}
return res;
}
int main()
{
freopen("explosion.in","r",stdin),freopen("explosion.out","w",stdout);
scanf("%d%lf",&n,&CR); int i,j; db AZ,del;
for (i=1; i<=n; i++) scanf("%lf%lf",&P[i].x,&P[i].y);
for (i=1; i<=n; i++)
{
AZ=atan2(P[i].y,P[i].x),del=fabs(acos(CR/sqrt(P[i].x*P[i].x+P[i].y*P[i].y)));
l[i]=AZ-del,r[i]=AZ+del;
if (l[i]<-pi) l[i]+=pi*2;
if (r[i]>pi) r[i]-=pi*2;
}
for (i=T=1; i<=n; i++,T++)
{
for (j=1,A[A[0]=1]=i; j<=n; j++)
{
if (i!=j&&bh(l[i],r[i],l[j])&&!bh(l[i],r[i],r[j])) A[++A[0]]=j;
else if (i!=j&&bh(l[i],r[i],r[j])&&!bh(l[i],r[i],l[j])) swap(l[j],r[j]),A[++A[0]]=j,ok[j]=T;
}
L=l[i],R=r[i],sort(A+1,A+A[0]+1,L<R?cmp1:cmp2),ans=max(ans,LIS());
for (j=1; j<=A[0]; j++) if (ok[j]==T) swap(l[j],r[j]);
}
printf("%d",ans);
return 0;
}
T4 关于梅普露的盾牌被打破了这件事(overvit)
题意
给定一个大小为 \(n\times m\) 的自然数矩阵 \(A\),求一个大小也为 \(n\times m\)的整数矩阵 \(B\),满足:
- 对于任意 \(i,j\),都有 \(B_{i,j}\in [L,R]\);
- 使得 \(\max\{\max\limits_{1\le j\le m}\{|\sum\limits_{i=1}^{n}{A_{i,j}-B_{i,j}}|\},\max\limits_{1\le i\le n}\{|\sum\limits_{j=1}^{m}{A_{i,j}-B_{i,j}}|\}\}\) 最小。
对于 \(20\%\) 的数据,满足 \(1\le n,m\le 20\)。
对于另外 \(20\%\) 的数据,满足 \(0\le L\le R\le 1\)。
对于 \(100\%\) 的数据,满足 \(1\le n,m\le 200;0\le L\le R\le 1\ 000;0\le A_{i,j}\le 1000\)。
算法一
暴力搜索每个位置填什么数,时间复杂度为 \(O(2^{nm})\),空间复杂度为 \(O(nm)\),加上剪枝有奇效,期望得分 \(0\sim 10\) 分。
算法二
二分答案,转为判定性问题,设当前二分值为 \(ans\)。
考虑网络流,我们从第 \(i\) 行向第 \(j\) 列连边,下界为 \(L\),上界为 \(R\),表示 \(B_{i,j}\in [L,R]\);从超级源点向第 \(i\) 列连边,下界 \(\max\{0,U_i-ans\}\),上界为 \(U_i+ans\),\(U_i=\sum\limits_{j=1}^m{A_{i,j}}\),表示 \(|\sum\limits_{j=1}^{m}{A_{i,j}-B_{i,j}}|\le ans\),列同理。
建完边后,跑一边有源汇上下界可行流即可。方案的输出就是考虑当存在可行流时,\(B_{i,j}\) 就等于从第 \(i\) 行向第 \(j\) 列连的边的流量。
复杂度是 \(O(N^2M\log)\) 的,其中 \(N,M\) 分别为流网络图中的点数和边数,空间复杂度为 \(O(N+M)\),期望得分 \(100\) 分。
Code
#include <stdio.h>
#include <algorithm>
#define il inline
#define int long long
using namespace std;
const int N=201,M=265000;
int n,m,L,R,ans,A[N][N],U[N],V[N];
int to[M],nx[M],cap[M],head[M],sze;
int S,T,h,t,q[M],it[M],lev[M];
il void add(int u,int v,int c){to[++sze]=v,nx[sze]=head[u],cap[sze]=c,head[u]=sze;}
il void adde(int u,int v,int c){add(u,v,c),add(v,u,0);}
il void addlr(int u,int v,int l,int r){adde(S,v,l),adde(u,T,l),adde(u,v,r-l);}
il int bfs()
{
int i,u,v;
for (i=1; i<=n+m+4; i++) lev[i]=0;
q[h=t=lev[S]=1]=S;
while (h<=t)
for (i=head[u=q[h++]]; i; i=nx[i])
if (cap[i]&&!lev[v=to[i]]) lev[v]=lev[u]+1,q[++t]=v;
return lev[T];
}
il int dfs(int u,int f)
{
if (u==T) return f; int z,res=0;
for (int &i=it[u]; i; i=nx[i])
if (cap[i]&&lev[to[i]]==lev[u]+1&&(z=dfs(to[i],min(f-res,cap[i]))))
{
cap[i]-=z,cap[i^1]+=z,res+=z;
if (res==f) break;
}
return res;
}
il int dinic()
{
int i,res=0,f;
while (bfs())
{
for (i=1; i<=n+m+4; i++) it[i]=head[i];
while (f=dfs(S,1e9)) res+=f;
}
return res;
}
il int check(int x)
{
sze=1; int i,j,okf=0;
for (i=1; i<=n+m+4; i++) head[i]=0;
for (i=1; i<=n; i++) for (j=1; j<=m; j++) addlr(i+4,n+j+4,L,R),okf+=L;
for (i=1; i<=n; i++) addlr(3,i+4,max(U[i]-x,0ll),U[i]+x),okf+=max(U[i]-x,0ll);
for (j=1; j<=m; j++) addlr(n+j+4,4,max(V[j]-x,0ll),V[j]+x),okf+=max(V[j]-x,0ll);
addlr(4,3,0ll,1e9);
return dinic()==okf;
}
signed main()
{
freopen("overvit.in","r",stdin),freopen("overvit.out","w",stdout);
scanf("%d%d",&n,&m),S=1,T=2; int i,j,p=1,l=0,r=2e5,mid;
for (i=1; i<=n; i++) for (j=1; j<=m; j++) scanf("%d",A[i]+j);
scanf("%d%d",&L,&R);
for (i=1; i<=n; i++) for (j=1; j<=m; j++) U[i]+=A[i][j];
for (j=1; j<=m; j++) for (i=1; i<=n; i++) V[j]+=A[i][j];
while (l<=r)
{
mid=l+r>>1;
if (check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
printf("%lld\n",ans),check(ans);
for (i=1; i<=n; puts(""),i++) for (j=1; j<=m; j++) p+=6,printf("%lld ",cap[p]+L);
return 0;
}

