数据预处理|8.聚类分析
8.1 聚类模型
由于你已经学会了如何在数据分析中执行预测和分类任务,在本章中,你将学习聚类分析。在聚类中,我们努力对数据集中的数据对象进行有意义的分组。我们将通过一个例子来学习聚类分析。
8.1.1 使用二维数据集进行聚类的例子
在这个例子中,我们将使用WH Report_preprocessed.csv,根据2019年名为Life_Ladder和Perceptions_of_corruption的两个分数对各国进行聚类。
下面的代码将数据读入report_df,并使用布尔掩码将数据集预处理为report2019_df,其中只包括2019年的数据。
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
report_df = pd.read_csv('https://raw.githubusercontent.com/PacktPublishing/Hands-On-Data-Preprocessing-in-Python/main/Chapter08/WH%20Report_preprocessed.csv')
BM = report_df.year == 2019
report2019_df = report_df[BM]
report2019_df.head()
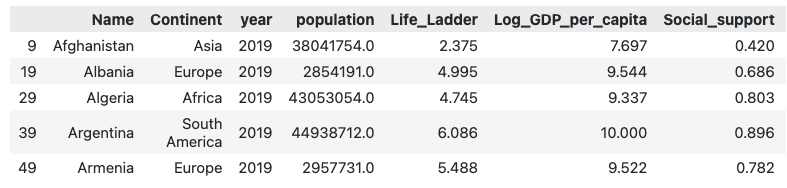
前面代码的结果是,我们有一个DataFrame,report2019_df,其中只包括2019年的数据,正如提示所要求的。
由于我们只有两个维度来进行聚类,我们可以利用散点图来显示所有国家在有关的两个属性基础上的相互关系。生命阶梯和对腐败的看法。
下面的代码分两步创建散点图。
- 按照我们在第5章 "数据可视化 "中学到的方法创建散点图。
- 循环浏览report2019_df中的所有数据对象,用plt.annotate()注释散点图中的每个点。
plt.figure(figsize=(12,12))
plt.scatter(report2019_df.Life_Ladder,report2019_df.Perceptions_of_corruption)
for _,row in report2019_df.iterrows():
plt.annotate(row.Name,(row.Life_Ladder,row.Perceptions_of_corruption))
plt.xlabel('Life_Ladder')
plt.ylabel('Perceptions_of_corruption')
plt.show()

由于数据只有两个维度,我们只需看一下前述的图,就可以看到基于生活阶梯和腐败感的国家组之间有更多的相似之处。例如,下图描述了基于前述散点图的国家组。在一个以上群组边界内的国家应被分配到其中一个群组。
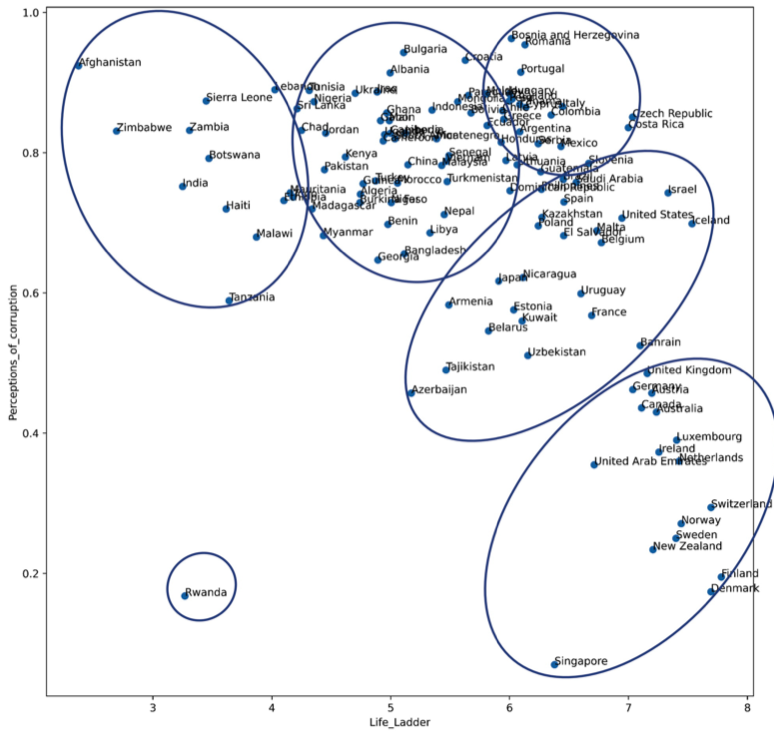
在这里,我们看到,我们可以将数据集中的所有国家有意义地分成六个群组。其中一个聚类只有一个数据对象,表明该数据对象是基于 "生活阶梯 "和 "腐败感知 "属性的异常值。
这里的关键术语是有意义的聚类。因此,让我们用这个例子来理解我们所说的有意义的聚类是什么意思。前面图中所示的六个聚类是有意义的,原因如下。
- 处于同一聚类中的数据对象在 "生活阶梯 "和 "对腐败的看法 "中的数值相似。
- 处于不同聚类中的数据对象在 "生活阶梯 "和 "对腐败的看法 "中具有不同的数值。
总之,有意义的聚类意味着聚类的方式是相同聚类的成员相似,而不同聚类的成员则不同。
当我们在两个维度上进行聚类时,意味着我们只有两个属性,聚类的任务很简单,如前面的例子所示。然而,当维度的数量增加时,我们用可视化的方式看到数据之间的模式的能力就会下降或者变得不可能。
例如,在下面的例子中,我们将了解到当我们有两个以上的属性时,可视化聚类的难度。
8.1.2 使用三维数据集进行聚类的例子
在这个例子中,我们将使用WH Report_preprocessed.csv。尝试在2019年根据三个幸福指数对国家进行聚类,这三个幸福指数被称为 "生活阶梯"、"腐败感知 "和 "慷慨"。
下面的代码创建了一个散点图,使用颜色来增加第三个维度。
plt.figure(figsize=(12,12))
plt.scatter(report2019_df.Life_Ladder,report2019_df.Perceptions_of_corruption,c=report2019_df.Generosity,cmap='binary')
plt.xlabel('Life_Ladder')
plt.ylabel('Perceptions_of_corruption')
plt.show()
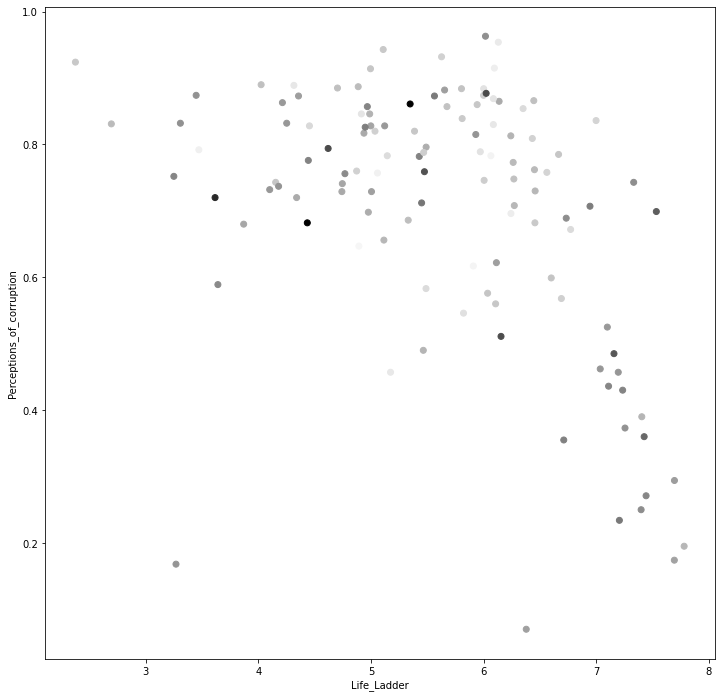
运行前面的代码将创建下图。下图将 "生命阶梯 "作为X维度,将 "对腐败的看法 "作为Y维度,将 "慷慨 "作为颜色。标记越浅,慷慨度得分越低,而标记越深,慷慨度得分越高。
试着用前面的可视化方法,根据三个属性一次性找到有意义的数据对象聚类。这项任务对我们来说将是不堪重负的,因为我们的大脑并不擅长执行需要同时处理两个以上维度的任务。
前面的图没有包括国家的名称,因为即使没有这些名称,我们也很难用这个图来进行聚类。加入国家标签只会让我们更加不知所措。
这个例子的目的不是为了完成它,但我们得出的结论非常重要:当数据有两个以上的维度时,我们需要依靠数据可视化以外的工具和我们的大脑来进行有意义的聚类。
我们用于高维聚类的工具是算法和计算机。
有许多不同类型的聚类算法,有各种工作机制。
在本章中,我们将了解最流行的聚类算法。K-Means。这种算法简单、可扩展,而且对聚类很有效。
8.2 K-均值算法
K-Means是一种基于随机的启发式聚类算法。基于随机的意思是,算法在同一数据上的输出在每次运行时都可能不同,而启发式的意思是,算法并没有达到最优解。然而,根据经验,我们知道它能达到一个好的解决方案。
K-Means使用一个简单的循环对数据对象进行聚类。下图显示了该算法所执行的步骤,以及启发式地在数据中寻找聚类的循环。

我们可以看到,该算法首先随机选择k个数据对象作为聚类中心点。然后,数据对象被分配到最接近其中心点的聚类中。
接下来,中心点通过集群中所有数据对象的平均值进行更新。随着中心点的更新,数据对象被重新分配到最接近其中心点的集群。现在,随着聚类的更新,中心点将被更新为聚类中所有新数据对象的平均值。这最后两个步骤不断发生,直到更新中心点后集群没有变化。一旦达到这个稳定性,该算法就会终止。
从编码的角度来看,应用K-means与应用我们迄今为止所了解的任何其他算法非常相似。
8.2.1 使用K-Means对一个二维数据集进行聚类
在本章早些时候,我们利用 "生活阶梯 "和 "腐败感知 "将各国分为六个群组。这里,我们想用K-Means来确认同样的聚类。
下面的代码使用sklearn.cluster模块中的KMeans函数来进行这种聚类。
前面的代码用四行来执行KMeans聚类。
- dimensions = ['Life_Ladder', 'Perceptions_of_corruption']: 这一行代码指定了我们要用于聚类的数据的属性。
- Xs = report2019_df[dimensions]。这行代码分离了我们要用于聚类的数据。
- kmeans = KMeans(n_clusters=6)。这行代码创建了一个K-Means模型,准备将输入的数据聚类为六个簇。
- kmeans.fit(Xs)。这一行代码将我们想要聚类的数据集引入到我们在上一步创建的模型中。
from sklearn.cluster import KMeans
dimensions = ['Life_Ladder','Perceptions_of_corruption']
Xs = report2019_df[dimensions]
kmeans = KMeans(n_clusters=6)
kmeans.fit(Xs)
#每一行的聚类成员可以通过kmeans.labels_访问
for i in range(6):
BM = kmeans.labels_ == i
print('Cluster {}: {}'.format(i,report2019_df[BM].Name.values))
'''
Cluster 0: ['Australia' 'Austria' 'Bahrain' 'Canada' 'Denmark' 'Finland' 'Germany'
'Iceland' 'Ireland' 'Israel' 'Luxembourg' 'Netherlands' 'New Zealand'
'Norway' 'Sweden' 'Switzerland' 'United Kingdom']
Cluster 1: ['Chad' 'Ethiopia' 'Jordan' 'Kenya' 'Lebanon' 'Madagascar' 'Malawi'
'Mauritania' 'Myanmar' 'Nigeria' 'Pakistan' 'Sri Lanka' 'Togo' 'Tunisia']
Cluster 2: ['Argentina' 'Belarus' 'Bolivia' 'Bosnia and Herzegovina' 'Chile'
'Croatia' 'Cyprus' 'Dominican Republic' 'Ecuador' 'Estonia' 'Greece'
'Guatemala' 'Honduras' 'Hungary' 'Japan' 'Kazakhstan' 'Kuwait' 'Latvia'
'Lithuania' 'Moldova' 'Mongolia' 'Nicaragua' 'Panama' 'Paraguay' 'Peru'
'Philippines' 'Poland' 'Portugal' 'Romania' 'Serbia' 'Thailand'
'Uzbekistan']
Cluster 3: ['Albania' 'Algeria' 'Armenia' 'Azerbaijan' 'Bangladesh' 'Benin'
'Bulgaria' 'Burkina Faso' 'Cambodia' 'Cameroon' 'China' 'Gabon' 'Georgia'
'Ghana' 'Guinea' 'Indonesia' 'Iraq' 'Liberia' 'Libya' 'Malaysia' 'Mali'
'Montenegro' 'Morocco' 'Nepal' 'Niger' 'Senegal' 'South Africa'
'Tajikistan' 'Turkey' 'Turkmenistan' 'Uganda' 'Ukraine' 'Vietnam']
Cluster 4: ['Afghanistan' 'Botswana' 'Haiti' 'India' 'Rwanda' 'Sierra Leone'
'Tanzania' 'Zambia' 'Zimbabwe']
Cluster 5: ['Belgium' 'Brazil' 'Colombia' 'Costa Rica' 'Czech Republic' 'El Salvador'
'France' 'Italy' 'Malta' 'Mexico' 'Saudi Arabia' 'Singapore' 'Slovenia'
'Spain' 'United Arab Emirates' 'United States' 'Uruguay']
'''
下面的截图将前面两段代码放在一起,也显示了代码的输出。运行该代码后,你可能会得到与下面截图中所示不同的输出。如果你运行同样的代码几次,你每次都会得到不同的输出。
造成这种不一致的原因是,K-Means是一种基于随机的算法。请参考K-Means流程图:K-Means首先随机选择k个数据对象作为初始中心点。由于这个初始化是随机的,所以输出结果是彼此不同的。
尽管输出结果不同,但每次都是相同的国家被归入同一聚类下。例如,请注意,英国和加拿大每次都在同一个群组中。这是令人欣慰的;这意味着K-Means在数据中找到了相同的模式,尽管它遵循随机程序。
现在,让我们比较一下我们用K-Means找到的聚类和我们用可视化找到的聚类。这些聚类是不同的,尽管用于聚类的数据是相同的。例如,虽然卢旺达在8.2第二幅图中是一个离群点,但在上面的代码输出中却是一个集群的成员。为什么会出现这种情况?在继续阅读之前,请思考一下这个问题。
下面的代码将输出一个视觉,可以帮助你回答这个问题。
plt.figure(figsize=(21,4))
plt.scatter(report2019_df.Life_Ladder,report2019_df.Perceptions_of_corruption)
for _, row in report2019_df.iterrows():
plt.annotate(row.Name,(row.Life_Ladder,row.Perceptions_of_corruption),rotation=90)
plt.xlim([2.3,7.8])
plt.xlabel('Life_Ladder')
plt.ylabel('Perceptions_of_corruption')
plt.show()

前面的输出与图8.1和图8.2的唯一区别是,在前面的输出中,生命阶梯和对腐败的看法的数字刻度已被调整为相同。
Matplotlib自动缩放了图8.1和图8.2的两个维度--"生命之梯 "和 "对腐败的看法",使它们看起来具有相似的视觉范围。如果你注意一下生命阶梯维度上3和4之间的视觉空间量,然后再与感知腐败维度上0.2和0.4之间的视觉空间量进行比较,就可以看出这一点。因此,我们可以看到,虽然视觉空间的数量相等,但代表它们的数值却非常不同。这一认识回答了前面提出的问题:为什么KMeans的聚类结果与我们在图8.2中直观检测到的完全不同?答案是,这两个聚类使用的不是同一个数据。图8.2中表示的聚类使用的是按比例的数据,而Kmeans中表示的聚类(K-Means聚类)使用的是原始数据。
现在,我们需要回答的第二个问题是,我们应该使用哪个聚类输出? 让我来帮助你得出正确的答案。当我们想用两个维度对我们的数据对象进行聚类时,即Life_Ladder和Perceptions_of_corruption,我们希望每个维度在聚类结果中发挥多大的作用?难道我们不希望两个属性发挥同等的作用吗?是的,情况就是这样。所以,我们要选择对两个维度都给予同等重视的聚类。由于K-Means聚类使用的是原始数据,没有对其进行缩放,因此,"生命之梯 "恰好拥有更大的数字,这影响了K-Means将 "生命之梯 "置于 "腐败感知 "之上。
为了克服这一挑战,在应用K-Means或其他以数据对象之间的距离作为重要决定因素的算法之前,我们需要对数据进行归一化处理。归一化数据意味着以这样一种方式重新调整属性,使所有的属性都在同一范围内表示。例如,你可能还记得,在前一章中,我们在应用KNN之前,出于同样的原因,对我们的数据集进行了归一化。
下面的截图显示了在使用K-Means之前对数据集进行标准化处理时的代码和聚类输出。在这段代码中,Xs=(Xs-Xs.min())/(Xs.min()-Xs.max())用于将Xs中的所有属性重新划分为0和1之间。
其余的算法代码与我们在本章前面尝试的代码相同。现在,你可以将下面的截图中的聚类结果与图8.2所示的聚类结果进行比较,以发现这两种聚类方式所取得的结果几乎相同。
from sklearn.cluster import KMeans
dimensions = ['Life_Ladder','Perceptions_of_corruption']
Xs = report2019_df[dimensions]
Xs = (Xs-Xs.min())/(Xs.max()-Xs.min())
kmeans = KMeans(n_clusters=6)
kmeans.fit(Xs)
for i in range(6):
BM = kmeans.labels_ == i
print('Cluster {}: {}'.format(i,report2019_df[BM].Name.values))
'''
Cluster 0: ['Argentina' 'Bolivia' 'Bosnia and Herzegovina' 'Brazil' 'Chile'
'Colombia' 'Costa Rica' 'Croatia' 'Cyprus' 'Czech Republic'
'Dominican Republic' 'Ecuador' 'Greece' 'Guatemala' 'Honduras' 'Hungary'
'Italy' 'Latvia' 'Lithuania' 'Mexico' 'Moldova' 'Mongolia' 'Panama'
'Paraguay' 'Peru' 'Philippines' 'Portugal' 'Romania' 'Saudi Arabia'
'Serbia' 'Slovenia' 'Thailand']
Cluster 1: ['Australia' 'Austria' 'Canada' 'Denmark' 'Finland' 'Germany' 'Ireland'
'Luxembourg' 'Netherlands' 'New Zealand' 'Norway' 'Singapore' 'Sweden'
'Switzerland' 'United Arab Emirates' 'United Kingdom']
Cluster 2: ['Afghanistan' 'Botswana' 'Chad' 'Ethiopia' 'Haiti' 'India' 'Lebanon'
'Malawi' 'Mauritania' 'Sierra Leone' 'Sri Lanka' 'Tanzania' 'Togo'
'Tunisia' 'Zambia' 'Zimbabwe']
Cluster 3: ['Albania' 'Algeria' 'Bangladesh' 'Benin' 'Bulgaria' 'Burkina Faso'
'Cambodia' 'Cameroon' 'China' 'Gabon' 'Georgia' 'Ghana' 'Guinea'
'Indonesia' 'Iraq' 'Jordan' 'Kenya' 'Liberia' 'Libya' 'Madagascar'
'Malaysia' 'Mali' 'Montenegro' 'Morocco' 'Myanmar' 'Nepal' 'Niger'
'Nigeria' 'Pakistan' 'Senegal' 'South Africa' 'Turkey' 'Turkmenistan'
'Uganda' 'Ukraine' 'Vietnam']
Cluster 4: ['Rwanda']
Cluster 5: ['Armenia' 'Azerbaijan' 'Bahrain' 'Belarus' 'Belgium' 'El Salvador'
'Estonia' 'France' 'Iceland' 'Israel' 'Japan' 'Kazakhstan' 'Kuwait'
'Malta' 'Nicaragua' 'Poland' 'Spain' 'Tajikistan' 'United States'
'Uruguay' 'Uzbekistan']
'''
在这个例子中,我们看到了K-Means,如果应用得当,与我们使用数据可视化达到的效果相比,可以产生有意义的聚类。然而,这个例子中的K-Means聚类是应用于一个二维数据集。在下一个例子中,我们将看到,从编码的角度来看,将K-Means应用于二维数据集和将该算法应用于更多维度的数据集之间几乎没有区别。
8.2.2 使用K-Means对两维以上的数据集进行聚类
在本节中,我们将使用K-Means,根据所有的生命阶梯、人均GDP对数、社会支持、出生时健康预期寿命、做出生活选择的自由、慷慨、对腐败的看法、积极影响和消极影响的幸福指数,在2019_df报告中形成三个有意义的国家群组。
继续运行以下代码;你会看到它将形成三个有意义的集群,并打印出每个集群的成员。
这里,前面的代码和代码:8.1中的代码的唯一区别是第一行,在这里选择数据的尺寸。在这之后,代码是相同的。原因是K-Means可以处理输入的尽可能多的维度。
from sklearn.cluster import KMeans
dimensions = ['Life_Ladder','Log_GDP_per_capita','Social_support', 'Healthy_life_expectancy_at_birth', 'Freedom_to_make_life_choices', 'Generosity', 'Perceptions_of_corruption', 'Positive_affect', 'Negative_affect']
Xs = report2019_df[dimensions]
Xs = (Xs-Xs.min())/(Xs.max()-Xs.min())
kmeans = KMeans(n_clusters=3)
kmeans.fit(Xs)
for i in range(3):
BM = kmeans.labels_ == i
print('Cluster {}: {}'.format(i,report2019_df[BM].Name.values))
'''
Cluster 0: ['Albania' 'Algeria' 'Argentina' 'Armenia' 'Azerbaijan' 'Belarus'
'Belgium' 'Bolivia' 'Bosnia and Herzegovina' 'Botswana' 'Brazil'
'Bulgaria' 'Chile' 'China' 'Colombia' 'Costa Rica' 'Croatia' 'Cyprus'
'Czech Republic' 'Dominican Republic' 'Ecuador' 'El Salvador' 'Georgia'
'Greece' 'Guatemala' 'Honduras' 'Hungary' 'Indonesia' 'Israel' 'Italy'
'Japan' 'Kazakhstan' 'Kuwait' 'Latvia' 'Libya' 'Lithuania' 'Malaysia'
'Malta' 'Mexico' 'Moldova' 'Mongolia' 'Montenegro' 'Nicaragua' 'Panama'
'Paraguay' 'Peru' 'Philippines' 'Poland' 'Portugal' 'Romania'
'Saudi Arabia' 'Serbia' 'Slovenia' 'South Africa' 'Spain' 'Sri Lanka'
'Tajikistan' 'Thailand' 'Turkey' 'Turkmenistan' 'Ukraine' 'Vietnam']
Cluster 1: ['Afghanistan' 'Bangladesh' 'Benin' 'Burkina Faso' 'Cambodia' 'Cameroon'
'Chad' 'Ethiopia' 'Gabon' 'Ghana' 'Guinea' 'Haiti' 'India' 'Iraq'
'Jordan' 'Kenya' 'Lebanon' 'Liberia' 'Madagascar' 'Malawi' 'Mali'
'Mauritania' 'Morocco' 'Myanmar' 'Nepal' 'Niger' 'Nigeria' 'Pakistan'
'Rwanda' 'Senegal' 'Sierra Leone' 'Tanzania' 'Togo' 'Tunisia' 'Uganda'
'Zambia' 'Zimbabwe']
Cluster 2: ['Australia' 'Austria' 'Bahrain' 'Canada' 'Denmark' 'Estonia' 'Finland'
'France' 'Germany' 'Iceland' 'Ireland' 'Luxembourg' 'Netherlands'
'New Zealand' 'Norway' 'Singapore' 'Sweden' 'Switzerland'
'United Arab Emirates' 'United Kingdom' 'United States' 'Uruguay'
'Uzbekistan']
'''
多少个聚类?选择聚类的数量是成功进行K-Means聚类分析的最具挑战性的部分。该算法本身并不包含找出数据中多少个有意义的聚类。
当数据的维度增加时,寻找数据中的有意义的集群数量是一项困难的任务。
虽然没有一个完美的解决方案来寻找数据集中有意义的集群数量,但你可以采用一些不同的方法。在本书中,我们将不涉及聚类分析的这个方面,因为我们对聚类分析的了解足以进行有效的数据预处理。
8.2.3 中心点分析
中心点分析,实质上是一项典型的数据分析任务,一旦发现有意义的聚类就会进行。我们进行中心点分析,以了解每个聚类的形成原因,并深入了解数据中导致聚类形成的模式。
这种分析基本上是找到每个集群的中心点,并将它们相互比较。一个彩色编码的表格或热图对于比较中心点非常有用。下面的代码使用一个循环和布尔掩码找到中心点,然后使用seaborn模块中的sns.heatmap()函数来绘制彩色编码表。下面的代码必须在你运行了前面的代码片断后才能运行。
import seaborn as sns
clusters = ['Cluster {}'.format(i) for i in range(3)]
Centroids = pd.DataFrame(0.0,index=clusters,columns=Xs.columns)
for i,clst in enumerate(clusters):
BM = kmeans.labels_ == i
Centroids.loc[clst] = Xs[BM].median(axis=0)
sns.heatmap(Centroids,linewidths=.5,annot=True,cmap='binary')
plt.show()
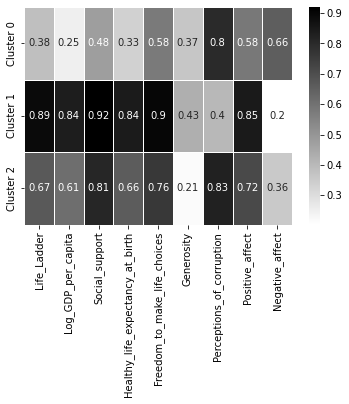
在我们分析前面的热图之前,请允许我给你提个醒。由于K-Means是一种基于随机的算法,你的输出可能与这里打印的输出不同。我们期望看到数据中出现相同的模式,但集群名称可能不同。
在前面的热图中,我们可以看到群组1在所有群组中拥有最好的幸福分数,所以我们可以把这个群组标记为非常幸福。另一方面,群组2在每项指标中都是第二好的,除了慷慨和对腐败的看法,所以我们将给这个群组贴上幸福但犯罪猖獗的标签。最后,群组0在几乎所有的幸福指数中都是最低的,但 "慷慨 "在所有中心点中排名第二;我们将把这个群组称为 "不幸福但慷慨"。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号