A*算法解决15数码问题_Python实现

1问题描述

数码问题常被用来演示如何在状态空间中生成动作序列。一个典型的例子是15数码问题，它是由放在一个4×4的16宫格棋盘中的15个数码(1-15)构成，棋盘中的一个单元是空的，它的邻接单元中的数码可以移到该单元中，通过这样不断地移动数码来改变棋盘布局，使棋盘从给定的初始棋局变为目标棋局(图1)。【数字华容道】

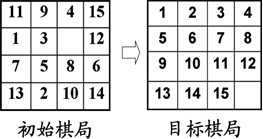
图1-1. 十五数码问题

2.知识表达

    常见的知识表达有状态空间、与/或图、语义网、谓词逻辑等。状态空间是表示问题及其搜索过程的一种方法，是人工智能最基本的形式化方法。对于数码问题，使用状态空间来描述更为直观易懂，更有助于对算法的理解，故本文采用状态空间来对问题进行表达。

    状态空间的三要素：状态、操作符、状态空间。

(1).状态S：十五数码问题中，每种棋局就是一个状态，所有棋局就是状态集合S，其中共有16！=209227898888000个状态。

(2).操作符F：使用最简化4个操作：分别向上、下、左、右移动空白单元，将操作符作用到某一状态即可从该状态转移到另一状态。但值得注意的是，并不是所有状态都可以执行这4个操作符。F = {上， 下， 左， 右}

(3).状态空间(S, F, G)，其中状态空间图G的一部分如图1-2所示。

图1-2. 十五数码的部分状态空间图

2. A*算法

2.1算法简介

A*算法是BFS的一个变种，不同于BFS的是，每次选择节点进行生成的时候，优先选择估价函数最小的节点，把原来的BFS算法的无启发式的搜索改成了启发式的搜索，可以有效的减少节点的搜索个数。其估价函数f(x)= g(x)+h(x)的设计对搜索效率的影响是至关重要的，对于十五数码问题的估价函数中的g(x)我们选择从初始状态到当前状态x的操作符个数，即搜索树中x状态的深度。对于启发函数h(x)，本文使用了两种方案：

(1).状态x中“不在位”的数码的个数，即当前状态x与目标状态不同元素的个数；

(2).曼哈顿距离，即当前状态x与目标状态不同元素之间对应横纵坐标差的绝对值之和。

2.2 算法原理

从初始状态S_0出发，分别采用不同的操作符作用于生成新的状态x并将其加入open表中（对应到状态空间图中便是根节点生成新的子节点n） ,接着从open表中按照某种限制或策略选择一个状态x使操作符作用于x又生成了新的状态并加入open表中(状态空间图中相应也产生了新的子节点)，如此不断重复直到生成目标状态。

对于以上所述的“某种策略”，在图搜索过程中，若该策略是依据进行排序并选取最小的估价值，则称该过程为A算法。其中:

 是从初始状态S_0经由状态x到目标状态S_G的代价估计

 是在状态空间中从初始状S_0态到状态x的实际代价

 是从状态x到目标状态S_G的最佳路径的代价

A算法中，若对所有的x存在h(x)≤,则称h(x)为的下限，表示某种偏于保守的估计。采用的下限h(x)为启发函数的A算法，称为A*算法，其中限制：h(x)≤h*(x)十分重要，它能保证A*算法找到最优解。在本问题中，g(x)相对容易得到，就是从初始节点到当前节点的路径代价，即当前节点在搜索树中的深度。关键在于启发函数h(x)的选择，A*算法的搜索效率很大程度上取决于估价函数h(x)。一般而言，满足h(x)≤h*(x)前提下，h(x)的值越大越好，说明其携带的启发性信息越多，A*算法搜索时扩展的节点就越少，搜索效率就越高。

传统的BFS是选取当前节点在搜索树中的深度作为g(x)，但没有使用启发函数h(x)，在找到目标状态之前盲目搜索，生成了过多的节点，因此搜索效率相对较低。本文分别使用不在位的元素个数和曼哈顿距离作为启发函数h(x)。每次从open表中选取时，优先选取估价函数最小的状态来扩展。

2.3 算法流程

本算法只考虑找到一条最优解即可，不需要找到所有可行解。

初始化两个表为空：open表和close表

1). 将初始节点加入open表(其父节点指针为null)

2). 若open表为空，则问题无解，退出。

3). 在open表中取出f(x)最小的节点作为当前节点x，并放入close表中；

4). 判断节点x是否为目标节点：若是，则找到问题的解，退出。

5). 若节点x不可扩展，则转到第2)步；

6). 扩展节点x(分别按照上、下、左、右方向移动空格并且操作起作用)得到多个子节点，计算它们的估价值并配置其父节点指针指向x，挨个判断每个子节点是否已经在open表中：

如果open表已有该子节点，比较二者的估价函数f(x)值，如果先前的f(x)大于现在新生成的子节点，则更新其为新生成的子节点，否则放弃加入，考察下一个子节点；（事实上，它们的h(x)是相同的，先出现的节点其g(x)不会大于后生成的，所以此步是没有必要的）

如果open表中没有该子节点且close表中也没有，则将该子节点加入open表中。

转到第2)步（对于open表没有该子节点但close表中有的情况不予处理，因为如果close表中节点的f(x)小于现在新生成的子节点，那么前者的子节点的估价函数也会小于后者子节点的估价函数，相应地也先被扩展，最终也会最先找到最优解，因为本文的目标是找到一条最佳路径即可）。

【一个思考：open表是不是可以考虑用set而不是用list，因为对于先加入open set的节点，其f(x)必然不会大于后加入的节点，所以后生成的节点在加入open set的时候，直接被拒绝就可以了】

【不清楚对不对，可以先看下这篇文章】