2017四川省赛D题《Dynamic Graph》
题意:给出一个n个点m条边的有向无环图(DAG),初始的时候所有的点都为白色。然后有Q次操作,每次操作要把一个点的颜色改变,白色<->黑色,对于每次操作,输出满足下列点对<u,v>,u,v都为白色且可以相互到达的个数。
数据范围:
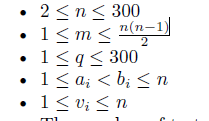
DAG上的问题,首先最暴力的方法就是,对于每一次更改都进行一遍dfs,B[u][v],表示U点可以到达v点,然后对于U的父亲结点来说,暴力合并,复杂度约为n^4,这样显然会爆炸。解法是每次用BITSET优化,因为B[u][v]的状态非零即一。
代码如下:
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int maxn = 350;
int N, M, Q;
struct Edge
{
int to, next;
Edge(int to = 0, int next = 0): to(to), next(next) {}
} E[maxn * maxn];
int head[maxn], tot;
void initedge()
{
memset(head, -1, sizeof(head));
tot = 0;
}
void addedge(int u, int v)
{
E[tot] = Edge(v, head[u]);
head[u] = tot++;
}
bitset<maxn>BT[maxn];
int vis[maxn], cul[maxn];
void init()
{
for(int i = 0; i <= N; i++)
{
BT[i].reset();
vis[i] = cul[i] = 0;
}
}
void DFS(int u)
{
BT[u].reset();
BT[u][u] = 1;
vis[u] = 1;
if(cul[u]) return ;
for(int k = head[u]; ~k; k = E[k].next)
{
int v = E[k].to;
if(!vis[v]) DFS(v);
if(!cul[v]) BT[u] |= BT[v];
}
}
int main ()
{
while(~scanf("%d %d %d", &N, &M, &Q))
{
init();
initedge();
for(int i = 1; i <= M; i++)
{
int u, v;
scanf("%d %d", &u, &v);
addedge(u, v);
}
for(int i = 1; i <= Q; i++)
{
int u, ans = 0;
scanf("%d", &u);
cul[u] ^= 1;
for(int i = 1; i <= N; i++) vis[i] = 0;
for(int i = 1; i <= N; i++)
{
if(!vis[i]) DFS(i);
ans += BT[i].count() - 1;
}
printf("%d\n", ans);
}
}
return 0;
}
另外还有一种方法:
维护F[u][v],表示u->v的路径条数,然后对于每次操作更新F[u][v]-+=F[u][x]*F[x][v],然后判断F[u][v]是否>0即可,这样做是对的,但是F[u][v]可能非常大,要用unsigned long long ,虽然unsigned long long 存不下,但是他有自动取模的功能,即使是这样也有可能出现F[u][v]之间有路径,但是取模后为0的情况,但是这个概率是很小的,unsigned long long 已经很大了,取模后出现零的情况应该不会被卡。unsigned int 也可以过。
代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long LL;
const int maxn = 350;
LL dp[maxn][maxn], vis[maxn];
int N, M, Q;
void init()
{
for(int i = 1; i <= N; i++)
{
vis[i] = 0;
for(int j = 1; j <= N; j++)
dp[i][j] = 0;
}
}
int main ()
{
while(~scanf("%d %d %d", &N, &M, &Q))
{
init();
for(int i = 1; i <= M; i++)
{
int u, v;
scanf("%d %d", &u, &v);
dp[u][v]++;
}
for(int k = 1; k <= N; k++ )
for(int st = 1; st < k; st++)
for(int ed = k + 1; ed <= N; ed++)
dp[st][ed] += dp[st][k] * dp[k][ed];
for(int i = 1; i <= Q; i++)
{
int u;
scanf("%d", &u);
if(vis[u] == 0)
{
vis[u] = 1;
for(int st = 1; st < u; st++)
for(int ed = u + 1; ed <= N; ed++)
dp[st][ed] -= dp[st][u] * dp[u][ed];
}
else
{
vis[u] = 0;
for(int st = 1; st < u; st++)
for(int ed = u + 1; ed <= N; ed++)
dp[st][ed] += dp[st][u] * dp[u][ed];
}
int ans = 0;
for(int st = 1; st <= N; st++)
{
if(vis[st]) continue;
for(int ed = st + 1; ed <= N; ed++)
{
if(vis[ed]) continue;
if(dp[st][ed] > 0) ans++;
}
}
printf("%d\n", ans);
}
}
return 0;
}
想的太多,做的太少。



