HDU 6154 + 找规律

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6154

题目描述：

　　在一个无限大小的二维正方形网格中，每次可以沿着网格的边长或者对角线画一条线，问题是：给出画出的封闭图形的面积为N，求需要最少的笔画数？

题解：

　　沿着对角线画出的图形的面积要比沿着边画出的图形的面积大，所以贪心的沿着对角线画。由于N的大小为（=<1e9）,所以笔画的个数不超过1e6,所以维护

dp[i] : 表示，当画i次，所能围城的最大的面积。分为一下四种情况：

1、i % 4 == 0,即可以组成正方形：

　　dp[i] = (i/4) * (i/4) * 2;

2、i % 4 == 1,即在组成的长方形的基础上多了一条边，则增加的面积为：

　　L = i /4;

　　dp[i] = dp[i-1] + (L + L -1)/2;(保留整数即可，输入的面积都是整数)

 

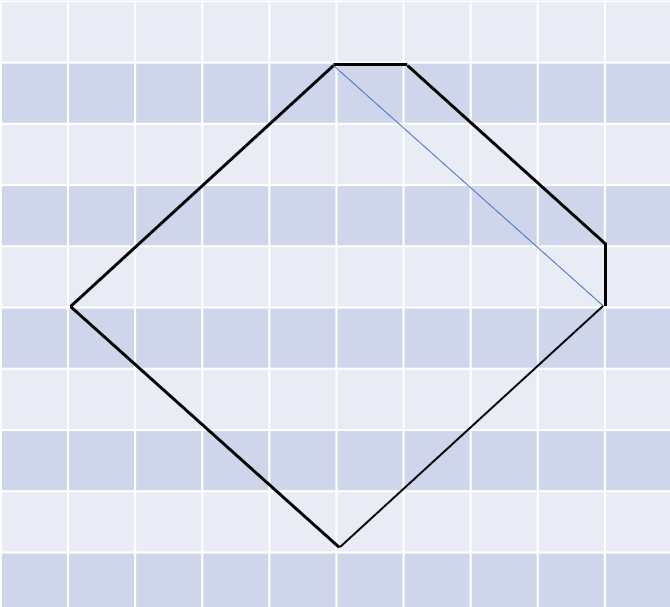
3、i % 4 == 2 时，在正方的基础，将任意对边的长度增加1，面积为：

　　L = i /4；

　　R = i/4 + 1;

　　dp[i] = L * R * 2；

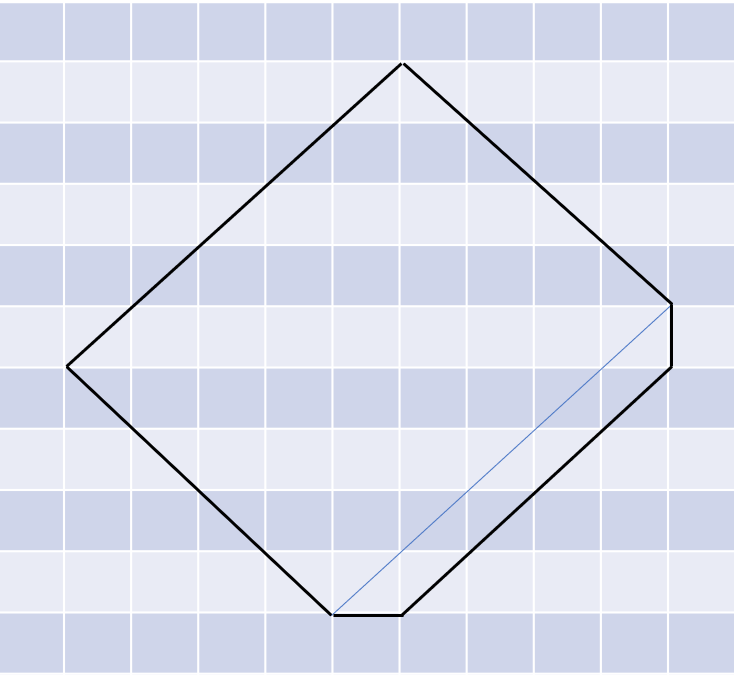
4、i % 4 == 3时，相当于在情况三组成的长方形基础上，增加一条边。所以我们将长方形的长边向外扩展，增加的面积为：

　　L = i /4；

　　R = i /4 + 1；

　　dp[i] = dp[i-1]  + (R + R -1) / 2;(同样的保留整数即可)

 

 

 代码输入：

#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int maxn = 1e6 + 15;
LL dp[maxn];
int Init()
{
    LL flag = 1e9 + 15;
    dp[1] = dp[2] = dp[3] = 0;
    dp[4] = 2, dp[5] = 2, dp[6] = 4;
    dp[7] = 5, dp[8] = 8;
    LL L, R;
    for (int i = 9;; i++)
    {
        if (i % 4 == 1)
        {
            L =  R =  i / 4;
            dp[i] = dp[i - 1] + (R + R - 1) / 2;
        }
        else if (i % 4 == 2)
        {
            L = i / 4;
            R = L + 1;
            dp[i] = L * R * 2;
        }
        else if(i % 4 == 3)
        {
            L =  i / 4;
            R =  L + 1;
            dp[i] = dp[i - 1] + (R + R - 1) / 2;
        }
        else
        {
            L = R = i / 4;
            dp[i] = L * R * 2;
        }
        if (dp[i] >= flag)
            return i;
    }
}
int main()
{
    int T, N;
    scanf("%d", &T);
    int pos = Init();
    while (T--)
    {
        scanf("%d", &N);
        int ans = lower_bound(dp + 1, dp + pos, (LL)N) - dp;
        printf("%d\n", ans);
    }
    return 0;
}