【组合数】Codeforces-869C. The Intriguing Obsession

题目链接(https://codeforces.com/problemset/problem/869/C)
C. The Intriguing Obsession

time limit per test 1 second

memory limit per test 256 megabytes

input standard input

output standard output

— This is not playing but duty as allies of justice, Nii-chan!

— Not allies but justice itself, Onii-chan!

With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they've never reached — water-surrounded islands!

There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist of \(a\), \(b\) and \(c\)distinct islands respectively.

Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length \(1\). For any two islands of the same colour, either they shouldn't be reached from each other through bridges, or the shortest distance between them is at least 3, apparently in order to prevent oddities from spreading quickly inside a cluster.

The Fire Sisters are ready for the unknown, but they'd also like to test your courage. And you're here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo \(998 244 353\). Two ways are considered different if a pair of islands exist, such that there's a bridge between them in one of them, but not in the other.

Input

The first and only line of input contains three space-separated integers \(a\), \(b\) and \(c\)$ (1 ≤ a, b, c ≤ 5 000)$ — the number of islands in the red, blue and purple clusters, respectively.

Output

Output one line containing an integer — the number of different ways to build bridges, modulo \(998 244 353\).

Examples

input

1 1 1

output

8

input

1 2 2

output

63

input

1 3 5

output

3264

input

6 2 9

output

813023575

Note

In the first example, there are \(3\) bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is \(2^3= 8\).

In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.

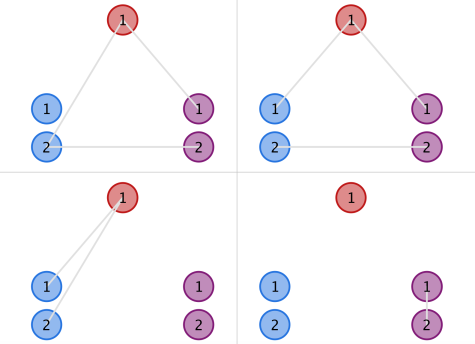
题意

岛上有三种颜色的岛屿，分别是红色、蓝色和紫色。岛群分别由 \(a\),\(b\)和\(c\)个不同的岛组成。

在一些（可能全部或没有）岛屿之间建立了桥梁。一座桥双向连接两个不同的岛，长度为\(1\)。对于任意两个相同颜色的岛，要么不能通过桥相互到达，要么它们之间的最短距离至少为 \(3\)。

Fire Sisters 已准备好迎接未知，但他们也想测试您的勇气。你来这里是为了找出在约束条件下建造所有桥梁的不同方法的数量，并给出模 \(998244353\) 的答案。如果存在一对岛，它们之间有一座桥，但另一种没有桥，则两种方法被认为是不同的。

思路

由题意可知，同岛不可建桥，如果一个岛中两个不同点连了另一个岛的同一个点也是不合法的。
根据抽屉原理,两岛中要想连边，两岛中选择的点的数量必须要相同。
然后从两岛中每次取\(i\)个点，取法共\(C(a,i)*C(b,i)\)。两岛分别找出来的\(i\)个点之间可以任意相连,共\(i!\)种。故\(ab\)两岛的合法答案有\(C(a,i)*C(b,i)*i!\)种。

同理三个岛的建桥操作，不进行不合法操作均可成立，易得三岛连线都是互不干扰的，可以分别计算，相乘取模即得答案。预处理可以用杨辉三角，也可以用阶乘的逆元。

（本题可以用dp写，我dp学的属实垃圾，想不来）

AC代码

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define llinf 0x3f3f3f3f3f3f3f3f
#define int long long
#define ull unsigned long long
#define PII pair<int,int>
using namespace std;
typedef long long ll;
const int N = 5e3 + 10;
const int mod = 998244353;
int a, b, c;
int C[N][N],fact[N];
inline int read() {//快读
	int f = 1, x = 0; char ch;
	do { ch = getchar(); if (ch == '-') f = -1; } while (ch<'0' || ch>'9');
	do { x = x * 10 + ch - '0'; ch = getchar(); } while (ch >= '0'&&ch <= '9');
	return x * f;
}
void init() {//阶乘，组合数预处理
	fact[0] = 1;
	for (int i = 0; i <= 5001; i++) {
		if (i) fact[i] = i * fact[i - 1] % mod;
		for (int j = 0; j <= i; j++) {
			if (!j) C[i][j] = 1;
			else C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
		}
	}
}
int fun(int x, int y) {//合法答案求法
	int res = 0;
	for (int i = 0; i <= min(x, y); i++) {
		res = (res + (C[x][i] * C[y][i] % mod * fact[i]) % mod) % mod;
	}
	return res;
}
void solve() {
	int ans1 = fun(a, b);
	int ans2 = fun(c, b);
	int ans3 = fun(a, c);
	int ans = ans1 * ans2 % mod * ans3 % mod;//相乘取模，输出
	printf("%lld\n", ans);
	return;
}
signed main() {
// 	ios::sync_with_stdio(false);
// 	cin.tie(0); cout.tie(0);
	a = read(); b = read(); c = read();
	init();
	solve();
	return 0;
}
/*
	i raised a cute kitty in my code,
	my friend who pass by can touch softly on her head:)

		 ／l、
   Meow~（ﾟ､ 。７
		 |、 ~ヽ
		 じしf_,)ノ

*/