【树形DP + 贪心】2020CCPC秦皇岛-K. Kingdom's Power
题目链接(https://codeforces.com/gym/102769/problem/K)
K. Kingdom's Power
time limit per test 2 seconds
memory limit per test 512 megabytes
input standard input
output standard output
Alex is a professional computer game player.
These days, Alex is playing a war strategy game. The kingdoms in the world form a rooted tree. Alex's kingdom \(1\) is the root of the tree. With his great diplomacy and leadership, his kingdom becomes the greatest empire in the world. Now, it's time to conquer the world!
Alex has almost infinite armies, and all of them are located at \(1\) initially. Every week, he can command one of his armies to move one step to an adjacent kingdom. If an army reaches a kingdom, that kingdom will be captured by Alex instantly.
Alex would like to capture all the kingdoms as soon as possible. Can you help him?
Input
The first line of the input gives the number of test cases, \(T (1≤T≤10^5)\). \(T\) test cases follow.
For each test case, the first line contains an integer \(n (1≤n≤10^6)\), where nn is the number of kingdoms in the world.
The next line contains \((n−1)\)integers \(f2,f3,⋯,fn (1≤fi<i)\), representing there is a road between \(fi\) and \(i\).
The sum of nn in all test cases doesn't exceed \(5×10^6\).
Output
For each test case, output one line containing "Case #x: y", where \(x\) is the test case number (starting from \(1\)), and \(y\) is the minimum time to conquer the world.
Example
input
2
3
1 1
6
1 2 3 4 4
output
Case #1: 2
Case #2: 6
题意
给出一个有$n $个节点的有根树,\(1\) 为根节点,根节点有无穷多个兵,每一秒可以让任意一个兵向任意一个地方移动一步,兵所到的点被占领,问最少需要经过多少秒,才能将所有的点都占领
思路
样例解释
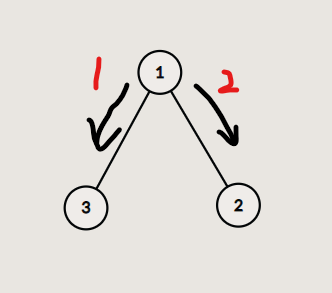
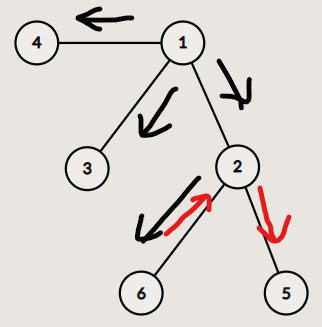
第一反应是dfs,但加上时间的限制,并且需要有贪心的操作,就需要做另外的处理。
如果所有的子节点都被占领,则经过的点都会被占领,那么问题转换为了到每个子节点的最短时间。
做法:用树形dp维护从根节点走更优还是从最近子结点更优,更新答案。维护一个变量表示到达当前节点的深度,递归返回最近的子节点过来的距离,维护距离与深度的最小值。
(特殊)假设只有一个士兵,对于每个子树而言,最长的链只走一次,其余的链都会走两次
因此,对于每个子树,按照 最长链 进行排序,因为最后只走一次其最长链
AC代码
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define llinf 0x3f3f3f3f3f3f3f3f
#define int long long
#define ull unsigned long long
#define PII pair<int,int>
using namespace std;
typedef long long ll;
const int N = 1e6 + 100;
const int mod = 1e9 + 7;
const double pi = acos(-1.0);
int t, n;
vector<PII>tree[N];//节点
int dep[N];//存深度
int cnt[N];//存距离
int res;
int dfs1(int u, int index)//index是当前点的深度
{
if (tree[u].empty()) return 1;//当前点没有子节点,贡献为1
dep[u] = index;//更新深度
for (auto &it : tree[u])
{
it.first = max(it.first, dfs1(it.second, index + 1));//更新最长链
}
sort(tree[u].begin(), tree[u].end());//按照最长链排序
return tree[u].back().first + 1;//有子节点,贡献 最深深度 + 1
}
int dfs2(int u, int index)//index是到达当前点的最短距离
{
cnt[u] = index;//更新距离
if (tree[u].empty()) return 1;//当前点没有子节点,贡献为1
int mi = index;//到当前节点的最近距离
for (auto it : tree[u])
{
mi = min(dep[u], dfs2(it.second, mi + 1));//维护距离与深度的最小值
}
return mi + 1;//有子节点,贡献 最短距离 + 1
}
void init() {//初始化
for (int i = 0; i <= n; i++) {
tree[i].clear();
}
res = 0;
return;
}
void solve() {
init();
cin >> n;
int x;
for (int i = 2; i <= n; i++) {//n - 1个节点
cin >> x;
tree[x].push_back({ 0,i });//初始存入子节点编号,深度未更新,初始0
}
//进行两次dfs维护最优解
dfs1(1, 0);
dfs2(1, 0);
for (int i = 1; i <= n; i++) {
if (tree[i].empty()) {//当前点没有子节点,即为最深点,更新答案
res += cnt[i];
}
}
return;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> t;
for (int i = 1; i <= t; i++) {
solve();
cout << "Case #" << i << ": " << res << endl;//输出
}
return 0;
}
/*
i raised a cute kitty in my code,
my friend who pass by can touch softly on her head:)
/l、
Meow~(゚、 。7
|、 ~ヽ
じしf_,)ノ
*/



