【并查集】2020CCPC秦皇岛-F. Friendly Group
题目链接(https://codeforces.com/gym/102769/problem/F)
F. Friendly Group
time limit per test 2.0 s
memory limit per test 512 megabytes
input standard input
output standard output
Professor Alex will organize students to attend an academic conference.
Alex has \(n\) excellent students, and he decides to select some of them (possibly none) to attend the conference. They form a group. Some pairs of them are friends.
The friendly value of the group is initially \(0\). For each couple of friends \((x,y)\), if both of them attend the conference, the friendly value of the group will increase \(1\), and if only one of them attends the conference, the friendly value of the group will decrease \(1\). If \(k\) students attend the conference, the friendly value of the group will decrease \(k\).
Alex wants to make the group more friendly. Please output the maximum friendly value of the group.
Input
The first line of the input gives the number of test cases, \(T (1≤T≤10^4)\). \(T\) test cases follow.
For each test case, the first line contains two integers \(n (1≤n≤3×10^5)\) and \(m (1≤m≤10^6)\), where \(n\) is the number of students and mm is the number of couples of friends.
Each of the following mm lines contains two integers \(xi,yi (1≤xi,yi≤n,xi≠yi)\), representing student$ xi$ and student \(yi\)are friends. It guaranteed that unordered pairs$ (xi,yi)$ are distinct.
The sum of \(n\) in all test cases doesn't exceed \(10^6\), and the sum of \(m\) in all test cases doesn't exceed \(2×10^6\).
Output
For each test case, output one line containing "Case #x: y", where \(x\) is the test case number (starting from \(1\)), and \(y\) is the maximum friendly value of the group.
Example
input
2
4 5
1 2
1 3
1 4
2 3
3 4
2 1
1 2
output
Case #1: 1
Case #2: 0
题意
给定\(n\)个学生,其中有\(m\)对好朋友\((x,y)\),老师要挑选一些学生去比赛,设定这群学生友谊值初始为0,
如果一对好朋友都被挑选到,群体友谊值\(+1\),如果一对好朋友当中只有其中一人被选中,群体友谊值\(-1\),如果有\(k\)个学生参加了比赛,群友谊值\(-k\),问挑选出学生群最大友谊值是多少。
思路
根据样例画图发现,\(答案数=通路数-人数\)
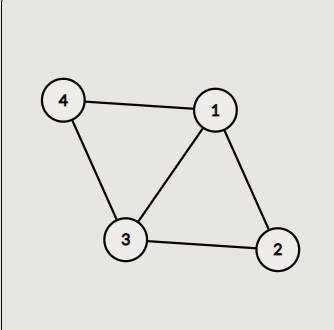
继续加边发现,单条的边对通路贡献为1,对人数t贡献也为1,所以单成链的边对答案没有贡献,只有单独的环路贡献为正
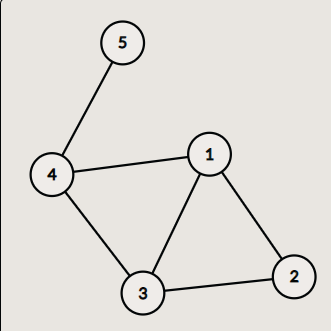
继续考虑,环套环,也是没有影响的
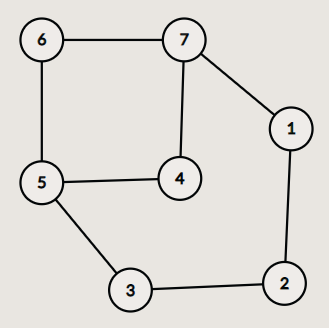
求集合最常用的算法为并查集,故以并查集模板
最后,差点以为是求友谊值最大的群,队友最后提出了群体不止一个(不好好读题的锅),所以把每个环路的正贡献相加即可
AC代码
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define llinf 0x3f3f3f3f3f3f3f3f
#define int long long
#define ull unsigned long long
#define PII pair<int,int>
using namespace std;
typedef long long LL;
const int N = 3e5 + 100;
const int mod = 1e9 + 7;
const double pi = acos(-1.0);
int t, n, m;
int root[N];
int road[N];//同一集合通路数
int cnt[N];//同一集合人数
int ans;
void init() {//初始化
for (int i = 0; i <= n; i++) {
root[i] = i;//初始以自己为根
road[i] = 0;//初始没通路
cnt[i] = 1;//初始只有自己一个人
}
return;
}
int find(int x) { return x == root[x] ? x : root[x] = find(root[x]); }//路径压缩
void merge(int x, int y) {
int dx = find(x);
int dy = find(y);
if (dx != dy) {//不同根
cnt[dx] += cnt[dy];//集合人数叠加
road[dx] += road[dy];//集合通路数叠加
//并根在增加操作之后
root[dy] = dx;
road[dx] ++;//并根时增加的一条通路
}
else {//同根,只有通路数增加
road[dx] ++;
}
return;
}
void solve() {
init();
int x, y;
while (m--) {//加边操作
cin >> x >> y;
if (y < x) swap(x, y);//这里我默认前面比后面的序号大,不知道对merge有没有影响
merge(x, y);
}
ans = 0;
for (int i = 1; i <= n; i++) {
if (root[i] == i) {
int t = road[i] - cnt[i];
if (t >= 0) ans += t;//如果贡献为正就相加
}
}
return;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> t;
for (int i = 1; i <= t; i++) {
cin >> n >> m;
solve();
cout << "Case #" << i << ": " << ans << endl;//输出
}
return 0;
}
/*
i raised a cute kitty in my code,
my friend who pass by can touch softly on her head:)
/l、
Meow~(゚、 。7
|、 ~ヽ
じしf_,)ノ
*/



