Baire Category Theorem
Theorem (Baire) Let $X$ be a complete metric space and $\{O_k\}_{k \geq 1}$ a countable collection of dense subsets of $X$. Then $\bigcap_{k=1}^{\infty} O_k$ is dense in $X$.
Analysis: This theorem belongs to the kind of propositions from which there seems to be no obvious tools or conditions for us to directly produce something as intermediate results or clues. Usually, such circumstances require an additional structure constructed by ourselves to assist the proof. Note that although the wording “constructed” is used here, it is not constructive proof. For this theorem, we need to construct a sequence of successively embedded balls, each of which is contained in a corresponding $O_k$ and any two balls from which are not tangent to each other. Meanwhile, the intersection of all these balls contains a point in any open set in $X$, which proves its density.
Proof: Let $U$ be an arbitrary open set in $X$. Because $O_1$ is dense in $X$, $O_1 \cap U$ is a nonempty open set. Select an $x$ from $O_1 \cap U$, there is an open ball $B_1 = B(x_1, r_1)$ contained in $O_1 \cap U$.
Similarly, because $O_2$ is dense, there is an $x_2$ in $O_2 \cap B_1$. Because $O_2 \cap B_1$ is open, there is another open ball $B_2 = B(x_2, r_2)$ embedded in $B_1$. We can select the radius $r_2$ of $B_2$ to be small enough such that the boundary of $B_2$ does not touch that of $B_1$, i.e. the two balls are not internally tangent. To determine a valid value range of $r_2$, two limiting cases should be considered.
- When $x_2$ is confined in the ball $B(x_1, \frac{r_1}{2})$, as long as $r_2$ is smaller than $\frac{r_1}{2}$, $B_2$ will not touch the boundary of $B_1$ (see Figure 1).
- When $x_2$ is selected outside the ball $B(x_1, \frac{r_1}{2})$, as long as $r_2$ is smaller than $r_1 - \rho(x_1, x_2)$, $B_2$ will not touch the boundary of $B_1$ (see Figure 2).
Therefore, by selecting $r_2 < \min\{\frac{r_1}{2}, r_1 - \rho(x_1, x_2)\}$, $B_2$ does not touch the boundary of $B_1$ so that $\bar{B}_2$ is completely contained within $B_1$.
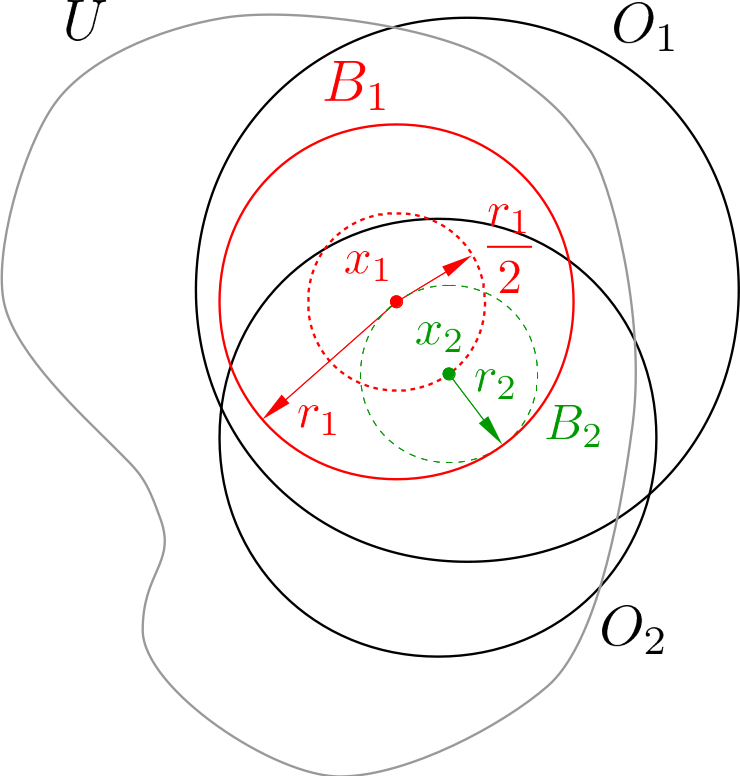
Figure 1. $B_2$ embedded in $B_1$ when $r_2 \approx \frac{r_1}{2}$.

Figure 2. $B_2$ embedded in $B_1$ when $r_2 \approx r_1 - \rho(x_1, x_2)$.
Continue the above operation, a sequence of open balls $\{B_k\}$ can be obtained such that $\bar{B}_{k+1} \subset B_k$, $B_k \subset O_k$ and $r_k \rightarrow 0$ when $k \rightarrow \infty$. For any $\varepsilon > 0$, there exists $N$ such that $r_N < \frac{\varepsilon}{2}$ and when $m, n > N$, $x_m$ and $x_n$, being the centers of $B_m$ and $B_n$ respectively, belong to the same ball $B_N$. Hence, $\rho(x_m, x_n) < 2r_N < \varepsilon$ and the sequence of ball centers $\{x_k\}$ is a Cauchy sequence. Because $X$ is complete, there exists $x$ in $X$ such that $x_k \rightarrow x$.
Because the sequence of balls are successively embedded, when $k > N$, $x_k$ belongs to $B_{N+1}$. In addition, because these ball are not internally tangent, the limit $x$ of $\{x_k\}$ is contained in $\bar{B}_{N+1}$, which is also contained in $B_N$ and then in $O_N$. Note that this $N$ is arbitrarily given, $x$ belongs to $\bigcap_{k=1}^{\infty} O_k$. Meanwhile, since any open ball $B_k$ is contained in the open set $U$, $x$ also belongs to $U$ and $U \cap \{\bigcap_{k=1}^{\infty} O_k\}$ is not empty. Because $U$ is arbitrary in $X$, $\bigcap_{k=1}^{\infty} O_k$ is dense.
$\square$
With Baire Theorem proved, Baire Category Theorem can be proved directly.
Theorem (Baire Category Theorem) Let $X$ be a complete metric space. Then no nonempty open subset of $X$ is of first category.
Proof: Let $\{E_n\}$ be a countable collection of nowhere dense sets and $O_n = (\bar{E}_n)^{\rm c}$, hence $O_n$ is dense. Due to Baire Theorem, $\bigcap_{n=1}^{\infty} O_n = \bigcap_{n=1}^{\infty} (\bar{E}_n)^{\rm c} = \left( \bigcup_{n=1}^{\infty} \bar{E}_n \right)^{\rm c}$ is dense in $X$. Therefore, any nonempty open set $U$ in $X$ has a nonempty intersection with it, which means $U$ is not contained in $\bigcup_{n=1}^{\infty} \bar{E}_n$ and neither is it contained in $\bigcup_{n=1}^{\infty} E_n$. So $U$ is not of first category. N.B. Because $X$ itself is a nonempty open set, $X$ is not of first category.
$\square$



