James Munkres Topology: Theorem 16.3
Theorem 16.3 If \(A\) is a subspace of \(X\) and \(B\) is a subspace of \(Y\), then the product topology on \(A \times B\) is the same as the topology \(A \times B\) inherits as a subspace of \(X \times Y\).
Comment: To prove the identity of two topologies, we can either show they mutually contain each other or prove the equivalence of their bases. Because a topological basis has smaller number of elements or cardinality than the corresponding topology, proof via basis is more efficient.
Proof: Let \(\mathcal{C}\) be the topological basis of \(X\) and \(\mathcal{D}\) be the basis of \(Y\). Because \(A \subset X\) and \(B \subset Y\), the subspace topological bases of them are \(\mathcal{B}_A = \{C \cap A \vert \forall C \in \mathcal{C} \}\) and \(\mathcal{B}_B = \{D \cap B \vert \forall D \in \mathcal{D} \}\) respectively according to Lemma 16.1.
Due to Lemma 15.1, the basis of the product topology on \(A \times B\) is
\[
\mathcal{B}_{A \times B} = \{ (C \cap A) \times (D \cap B) \vert \forall C \in \mathcal{C}, \forall D \in \mathcal{D} \}.
\]
Meanwhile, the basis of the product topology on \(X \times Y\) is
\[
\mathcal{B}_{X \times Y} = \{ C \times D \vert \forall C \in \mathcal{C}, \forall D \in \mathcal{D} \}.
\]
Restricting \(\mathcal{B}_{X \times Y}\) to the subset \(A \times B\), the basis of the subspace topology on \(A \times B\) is
\[
\begin{aligned}
\tilde{\mathcal{B}}_{A \times B} &= \{ (C \times D) \cap (A \times B) \vert \forall C \in \mathcal{C}, \forall D \in \mathcal{D} \} \\
&= \{ (C \cap A) \times (D \cap B) \vert \forall C \in \mathcal{C}, \forall D \in \mathcal{D} \},
\end{aligned}
\]
which is the same as that of the product topology on \(A \times B\). Hence, this theorem is proved.
The above process of proof can be illustrated as below.
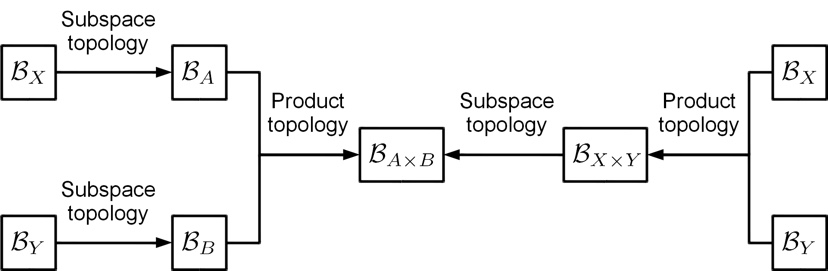
Remark: The above two routes for generating topology on \(A \times B\) must lead to the same result, otherwise, the theory itself is inappropriately proposed. A theory must be at least self-consistent before its debut in reality.



