AC 自动机学习笔记

前言

AC自动机（\(Aho\ Corasick\ Atomaton\)）有着一种 \(KMP\) 的思想，所以在学习之前建议先学一下 \(KMP\)。同时还需要了解一下 \(Trie\) 树（建议去看一下 oi-wiki 上的字典树）

问题描述

给定一个字符串 \(S\) 和 \(n\) 模式串，问有多少个模式串在 \(S\) 中出现过。

首先我们把 \(n\) 个模式串组成一个 \(Trie\)（就当你们学会了 \(Trie\) 树）

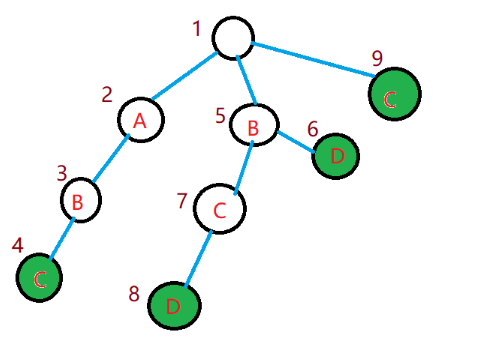
模式串：\(ABC,BCD,BD,C\)，其中绿色的点表示字符串的结尾。

对于 \(|S|=ABCBCD\)，那么我们在 \(Trie\) 上开始匹配，最开始会经过 \(2,3,4\) 三个点到 \(4\) 的时候，发现已经成功匹配了一个模式串了，那么现在我们需要从根在匹配一次吗？

显然的，不需要，\(KMP\) 的思想可以运用在这个 \(Trie\) 树上，我们在匹配完 \(4\) 的时候可以直接来到 \(7\) 然后再匹配到 \(8\)。

对于从 \(4\) 到 \(7\) 这个步骤，我们称 \(7\) 是 \(4\) 的 \(Fail\)（失配指针）。

\(Fail\) 指针

刚才说了 \(Fail\) 是失配指针，那么如果此时匹配失败，那么就到达这个指针指向的位置，所以，失配指针指向的节点是当前节点所代表的串，最长的、能与后缀匹配的，且在 \(Trie\)
中出现过的前缀所代表的节点。

我们设点 \(x\) 的父亲的 \(Fail\) 指针指向的是 \(p\)，那么如果 \(p\) 的儿子 \(y\) 和 \(x\) 相同，那么 \(x\) 的 \(Fail\) 指针指向的就是 \(y\)（应该挺好理解的吧）。

那么如果没有儿子呢？

那就再造一个儿子，就把当前节点的子节点指向当前节点的 \(fail\) 节点的子节点。

而且发现每个点 \(fail\) 指向的节点都比当前节点小，那么第二层的 \(fail\) 就指向根节点。

然后对于失配指针 \(Fail\) 我们需要使用 \(BFS\) 来实现。

inline void Get_fail(){
	for(int i=0;i<26;i++)
		if(ch[0][i])
			q.push(ch[0][i]),fail[ch[0][i]]=0;
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++)
			if(ch[u][i]) fail[ch[u][i]]=ch[fail[u]][i],q.push(ch[u][i]);
			else ch[u][i]=ch[fail[u]][i];//没有子节点，就把当前节点的子节点指向当前节点的fail节点的子节点
	}
}

查询

首先，指针指向根节点，依次读入单词，检查是否存在这个子节点。

然后指针跳转到子节点，如果不存在，直接跳转到失配指针即可。

inline int query(string s){
	int len=s.size(),v=0,res=0;
	for(int i=0;i<len;i++){
		v=ch[v][s[i]-'a'];
		for(int j=v;j&&val[j]>=0;j=fail[j]){
			res+=val[j];
			val[j]=-1;
		}
	}
	return res;
}

时间复杂度：\(O(|\Sigma|M)\)（\(| \Sigma |\) 一般来说是 \(26\)）。