SA后缀数组学习笔记
什么是后缀数组
后缀数组主要是用来处理字符串的，分为两种方法：倍增法以及 DC3，但由于倍增法通俗易懂，码量小，常数小，所以今天这篇文章我就只介绍倍增法（不可能是因为我不会 DC3）
前缀知识
No.1 基数排序
毕竟sort排序需要 \(O(nlog\ n)\)，所以并不适合后缀数组，我们便想到了 \(O(n)\) 的基数排序。
跟桶排序差不了多少，思想就是：将整数按位数切割成不同的数字，然后按每个位数分别比较。按每个位数从低位数到高位数分别比较。
然后在后缀数组中，我们就借用了这个思想来处理一个二元组，这之后我们还会接着讲。
No.2 文章中的数组介绍
\(sa_i\)：排名为i的后缀的位置
\(rak_i\)：从第i个位置开始的后缀的排名， \(rak_{sa_i}=i\)。
\(tp_i\)：基数排序的第二关键字，意义与sa一样
，即第二关键字排名为i的后缀的位置
\(tag_i\)：i号元素出现了多少次。辅助基数排序。
倍增法
我们上面不是提到了倍增吗，那么这个算法肯定需要 \(O(log_n)\) 完成排序。
如图所示，秉承着基数排序的思想，我们先弄出一个二元组，用两个长度为 \(1\) 的子串的排名 \(rak[i]\) 和 \(rak[i+1]\) 为第一关键字和第二关键字，进行一次基数排序，便让每个长度为 \(2\) 的子串 \(S_iS_{i+1}\) 得到了排名，得到了新的 \(sa\)。
然后在增加二元组中的两个子串的长度，但一个一个地增加太慢了，于是就运用倍增。继续进行排序：
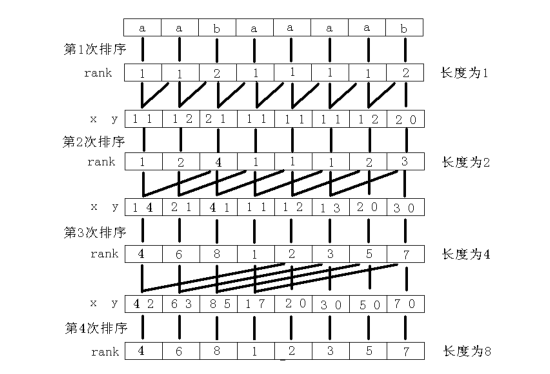
为什么倍增是正确的呢？
假如当前排序的长度为 \(2^{len}\)，那么因为 \(S_iS_{i+1}\dots S_{i+2^{len-1}}\) 和 \(S_{i+2^{len-1}+1} S_{i+2^{len-1}+2}\dots S_{i+2^{len}}\) 的排名我们在上一次排序已经得到，了，那么就可以把这两个子串的排名作为第一关键字和第二关键字进行基数排序就能得到新的排名了。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0,f=1;
char ch;
ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-f;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*f;
}
const int N=1114514;
char s[N];
int n,m=500,t;
int rak[N],tp[N],tag[N],sa[N];
inline void Radix_sort(){
for(int i=1;i<=m;++i) tag[i]=0;
for(int i=1;i<=n;++i)++tag[rak[i]];
for(int i=1;i<=m;++i) tag[i]+=tag[i-1];
for(int i=n;i>=1;--i) sa[tag[rak[tp[i]]]--]=tp[i],tp[i]=0;
}
inline void SA(){
int p=0;
for(int i=0;i<=m;++i) tag[i]=0;
for(int i=1;i<=n;++i) rak[i]=(int)s[i],tp[i]=i;
Radix_sort();
for(int k=1;k<=n;k<<=1){
p=0;
for(int i=0;i<=m;++i) tag[i]=tp[i]=0;
for(int i=n-k+1;i<=n;++i) tp[++p]=i;
for(int i=1;i<=n;++i)
if(sa[i]>k)
tp[++p]=sa[i]-k;
Radix_sort();
swap(rak,tp);
rak[sa[1]]=1;
p=1;
for(int i=2;i<=n;++i)
rak[sa[i]]=(tp[sa[i-1]]==tp[sa[i]]&&tp[sa[i-1]+k]==tp[sa[i]+k])?p:++p;
if(p>=n) break;
m=p;
}
}
signed main(){
scanf("%s",s+1);
n=strlen(s+1);
SA();
for(int i=1;i<=n;++i)
printf("%lld ",sa[i]);
return 0;
}
建议下一篇阅读 LCP与height数组
