fhq_treap 学习笔记

Treap 是一种二叉平衡树，而 Treap = BST + Heap。

但普通的 Treap 每次都要旋来旋去的，泰麻饭啦！于是出现了 fhq_treap，也就是无旋 treap。

fhq_treap 整体是拥有二叉搜索树的性质，但是它的每一个节点都会有一个附加权值，它的附加权值是符合堆的性质。附加权值需要随机，这样能让他尽量平衡，防止成一条链（当然也有可能成链，不过比出门被核弹创死的可能性还要低）。

首先要初始化：

初始化

首先定义个树。

struct node{
    int l,r,key,val,size;
	//l 左节点，r 右节点 ，key 他的权值，val 给他的附加权值，size 树的大小
}tree[N];

初始化树

int getrand(int x){
	tree[++cnt].key=x;//权值
	tree[cnt].val=rand();//附加权值
	tree[cnt].size=1;//子树大小
	return cnt;
}

push_up

就是和线段树一样，上传子树的大小，来求出当前树的大小。

void pushup(int p){
	tree[p].size=tree[tree[p].l].size+tree[tree[p].r].size+1;
}

treap 主要有两个操作 split 和 merge，也就是分裂与合并。

split

思想就是把一个treap分成两个，可以看一下图：

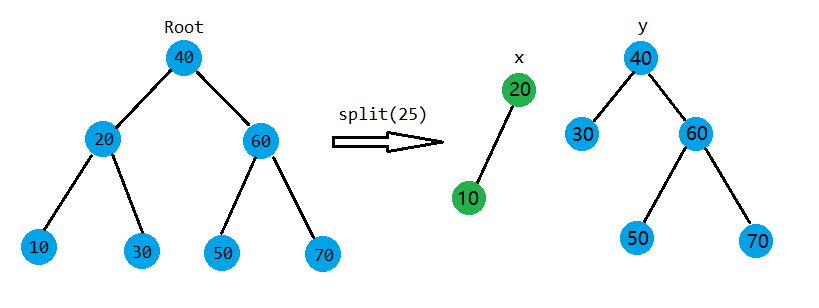
用两种方法：按值分裂、按大小分裂。

首先是按值分裂，

这个就是按照他的权值，因为满足二叉搜索树，所以只需要判断比当前节点大还是小，就可以知道要分得值是在在左边还是右边。

void split(int p,int x,int &l,int &r){//分裂 
	    if(!p){
	        l=r=0;
	        return ;
	    }
	    if(tree[p].key<=x){//判断权值是小还是大，根据权值去找比他小的。
	        l=p;
	        split(tree[l].r,x,tree[l].r,r);
	    }else{
	        r=p;
	        split(tree[r].l,x,l,tree[r].l);
	    }
	    pushup(p);//标记上传
	}

然后就是按大小分裂：

void split(int p,int x,int &l,int &r) {
	if(p==0){
		l=r=0;
		return;
	}
	if(tree[tree[p].l].size+1<=x){
		l=p;
		split(tree[p].r,x-tree[tree[p].l].x-1,tree[p].r,r);
	} 
	else{
		r=p;
		split(tree[p].l,x,l,tree[p].l);
	}
	pushup(p);
}

merge

将两棵平衡树合起来，同时满足其heap值的堆性质，返回合并后的根序号，保证以 \(a\) 为根的树种每个节点的权值都小于以 \(b\) 为根的每个节点的权值

当两棵子树其中有一棵为空时，将根设为 \(a+b\)（即非空树的根序号）

当 \(val_a<=val_b\) 时，
将当前根设为 \(a\)，同时合并 \(l_r\) 和 \(b\)。

否则，
将当前根设为 \(b\)，同时合并 \(a\) 和 \(r_l\)。


int merge(int l,int r){//合并 
	if(!l||!r)
	    return l+r;
	if(tree[l].val<=tree[r].val){
	    tree[l].r=merge(tree[l].r,r);
	    pushup(l);
	    return l;
	}else{
	    tree[r].l=merge(l,tree[r].l);
	    pushup(r);
	    return r;
	}
}

插入

就是现将树按照 \(x\) 的大小分为两棵树，直接将要插入的数插入左边的最后后的树，再与右边合并。

void insert(int x){//插入 
	split(rt,x-1,dl,dr);
	rt=merge(merge(dl,getrand(x)),dr);
}

删除

删除权值为 \(k\) 的点，先把整颗树以 \(k\) 为权值split成两棵树 \(l,r\),再把 \(l\) 树按照 \(k-1\) 分成 \(l,mid\)。这时候值为k的点一定为 \(mid\) 的根（应为 \(l\) 中都是小于等于 \(k\) 的数，而 \(mid\) 中都是大于 \(k-1\) 的数，那么 \(mid\) 里面一定是 \(k\)），那么我们把 \(mid\) 的两个子儿子merge起来，就是去除掉 \(k\)，再把他们重新merge起来得到一个新的树。

void delet(int x){//删除 
    split(rt,x-1,dl,dr);
    split(dr,x,tmp,dr);
    tmp=merge(tree[tmp].l,tree[tmp].r);
    rt=merge(dl,merge(tmp,dr));
}

例题

P3369 【模板】普通平衡树

一道版子题，但有些还要提两嘴。

查询 \(x\) 数的排名

直接按照 \(x-1\) 的权值把树分开，那么 \(l\) 树中最大的应该小于等于 \(x-1\)，那么k的排名就是 \(size_i+1\)。

int getrk(int x){//查询x的排名 
	    split(rt,x-1,dl,dr);
	    int rnk=tree[dl].size+1;
	    rt=merge(dl,dr);
	    return rnk;
	}

查询排名为 \(x\) 的数

就是可以直接遍历整个树，但由于只需要找排名为 \(x\) 的，又由于我们之前已经算过子树的大小，那么只需要判断排名为 \(x\) 的数在哪棵子树那就直接搜这棵子树。

前驱与后驱

前驱

你按照 \(x-1\) 掰开这棵树,就可以保证这棵树都是 \(\le x-1\) 的,然后找最大值。

后驱

按照 \(x\) 掰开这棵树,就可以保证这棵树都是 \(\ge k\) 的,然后找最小值。

P3369 【模板】普通平衡树代码

#include<bits/stdc++.h>
using namespace std;
const int N=200005;
inline int read()
{
	int f = 1, res = 0;
	char c = getchar();
	while (c < '0' || c > '9')
	{
		if (c == '-') f = -1;
		c = getchar();
	}
	while (c >= '0' && c <= '9')
	{
		res = (res << 3ll) + (res << 1ll) + c - '0';
		c = getchar();
	}
	return f * res;
}
int n,cnt,dl,dr,tmp,rt;
int opt,x;
struct node{
    int l,r,key,val,size;
}tree[N];
struct FHQ_Treep{
	int getrand(int x){
	    tree[++cnt].key=x;
	    tree[cnt].val=rand();
	    tree[cnt].size=1;
	    return cnt;
	}
	void pushup(int p){
	    tree[p].size=tree[tree[p].l].size+tree[tree[p].r].size+1;
	}
	void split(int p,int x,int &l,int &r){//分裂 
	    if(!p){
	        l=r=0;
	        return ;
	    }
	    if(tree[p].key<=x){
	        l=p;
	        split(tree[l].r,x,tree[l].r,r);
	    }else{
	        r=p;
	        split(tree[r].l,x,l,tree[r].l);
	    }
	    pushup(p);
	}
	int merge(int l,int r){//合并 
	    if(!l||!r)
	        return l+r;
	    if(tree[l].val<=tree[r].val){
	        tree[l].r=merge(tree[l].r,r);
	        pushup(l);
	        return l;
	    }else{
	        tree[r].l=merge(l,tree[r].l);
	        pushup(r);
	        return r;
	    }
	}
	void insert(int x){//插入 
	    split(rt,x-1,dl,dr);
	    rt=merge(merge(dl,getrand(x)),dr);
	}
	void delet(int x){//删除 
	    split(rt,x-1,dl,dr);
	    split(dr,x,tmp,dr);
	    tmp=merge(tree[tmp].l,tree[tmp].r);
	    rt=merge(dl,merge(tmp,dr));
	}
	int getrk(int x){//查询x的排名 
	    split(rt,x-1,dl,dr);
	    int rnk=tree[dl].size+1;
	    rt=merge(dl,dr);
	    return rnk;
	}
	int getnum(int p,int x){//前驱和后驱 
	    int u=tree[tree[p].l].size+1;
	    if(u==x) return tree[p].key;
	    if(u>x) return getnum(tree[p].l,x);
	    else return getnum(tree[p].r,x-u);
	}
}fhq_Treep;
int main(){
    n=read();
    for(int i=1;i<=n;++i){
        opt=read();x=read();
        if(opt==1) fhq_Treep.insert(x);
        else if(opt==2) fhq_Treep.delet(x);
        else if(opt==3) printf("%d\n",fhq_Treep.getrk(x));
        else if(opt==4) printf("%d\n",fhq_Treep.getnum(rt,x));
        else if(opt==5){
            fhq_Treep.split(rt,x-1,dl,dr);
            printf("%d\n",fhq_Treep.getnum(dl,tree[dl].size));
            rt=fhq_Treep.merge(dl,dr);
        }else{
            fhq_Treep.split(rt,x,dl,dr);
            printf("%d\n",fhq_Treep.getnum(dr,1));
            rt=fhq_Treep.merge(dl,dr);
        }
    }
    return 0;
}

P3391 【模板】文艺平衡树

这道题多了一个操作：

翻转

由于上文说过，分裂的时候可以按照大小来划分，那么只需要将比 \(l\) 小的分裂出来，再把比 \(r\) 大的分裂出来，那么剩下的不就是 \(l\) 到 \(r\) 了吗。

fhq_Treep.splitq(rt,y,dl,dr);
fhq_Treep.splitq(dl,x-1,dl,p);
tree[p].lazy^=1;
rt=fhq_Treep.mergeq(fhq_Treep.mergeq(dl,p),dr);

P3391 【模板】文艺平衡树代码

#include<bits/stdc++.h>
using namespace std;
const int N=500005;
inline int read()
{
	int f = 1, res = 0;
	char c = getchar();
	while (c < '0' || c > '9')
	{
		if (c == '-') f = -1;
		c = getchar();
	}
	while (c >= '0' && c <= '9')
	{
		res = (res << 3ll) + (res << 1ll) + c - '0';
		c = getchar();
	}
	return f * res;
}
int n,m,cnt,dl,dr,tmp,rt,p;
int y,x;
struct node{
    int l,r,val,key,size,lazy;
}tree[N];
struct FHQ_Treep{
	int getrand(int x){
	    tree[++cnt].val=x;
	    tree[cnt].key=rand();//防止成链 
	    tree[cnt].size=1;
	    tree[cnt].l=0;
	    tree[cnt].r=0;
	    return cnt;
	}
	void pushup(int p){
	    tree[p].size=tree[tree[p].l].size+tree[tree[p].r].size+1;
	}
	void pushdown(int u){//下传懒标记
		swap(tree[u].l,tree[u].r);
		tree[tree[u].l].lazy^=1;
		tree[tree[u].r].lazy^=1;
		tree[u].lazy=0;
	}
	void splitq(int p,int x,int &l,int &r){
		if(!p){
			l=r=0;
			return ;
		}
		if(tree[p].lazy)
			pushdown(p);
		if(tree[tree[p].l].size+1<=x){
			l=p;
			splitq(tree[p].r,x-tree[tree[p].l].size-1,tree[p].r,r);
		}
		else{
			r=p;
			splitq(tree[p].l,x,l,tree[p].l);
		}
		pushup(p);
	}
	int mergeq(int l,int r){//合并 
		if(!l||!r)
			return l+r;
		if(tree[l].key<tree[r].key){
			if(tree[l].lazy)
				pushdown(l);
			tree[l].r=mergeq(tree[l].r,r);
			pushup(l);
			return l;
		}
		else{
			if(tree[r].lazy)
				pushdown(r);
			tree[r].l=mergeq(l,tree[r].l);
			pushup(r);
			return r;
		}	
	}
	void print(int x){
		if(tree[x].lazy){
			pushdown(x);
		}
		if(tree[x].l)
			print(tree[x].l);
		printf("%d ",tree[x].val);
		if(tree[x].r)
			print(tree[x].r);
	}
}fhq_Treep;
int main(){
    n=read();m=read();
    for(int i=1;i<=n;++i)
    	rt=fhq_Treep.mergeq(rt,fhq_Treep.getrand(i));
    for(int i=1;i<=m;++i){
        x=read();y=read();
		fhq_Treep.splitq(rt,y,dl,dr);
	 	fhq_Treep.splitq(dl,x-1,dl,p);
		tree[p].lazy^=1;
		rt=fhq_Treep.mergeq(fhq_Treep.mergeq(dl,p),dr);
    }
    fhq_Treep.print(rt);
    return 0;
}

posted @ 2023-05-10 18:58 bhbjzyh 阅读(45) 评论(0) 编辑收藏举报

刷新页面返回顶部

pdpdzaa