python数据分析与挖掘实战第三章

第三章 数据探索

  数据探索就是通过检验数据集的数据质量、绘制图表、计算某些特征量等手段，对样本数据的结构和规律进行分析的过程。数据探索有助于选择合适的数据预处理和建模方法。数据探索包括数据质量分析和数据特征分析。

3.1 数据质量分析

  数据质量分析的主要任务是检查原始数据中是否存在脏数据。脏数据一般指不符合要求以及不能直接进行分析的数据，常见有：缺失值、异常值、不一致值、重复数据、含有特殊符号的数据。

3.1.1. 缺失值分析

  数据的缺失主要包括记录的缺失和记录中某个字段信息的缺失。两者都会造成分析结果不准确。产生原因主要有：某些信息暂时无法获取、信息被遗漏、属性值不存在。

  使用简单的统计分析，可以得到含有缺失值的属性的个数，以及每个属性的未缺失数、缺失数与缺失率。从总体上来说，缺失值的处理分为删除存在缺失值的记录、对可能值进行插补和不处理3种情况。

2. 异常值（离群点）分析

  异常值分析是检验数据是否有录入错误，是否含有不合常理的数据。异常值指样本中的个别值，其数值明显偏离其他的观测值。

• 简单统计量分析（描述性统计，进而查看哪些数据不合理，例如最大值和最小值）

• 3σ原则（3倍标准差）

• 箱型图分析（小于上四分位数-1.5四分位数间距或大于上四分位数+1.5四分位数间距）

代码清单3-1 使用describe()方法查看数据的基本情况

# 代码3-1
import pandas as pd
catering_sale= "D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/catering_sale.xls"  # 餐饮数据
data = pd.read_excel(catering_sale, index_col = u'日期')  # 读取数据，指定“日期”列为索引列
print(3107)
print(data)
print(data.describe(),data.describe().max()-data.describe().min())

代码清单3-1运行结果：

 

 

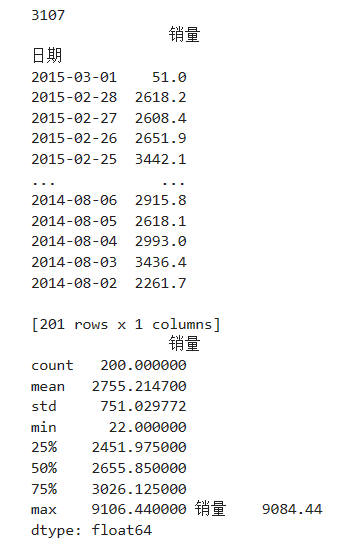
代码清单3-2 餐饮日销额数据异常值检测

# 代码3-2 餐饮销额数据异常值检测
import matplotlib.pyplot as plt  # 导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

plt.figure()  # 建立图像
p = data.boxplot(return_type='dict')  # 画箱线图，直接使用DataFrame的方法
x = p['fliers'][0].get_xdata()  #  'flies'即为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort()  # 从小到大排序，该方法直接改变原对象


for i in range(len(x)):
    if i>0:
        plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]),y[i]))
    else:
        plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.08,y[i]))

plt.title('异常值检测箱型图(3107)')
plt.show()  # 展示箱线图

代码清单3-2运行结果：

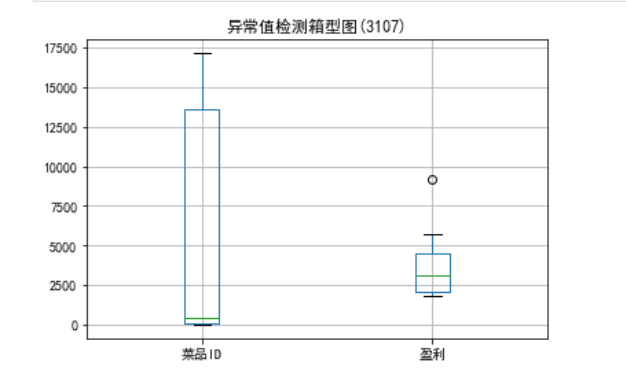
3. 不一致的值

  数据不一致性是指数据的矛盾性、不相容性。例如，两张表中都储存了用户的电话号码，但在用户的电话号码发生改变时只更新了一张表中的数据。

3.2 数据特征分析

  通过绘制图表、计算某些特征量进行数据的特征分析。

3.2.1.分布分析

分布分析能揭示数据的分布特征和分布类型。

1）定量数据：求极差->决定组距与组数->决定分点->列出频率分布表->绘制频率分布直方图。

代码清单3-3  "捞起生鱼片"的季度销售情况

# 代码3-3 "捞起生鱼片"的季度销售情况
import pandas as pd
import numpy as np
catering_sale = "D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/catering_fish_congee.xls"  # 餐饮数据
data = pd.read_excel(catering_sale,names=['date','sale'])  # 读取数据，指定“日期”列为索引
print(data.describe())

bins = [0,500,1000,1500,2000,2500,3000,3500,4000]
labels = ['A_lei','[500,1000)','[1000,1500)','[1500,2000)',
       '[2000,2500)','[2500,3000)','[3000,3500)','[3500,4000)'] 
data['sale分层'] = pd.cut(data.sale, bins, labels=labels)
print(data)
aggResult = data.groupby('sale分层').agg({'sale':'count'})
print(aggResult)
pAggResult = round(aggResult/aggResult.sum(), 2, )


import matplotlib.pyplot as plt
plt.figure(figsize=(9,7))  # 设置图框大小尺寸
pAggResult['sale'].plot(kind='bar',width=0.6,fontsize=10)  # 绘制频率直方图
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.title('季度销售额频率分布直方图_number001(3107)',fontsize=20)
plt.show()

代码清单3-3运行结果:

 

 

 

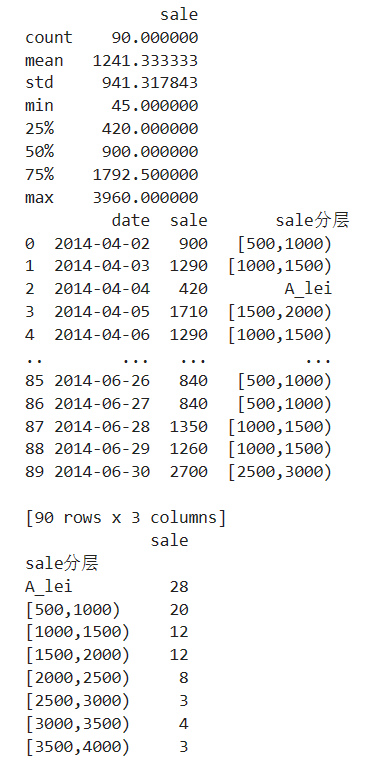
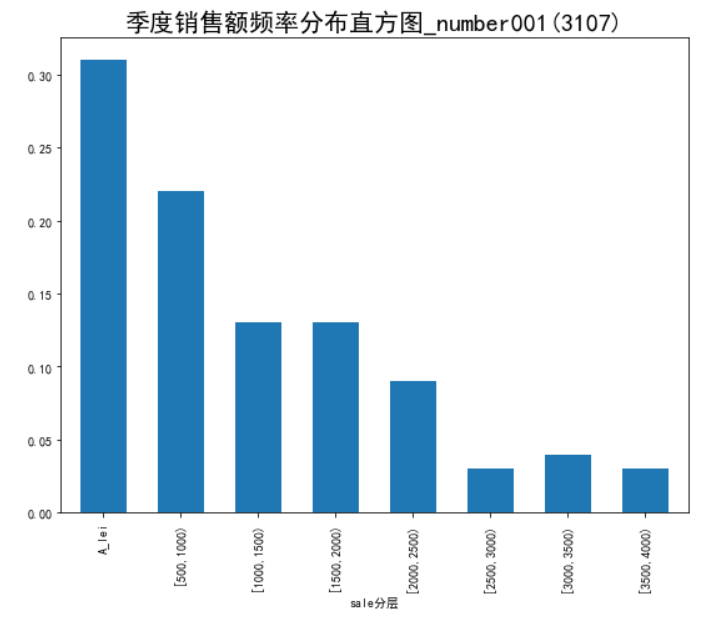
2）定性数据的分布分析：根据变量的分类类型来分组，采用饼图和条形图来描述

代码清单3-4 不同菜品在某段时间的销售量的分布情况

import pandas as pd
import matplotlib.pyplot as plt
catering_dish_profit = 'D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/catering_dish_profit.xls'  # 餐饮数据
data = pd.read_excel(catering_dish_profit)  # 读取数据，指定“日期”列为索引

#绘制饼图
x=data['盈利']
labels = data['菜品名']
plt.figure(figsize=(8,6))   #设置画布大小
plt.pie(x,labels=labels)   #绘制饼图
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.title('菜品销售量分布（饼图）3107')
plt.axis('equal')
plt.show()

#绘制条形图
x = data['菜品名']
y = data['盈利']
plt.figure(figsize=(8,4))   #设置画布大小
plt.bar(x,y)
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.xlabel('菜品')
plt.ylabel('销量')
plt.title('菜品销售量分布（条形图）3107')
plt.show()

代码清单3-4运行结果:

3.2.2.对比分析

  对比分析是指把两个相互联系的指标进行比较，从数量上展示和说明研究对象规模的大小，水平的高低，速度的快慢，以及各种关系是否协调。

 

2.1绝对数比较

2.2相对数比较：结构、比例、比较、强度、计划完成程度、动态

# 代码3-5
# 绘制不同部门的各月份销售额对比情况
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_excel("D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/dish_sale.xls")
plt.figure(figsize=(8,4))
plt.plot(data['月份'], data['A部门'], color='green', label='A部门', marker='o')
plt.plot(data['月份'], data['B部门'], color='red', label='B部门', marker='s')
plt.plot(data['月份'], data['C部门'], color='skyblue', label='C部门', marker='x')
plt.legend()  # 显示图例
plt.title('3部门之间销售额比较（3107）')
plt.ylabel('销售额（万元）')
plt.xlabel('月份')
plt.show()

# 绘制B部门各年份各月份的销售额折线图
data = pd.read_excel('D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/dish_sale_b.xls')
plt.figure(figsize=(8, 4))
plt.plot(data['月份'], data['2012年'], color='green', label='2012年', marker='o')
plt.plot(data['月份'], data['2013年'], color='red', label='2013年', marker='s')
plt.plot(data['月份'], data['2014年'], color='skyblue', label='2014年', marker='x')
plt.legend()  # 显示图例
plt.title('B部门各年份销售额比较（3107）')
plt.ylabel('销售额（万元）')
plt.xlabel('月份')
plt.show()

3.2.3. 统计量分析

 

1）集中趋势度量：均值、中位数、众数

2）离中趋势：极差、标准差（方差）、变异系数、四分位间距

#代码3-6 餐饮销量数据统计量分析
import pandas as pd
catering_sale= "D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/catering_sale.xls"  # 餐饮数据
data = pd.read_excel(catering_sale, index_col = u'日期')  # 读取数据，指定“日期”列为索引列

data = data[(data['销量']>400) & (data['销量']<5000)]
statistics = data.describe()

statistics.loc['range'] = statistics.loc['max'] - statistics.loc['min']  # 极差
statistics.loc['var'] = statistics.loc['std'] / statistics.loc['mean']  # 变异系数
statistics.loc['dis'] = statistics.loc['75%'] - statistics.loc['25%']  # 四分位数间距
print('餐饮销量数据统计量分析（3107）')
print(statistics)

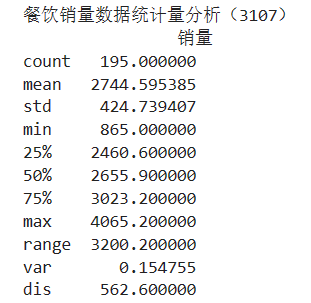
3.2.4. 周期性分析

  周期性分析是探索某个变量是否随着时间变化而呈现出某种周期变化趋势。

 

# 代码3-7
import pandas as pd
import matplotlib.pyplot as plt

df_normal = pd.read_csv("D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/user.csv")
plt.figure(figsize=(8, 4))
plt.plot(df_normal['Date'], df_normal['Eletricity'])
plt.xlabel('日期')
x_major_locator = plt.MultipleLocator(7)  # 设置x轴刻度间隔
ax = plt.gca()
ax.xaxis.set_major_locator(x_major_locator)
plt.ylabel('每日电量')
plt.title('正常用户电量趋势(3107)')
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用于正常显示中文标签
# plt.axis('equal')
plt.show()  # 展示图片

# 窃电用户用电趋势分析
df_steal=pd.read_csv("D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/Steal user.csv")
plt.figure(figsize = (10,9))
plt.plot(df_steal["Date"],df_steal["Eletricity"])
plt.xlabel("日期")
plt.ylabel("日期")
x_major_locator = plt.MultipleLocator(7)  # 设置x轴刻度间隔
ax = plt.gca()
ax.xaxis.set_major_locator(x_major_locator)
plt.title("窃电用户电量趋势(3107)")
plt.rcParams['font.sans-serif']=['SimHei']
plt.show()

 

 

 

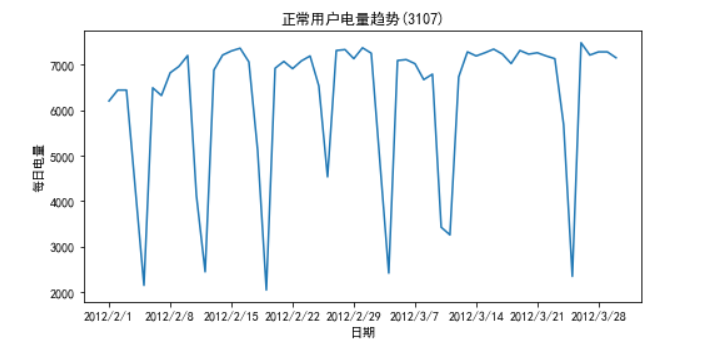
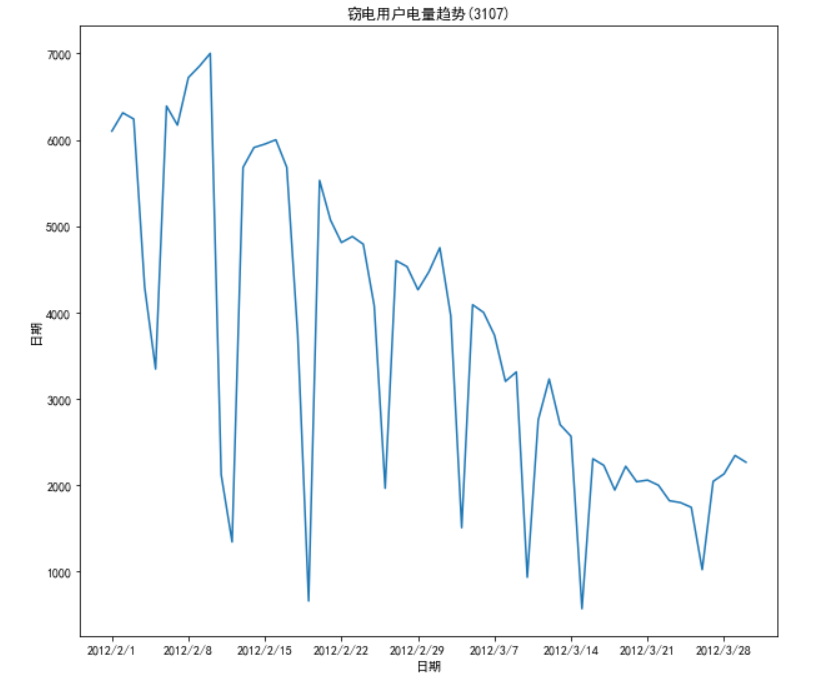
3.2.5.贡献度分析

  贡献度分析又称帕累托分析，它的原理是帕累托法则，又称20/80定律。同样的投入放在不同的地方会产生不同的效益。例如，对一个公司来讲，80%的利润常常来自于20%最畅销的产品，而其他80%的产品只产生了20%的利润。

 

# 代码3-8
import pandas as pd
# 初始化数据参数
dish_profit = 'D:/Computer Class/Jupyter/JupyterLab-Portable-3.1.0-3.9/notebooks/python/catering_dish_profit.xls'
data = pd.read_excel(dish_profit, index_col='菜品名')
data = data['盈利'].copy()
data.sort_values(ascending=False)  # 排序

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用于正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用于正常显示负号

plt.figure()
data.plot(kind='bar')
plt.ylabel('盈利（元）')
p = 1.0 * data.cumsum() / data.sum()  # 分别计算总盈利额占该盈利额的值
p.plot(color='r', secondary_y=True, style='-o', linewidth=2)
# 添加注释，即85%处的标记。这里包括了指定箭头样式。
plt.annotate(format(p[6], '.4%'), xy=(6, p[6]), xytext=(6 * 0.9, p[6] * 0.9), 
             arrowprops=dict(arrowstyle='->', connectionstyle='arc3, rad=.2'))
plt.ylabel('盈利（比例）')
plt.title('菜品盈利数据帕累托图（3107）')
plt.show()

 

 

 

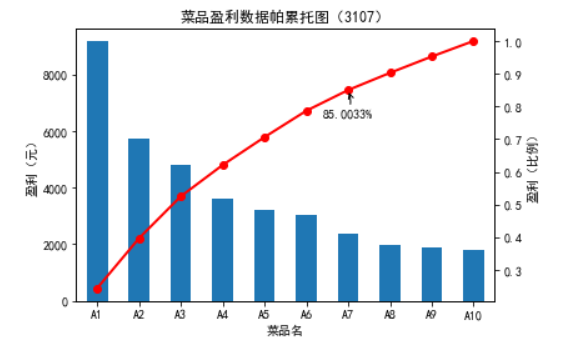
6.相关性分析

分析连续变量之间线性相关程度的强弱。

 

#代码3-9
import pandas as pd
catering_sale ='catering_sale_all.xls'
data = pd.read_excel(catering_sale, index_col='日期')

print(data.corr())  # 相关系数矩阵，即给出了任意两款菜式之间的相关系数
print(data.corr()['百合酱蒸凤爪'])  # 只显示“百合酱蒸凤爪”与其他菜式的相关系数
print(data['百合酱蒸凤爪'].corr(data['翡翠蒸香茜饺']))  #计算“百合酱蒸凤爪”与“翡翠蒸香茜饺”的相关系数

 

 

 

3.3 python主要数据搜索函数

  python中用于数据探索的库主要是pandas（数据分析）和Matplotlib（数据可视化）。pandas提供了大量与数据探索相关的函数，可大致分为统计特征函数与统计绘图函数，而绘图函数依赖于Matplotlib，所以会跟Matplotlib结合使用。

 

 

3.3.1 基本统计特征函数

1) sum:计算数据样本的总和（按列计算）

 

D.sum()  #表示按列计算样本D的总和，样本D可为DataFrame或者Series

 

2) mean：计算数据样本的算术平均数

 

D.mean()  #表示按列计算样本D的均值，样本D可为DataFrame或者Series

 

3) var：方差 

D.var()  #表示按列计算样本D的方差，样本D可为DataFrame或者Series

4) std：标准差

D.std()  #表示按列计算样本D的标准差，样本D可为DataFrame或者Series

5) corr：计算数据样本的Spearman(Pearson)相关系数矩阵。

D.corr(method='pearson')  #method参数为计算方法
S1.corr(S2,method='pearson')   #计算S1，S2之间的相关系数

6) cov：协方差矩阵

D.cov
S1.cov(S2)   #计算S1，S2之间的协方差矩阵

7) skew/kurt：偏度（三阶矩）/峰度（四阶矩）

D.skew()
D.kurt()

8) describe:直接给出样本数据的一些基本统计量

D.describe()    #describe括号里可带参数

3.3.2 拓展统计特征数据

3.3.3 统计绘图函数

1）plot：线性二维图，折线图

#代码3-16
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0,2*np.pi,50)
y = np.sin(x)
plt.plot(x,y,'bp--')
plt.title('3107')
plt.show()

 

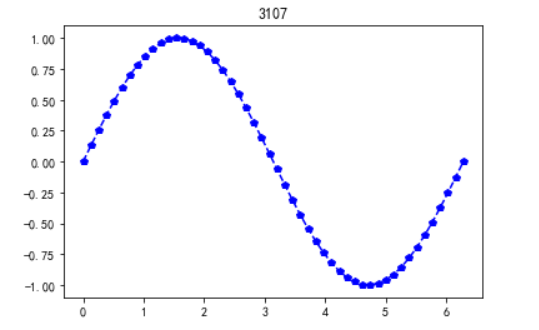
2）pie：饼图

#代码3-17
import matplotlib.pyplot as plt
# The slices will be ordered and plotted counter-clockwise.
labels = 'Frogs','Hogs','Dogs','Logs'   #定义每一块的标签
sizes = [15,30,45,10]   #每一块的比例
colors = ['yellowgreen','gold','lightskyblue','lightcoral']
explode = (0,0.1,0,0)   #突出显示第二块Hogs
plt.pie(sizes,explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True, startangle=90)
plt.axis('equal')      #显示为圆（避免比例压缩为椭圆）
plt.title('3107')
plt.show()

 

 

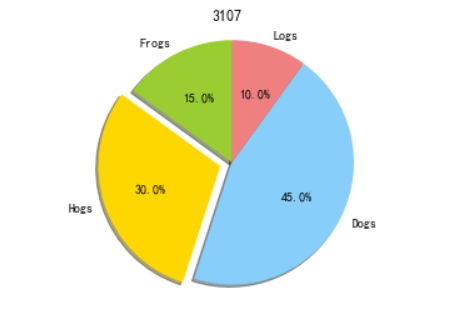
 3）hist：二维条形直方图

#代码3-18
import matplotlib.pyplot as plt
import numpy as np
x = np.random.randn(1000)    #1000个服从正态分布的随机数
plt.hist(x,10)        #分成10组绘制直方图
plt.title('3107')
plt.show()

 

 

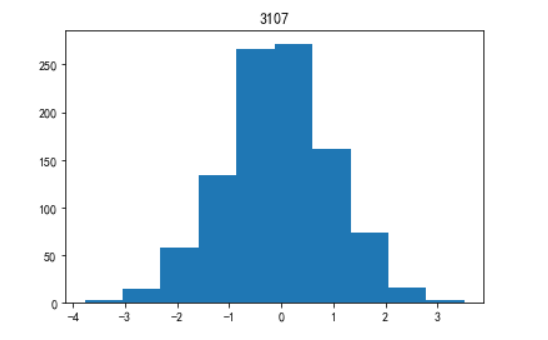
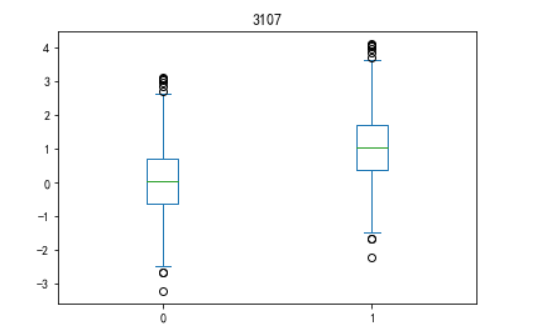
 4）boxplot：箱型图

#代码3-19
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
x = np.random.randn(1000)
D = pd.DataFrame([x,x+1]).T            #构造两列的DataFrame
D.plot(kind='box')           #调用Series内置的绘图方法画图，用kind参数指定箱型图(box)
plt.title('3107')
plt.show()

 

 

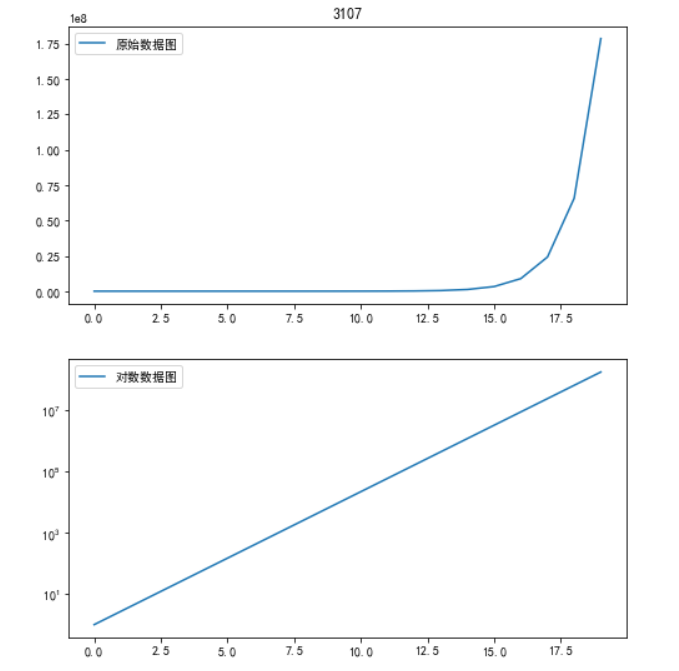
 5）plot(logx=True)/plot(logy=True)：绘制x或y轴的对数图形

# 代码3-20
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

import numpy as np
import pandas as pd
x = pd.Series(np.exp(np.arange(20)))
plt.figure(figsize=(8,9))

axl = plt.subplot(2,1,1)
x.plot(label='原始数据图',legend=True)
plt.title('3107')

axl = plt.subplot(2,1,2)
x.plot(logy=True,label='对数数据图',legend=True)
plt.show()

 

 

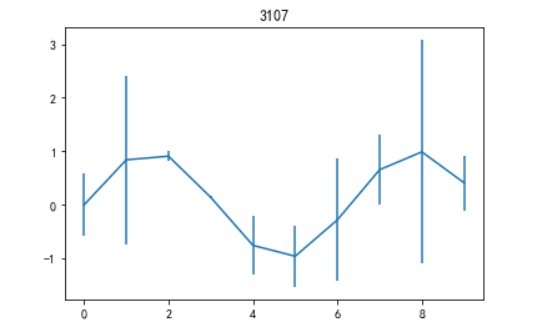
 6）plot(yerr = error)：绘制误差条形图

#代码3-21
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
import numpy as np
import pandas as pd

error = np.random.randn(10)
y = pd.Series(np.sin(np.arange(10)))
y.plot(yerr = error)
plt.title('3107')
plt.show()