PCB genesis连孔加除毛刺孔(槽孔与槽孔)实现方法(三)
一.为什么 连孔加除毛刺孔
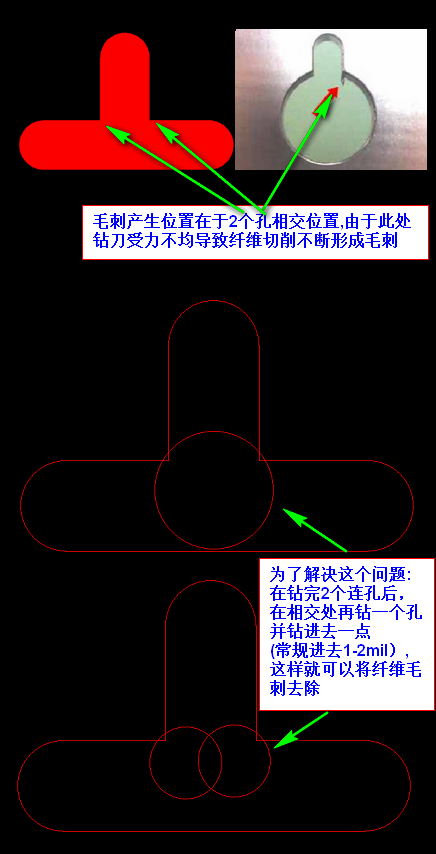
原因是 PCB板材中含有玻璃纤维, 毛刺产生位置在于2个孔相交位置,由于此处钻刀受力不均导致纤维切削不断形成毛刺 ,为了解决这个问题:在钻完2个连孔后,在相交处再钻一个孔,并钻进去一点(常规进去1-2mil),这样就可以将纤维毛刺去除 (没找到SLOT槽与SLOT槽的实物图.就用SLOT槽与圆孔吧,产生毛刺效果也是一样的)
PCB同行业毛刺问题处理办法 钻孔孔内毛刺问题分析改善报告
二.如何判断除毛刺孔加多少个?
在PCB行业工程加除毛刺孔加多少个也没有太明确的定义,只要满足毛刺去除即可.
这里我们把相交的SLOT槽分为2类,一类是十字形,另一类是T型,分别用实际的案例做以说明.
1.十字型交叉SLOT槽:
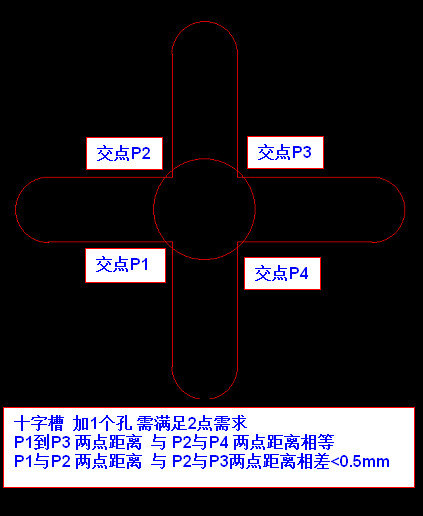
实例1:十字槽 加1个孔 需满足2点需求
P1到P3 两点距离 与 P2与P4 两点距离相等
P1与P2 两点距离 与 P2与P3两点距离相差<0.5mm
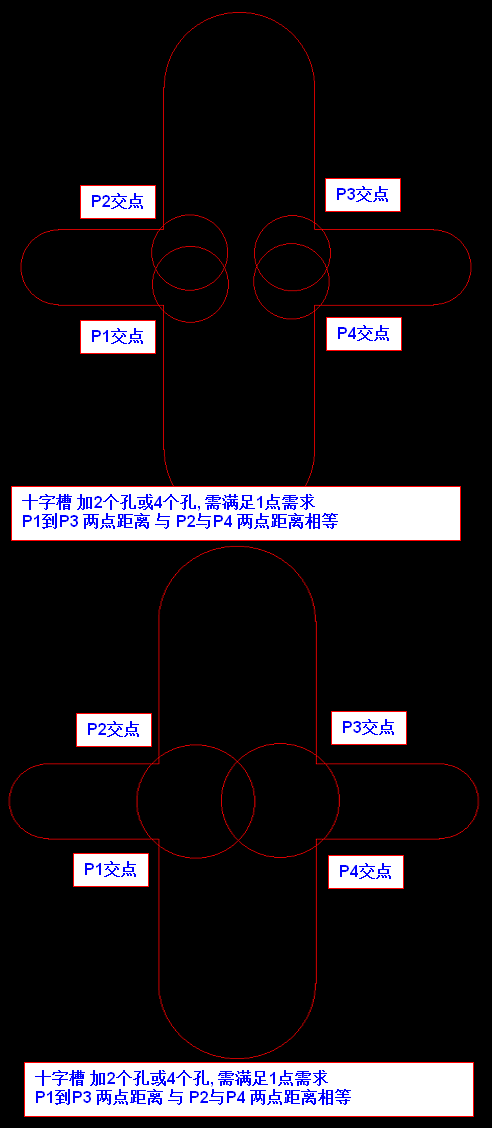
实例2:十字槽 加2个孔或4个孔, 需满足1点需求
P1到P3 两点距离 与 P2与P4 两点距离相等
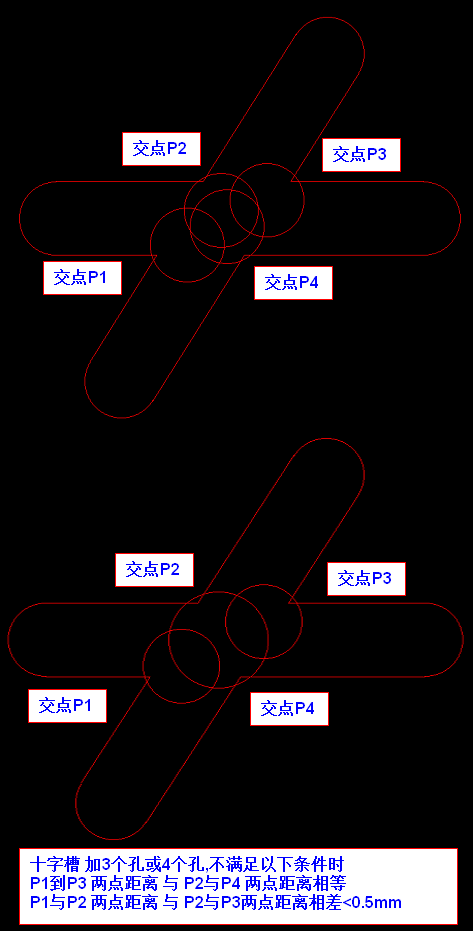
实例3:十字槽 加3个孔或4个孔,不满足以下条件时
P1到P3 两点距离 与 P2与P4 两点距离相等
P1与P2 两点距离 与 P2与P3两点距离相差<0.5mm
失效实例:十字槽钻1个孔失效案例
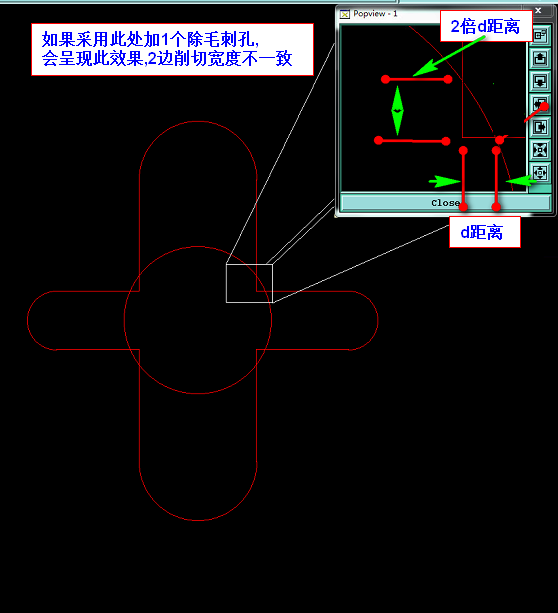
2.T字型交叉SLOT槽:
实例1: T字槽 加1个孔, 需满足以下条件时
(W1 * 0.5 + W1 * 0.707) < W2
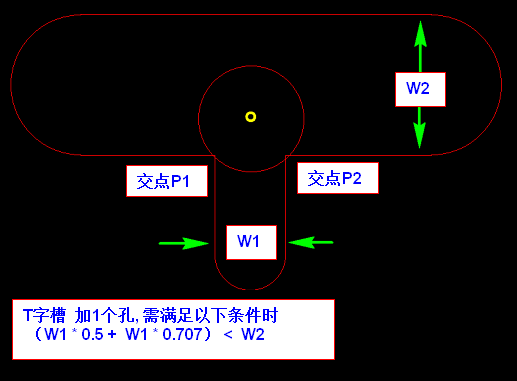
实例2:T字槽 加2个孔, 不满足以下条件时
(W1 * 0.5 + W1 * 0.707) < W2

三.连孔加除毛刺孔实现关键需求出参数
除毛刺孔,这里列举几个关键参数,如下图所示(因为求解的参数太多,画图不好呈现,具体请看下方的代码)
1.T字型槽加1个孔
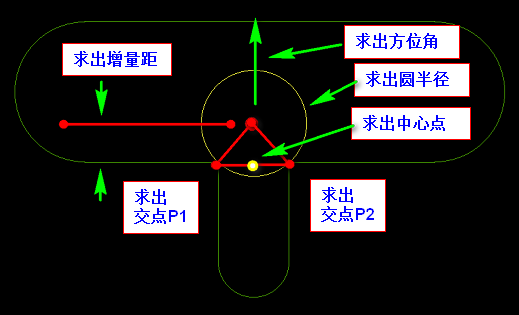
2.T字型槽加2个孔
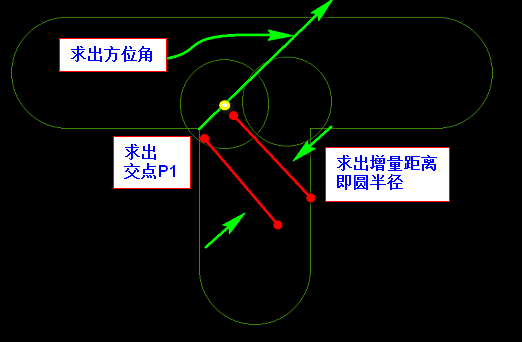
3.十字型槽加孔和T字型加孔类型,具体看下方代码
四.C#简易代码实现:
1.加除毛刺孔代码

#region 加除毛刺孔 mcdrl gLayer glayer = g.getFEATURES($"{"drl"}", g.STEP, g.JOB, "mm", true); gL line1 = glayer.Llist[0]; gL line2 = glayer.Llist[1]; List<gP> gpList = calc2.l2l_IntersectHole(line1, line2, 0.05); addCOM.pad(gpList); #endregion
2.计算函数

/// <summary> /// 线段与线段(2个SLOT槽相交) 加除毛刺孔 /// </summary> /// <param name="l1"></param> /// <param name="l2"></param> /// <param name="CutInner">切入值</param> /// <returns></returns> public List<gP> l2l_IntersectHole(gL l1, gL l2, double CutInner = 0.05) { add addCOM = new add(); List<gP> gpList = new List<gP>(); gL l1_L, l1_R, l2_L, l2_R; int jd1Type = 0, jd2Type = 0, jd3Type = 0, jd4Type = 0; gPoint jdP1, jdP2, jdP3, jdP4; double ang1, ang2, ang3, ang4; gPoint HoleP1, HoleP2, HoleP3, HoleP4; if (multi(l1.ps, l1.pe, l2.ps) < 0 && multi(l1.ps, l1.pe, l2.pe) > 0) { gL tempL = l1; l1 = l2; l2 = tempL; } double l1Rval = l1.width * 0.0005; double l2Rval = l2.width * 0.0005; double Rval = l1Rval > l2Rval ? l2Rval : l1Rval; double Hole_Radius = Rval; double HoleSize = Hole_Radius * 2; l_offset(l1, l1Rval, out l1_L, out l1_R); l_offset(l2, l2Rval, out l2_L, out l2_R); jdP1 = l2l_Intersect(l1_L, l2_R, ref jd1Type); jdP2 = l2l_Intersect(l1_L, l2_L, ref jd2Type); jdP3 = l2l_Intersect(l1_R, l2_L, ref jd3Type); jdP4 = l2l_Intersect(l1_R, l2_R, ref jd4Type); jd1Type = jd1Type < 0 ? 0 : jd1Type; jd2Type = jd2Type < 0 ? 0 : jd2Type; jd3Type = jd3Type < 0 ? 0 : jd3Type; jd4Type = jd4Type < 0 ? 0 : jd4Type; if ((jd1Type + jd2Type + jd3Type + jd4Type) == 4) //产生4个交点 { if (Math.Abs(p2p_di(jdP1, jdP3) - p2p_di(jdP2, jdP4)) < 0.01) //4个交点且交错交点相等时 加1个孔 { if (Math.Abs(p2p_di(jdP1, jdP2) - p2p_di(jdP2, jdP3)) < 0.51) //4个交点且2条槽宽相差小于0.5mm 加1个孔 { gPoint PointCenter = p2p_centerP(jdP1, jdP3); Hole_Radius = p2p_di(PointCenter, jdP1) + CutInner; HoleSize = ((int)(Math.Ceiling((Hole_Radius * 2 * 1000) / 50)) * 50) * 0.001; ; gpList.Add(new gP(PointCenter, HoleSize * 1000)); return gpList; } } } if ((jd1Type + jd2Type + jd3Type + jd4Type) == 2) //产生2个交点 { //P2 P3 //P1 P4 gPoint LineCenter = new gPoint(); double AngDirdction = 0; double ValDirdction = 0; double ValR = 0; double Lwidth = 0; if (jd1Type + jd2Type == 2) { LineCenter = p2p_centerP(jdP1, jdP2); AngDirdction = p_ang(LineCenter, l1_R); ValDirdction = p2p_di(jdP1, jdP2) * 0.5; ValR = ValDirdction * 1.4142136; Lwidth = l1Rval * 2; } if (jd2Type + jd3Type == 2) { LineCenter = p2p_centerP(jdP2, jdP3); AngDirdction = p_ang(LineCenter, l2_R); ValDirdction = p2p_di(jdP2, jdP3) * 0.5; ValR = ValDirdction * 1.4142136; Lwidth = l2Rval * 2; } if (jd3Type + jd4Type == 2) { LineCenter = p2p_centerP(jdP3, jdP4); AngDirdction = p_ang(LineCenter, l1_L); ValDirdction = p2p_di(jdP3, jdP4) * 0.5; ValR = ValDirdction * 1.4142136; Lwidth = l1Rval * 2; } if (jd4Type + jd1Type == 2) { LineCenter = p2p_centerP(jdP4, jdP1); AngDirdction = p_ang(LineCenter, l2_L); ValDirdction = p2p_di(jdP4, jdP1) * 0.5; ValR = ValDirdction * 1.4142136; Lwidth = l2Rval * 2; } Hole_Radius = ValR + CutInner; HoleSize = ((int)(Math.Ceiling((Hole_Radius * 2 * 1000) / 50)) * 50) * 0.001; Hole_Radius = HoleSize * 0.5; double diffVal = Hole_Radius - (ValR + CutInner); if (diffVal > 0) { ValDirdction = Math.Sqrt(Math.Pow((ValR + diffVal), 2) - Math.Pow((ValDirdction), 2)); } if ((ValDirdction + Hole_Radius - 0.1) < Lwidth) //2个交点且正交时 加1个孔 { gPoint PointCenter = p_val_ang(LineCenter, ValDirdction, AngDirdction); gpList.Add(new gP(PointCenter, HoleSize * 1000)); return gpList; } } //当不满足条件的,全按一个交点加一个孔的方式处理 HoleSize = ((int)(Math.Ceiling((Rval * 2 * 1000) / 50)) * 50) * 0.001; Hole_Radius = HoleSize * 0.5; ang1 = a_AngleCenter_dirdction(jdP2, jdP1, jdP4); ang2 = a_AngleCenter_dirdction(jdP3, jdP2, jdP1); ang3 = p_ang_invert(ang1); ang4 = p_ang_invert(ang2); HoleP1 = p_val_ang(jdP1, Hole_Radius - CutInner, ang1); HoleP2 = p_val_ang(jdP2, Hole_Radius - CutInner, ang2); HoleP3 = p_val_ang(jdP3, Hole_Radius - CutInner, ang3); HoleP4 = p_val_ang(jdP4, Hole_Radius - CutInner, ang4); if (jd1Type == 1) gpList.Add(new gP(HoleP1, HoleSize * 1000)); if (jd2Type == 1) gpList.Add(new gP(HoleP2, HoleSize * 1000)); if (jd3Type == 1) gpList.Add(new gP(HoleP3, HoleSize * 1000)); if (jd4Type == 1) gpList.Add(new gP(HoleP4, HoleSize * 1000)); return gpList; } /// <summary> /// 线Line偏移 out 左与右偏移线Line /// </summary> /// <param name="l"></param> /// <param name="offset_val">偏移数值</param> /// <param name="left_l">out 左偏移线L</param> /// <param name="rithg_l">out 右偏移线L</param> public void l_offset(gL l, double offset_val, out gL left_l, out gL rithg_l) { left_l = l; rithg_l = l; double angle_ = p_ang(l.ps, l.pe); left_l.ps = p_val_ang(l.ps, offset_val, angle_ + 90); left_l.pe = p_val_ang(l.pe, offset_val, angle_ + 90); rithg_l.ps = p_val_ang(l.ps, offset_val, angle_ - 90); rithg_l.pe = p_val_ang(l.pe, offset_val, angle_ - 90); } /// <summary> /// 求方位角 /// </summary> /// <param name="ps"></param> /// <param name="pe"></param> /// <returns></returns> public double p_ang(gPoint ps, gPoint pe) { double a_ang = Math.Atan((pe.y - ps.y) / (pe.x - ps.x)) / Math.PI * 180; //象限角 转方位角 计算所属象限 并求得方位角 if (pe.x >= ps.x && pe.y >= ps.y) //↗ 第一象限 { return a_ang; } else if (!(pe.x >= ps.x) && pe.y >= ps.y) // ↖ 第二象限 { return a_ang + 180; } else if (!(pe.x >= ps.x) && !(pe.y >= ps.y)) //↙ 第三象限 { return a_ang + 180; } else if (pe.x >= ps.x && !(pe.y >= ps.y)) // ↘ 第四象限 { return a_ang + 360; } else { return a_ang; } }//求方位角 /// <summary> /// 求增量坐标 /// </summary> /// <param name="ps">起点</param> /// <param name="val">增量值</param> /// <param name="ang_direction">角度</param> /// <returns></returns> public gPoint p_val_ang(gPoint ps, double val, double ang_direction) { gPoint pe; pe.x = ps.x + val * Math.Cos(ang_direction * Math.PI / 180); pe.y = ps.y + val * Math.Sin(ang_direction * Math.PI / 180); return pe; } /// <summary> /// 求线段与线段相交点 (线段与线段相差微小距离误差无法可控 之前测试有发现后来没发现了,有待验证) /// </summary> /// <param name="L1"></param> /// <param name="L2"></param> /// <param name="isIntersectType">0平行无交点 1本身相交 -1本身不相交(但延长相交)</param> /// <returns></returns> public gPoint l2l_Intersect(gL L1, gL L2, ref int isIntersectType) { return l2l_Intersect(L1.ps, L1.pe, L2.ps, L2.pe, ref isIntersectType); } /// <summary> /// 求线段与线段相交点 (线段与线段相差微小距离误差无法可控 之前测试有发现后来没发现了,有待验证) /// </summary> /// <param name="l1ps"></param> /// <param name="l1pe"></param> /// <param name="l2ps"></param> /// <param name="l2pe"></param> /// <param name="isIntersectType">0平行无交点 1本身相交 -1本身不相交(但延长相交)</param> /// <returns></returns> public gPoint l2l_Intersect(gPoint l1ps, gPoint l1pe, gPoint l2ps, gPoint l2pe, ref int isIntersectType) { gL L1 = new gL(l1ps, l1pe, 0); gL L2 = new gL(l2ps, l2pe, 0); gPoint tempP = new gPoint(); double ABC, ABD, CDA, CDB, T; //面积符号相同则两点在线段同侧,不相交 (对点在线段上的情况,本例当作不相交处理) ABC = (L1.ps.x - L2.ps.x) * (L1.pe.y - L2.ps.y) - (L1.ps.y - L2.ps.y) * (L1.pe.x - L2.ps.x); ABD = (L1.ps.x - L2.pe.x) * (L1.pe.y - L2.pe.y) - (L1.ps.y - L2.pe.y) * (L1.pe.x - L2.pe.x); CDA = (L2.ps.x - L1.ps.x) * (L2.pe.y - L1.ps.y) - (L2.ps.y - L1.ps.y) * (L2.pe.x - L1.ps.x); // 三角形cda 面积的2倍 // 注意: 这里有一个小优化.不需要再用公式计算面积,而是通过已知的三个面积加减得出. CDB = CDA + ABC - ABD; // 三角形cdb 面积的2倍 if (Math.Abs(ABC - ABD) <= 0.000001) { isIntersectType = 0; //平行 return tempP; } else { if ((CDA * CDB <= 0.000001) && (ABC * ABD <= 0.000001)) //本身相交 { isIntersectType = 1; } else { isIntersectType = -1; //延长相交 } } //计算交点 T = CDA / (ABD - ABC); tempP.x = L1.ps.x + T * (L1.pe.x - L1.ps.x); tempP.y = L1.ps.y + T * (L1.pe.y - L1.ps.y); return tempP; } /// <summary> /// 返回两点之间欧氏距离 /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <returns></returns> public double p2p_di(gPoint p1, gPoint p2) { return Math.Sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y)); } /// <summary> /// 求点到点 中心点P /// </summary> /// <param name="l"></param> /// <returns></returns> public gPoint p2p_centerP(gPoint p1, gPoint p2) { gPoint tempP; tempP.x = (p1.x + p2.x) * 0.5; tempP.y = (p1.y + p2.y) * 0.5; return tempP; } /// <summary> /// 求增量坐标 /// </summary> /// <param name="ps">起点</param> /// <param name="val">增量值</param> /// <param name="ang_direction">角度</param> /// <returns></returns> public gPoint p_val_ang(gPoint ps, double val, double ang_direction) { gPoint pe; pe.x = ps.x + val * Math.Cos(ang_direction * Math.PI / 180); pe.y = ps.y + val * Math.Sin(ang_direction * Math.PI / 180); return pe; } /// <summary> /// 求弧Arc 弧中心方位角 /// </summary> /// <param name="ps"></param> /// <param name="pc"></param> /// <param name="pe"></param> /// <param name="ccw"></param> /// <returns></returns> public double a_AngleCenter_dirdction(gPoint ps, gPoint pc, gPoint pe, bool ccw = false) { double angle_s, angle_e, angle_sum, center_dirdction; if (ccw) { angle_s = p_ang(pc, pe); angle_e = p_ang(pc, ps); } else { angle_s = p_ang(pc, ps); angle_e = p_ang(pc, pe); } if (angle_s == 360) { angle_s = 0; } if (angle_e >= angle_s) { angle_sum = 360 - (angle_e - angle_s); center_dirdction = (angle_s + angle_e) * 0.5 + 180; } else { angle_sum = angle_s - angle_e; center_dirdction = (angle_s + angle_e) * 0.5; } if (center_dirdction > 360) { center_dirdction = center_dirdction - 360; } return center_dirdction; } /// <summary> /// 求反方位角 /// </summary> /// <param name="ang_direction"></param> /// <returns></returns> public double p_ang_invert(double ang_direction)//求反方位角 { if (ang_direction >= 180) return ang_direction - 180; else return ang_direction + 180; }
3.Point,PAD;Line;Arc数据结构

/// <summary> /// Line 数据类型 /// </summary> public struct gL { public gL(double ps_x, double ps_y, double pe_x, double pe_y, double width_) { this.ps = new gPoint(ps_x, ps_y); this.pe = new gPoint(pe_x, pe_y); this.negative = false; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gL(gPoint ps_, gPoint pe_, double width_) { this.ps = ps_; this.pe = pe_; this.negative = false; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gL(gPoint ps_, gPoint pe_, string symbols_, double width_) { this.ps = ps_; this.pe = pe_; this.negative = false; this.symbols = symbols_; this.attribut = string.Empty; this.width = width_; } public gPoint ps; public gPoint pe; public bool negative;//polarity-- positive negative public string symbols; public string attribut; public double width; public static gL operator +(gL l1, gPoint move_p) { l1.ps += move_p; l1.pe += move_p; return l1; } public static gL operator +(gL l1, gP move_p) { l1.ps += move_p.p; l1.pe += move_p.p; return l1; } public static gL operator -(gL l1, gPoint move_p) { l1.ps -= move_p; l1.pe -= move_p; return l1; } public static gL operator -(gL l1, gP move_p) { l1.ps -= move_p.p; l1.pe -= move_p.p; return l1; } } /// <summary> /// ARC 数据类型 /// </summary> public struct gA { public gA(double ps_x, double ps_y, double pc_x, double pc_y, double pe_x, double pe_y, double width_, bool ccw_) { this.ps = new gPoint(ps_x, ps_y); this.pc = new gPoint(pc_x, pc_y); this.pe = new gPoint(pe_x, pe_y); this.negative = false; this.ccw = ccw_; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gA(gPoint ps_, gPoint pc_, gPoint pe_, double width_, bool ccw_ = false) { this.ps = ps_; this.pc = pc_; this.pe = pe_; this.negative = false; this.ccw = ccw_; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gPoint ps; public gPoint pe; public gPoint pc; public bool negative;//polarity-- positive negative public bool ccw; //direction-- cw ccw public string symbols; public string attribut; public double width; public static gA operator +(gA arc1, gPoint move_p) { arc1.ps += move_p; arc1.pe += move_p; arc1.pc += move_p; return arc1; } public static gA operator +(gA arc1, gP move_p) { arc1.ps += move_p.p; arc1.pe += move_p.p; arc1.pc += move_p.p; return arc1; } public static gA operator -(gA arc1, gPoint move_p) { arc1.ps -= move_p; arc1.pe -= move_p; arc1.pc -= move_p; return arc1; } public static gA operator -(gA arc1, gP move_p) { arc1.ps -= move_p.p; arc1.pe -= move_p.p; arc1.pc -= move_p.p; return arc1; } } /// <summary> /// PAD 数据类型 /// </summary> public struct gP { public gP(double x_val, double y_val, double width_) { this.p = new gPoint(x_val, y_val); this.negative = false; this.angle = 0; this.mirror = false; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gPoint p; public bool negative;//polarity-- positive negative public double angle; public bool mirror; public string symbols; public string attribut; public double width; public static gP operator +(gP p1, gP p2) { p1.p += p2.p; return p1; } public static gP operator -(gP p1, gP p2) { p1.p -= p2.p; return p1; } } /// <summary> /// 点 数据类型 (XY) /// </summary> public struct gPoint { public gPoint(gPoint p_) { this.x = p_.x; this.y = p_.y; } public gPoint(double x_val, double y_val) { this.x = x_val; this.y = y_val; } public double x; public double y; public static gPoint operator +(gPoint p1, gPoint p2) { p1.x += p2.x; p1.y += p2.y; return p1; } public static gPoint operator -(gPoint p1, gPoint p2) { p1.x -= p2.x; p1.y -= p2.y; return p1; } }
五.在Genesis或Incam中如何判断是否为连孔
判断2个孔是否为连孔,可以自己写算法实现啦,当然更多人还是会选择奥宝提供DrillChecklist分析出来的的结果来判断是否为连孔.因为你自己写的算法效率没有奥宝的效率高呀

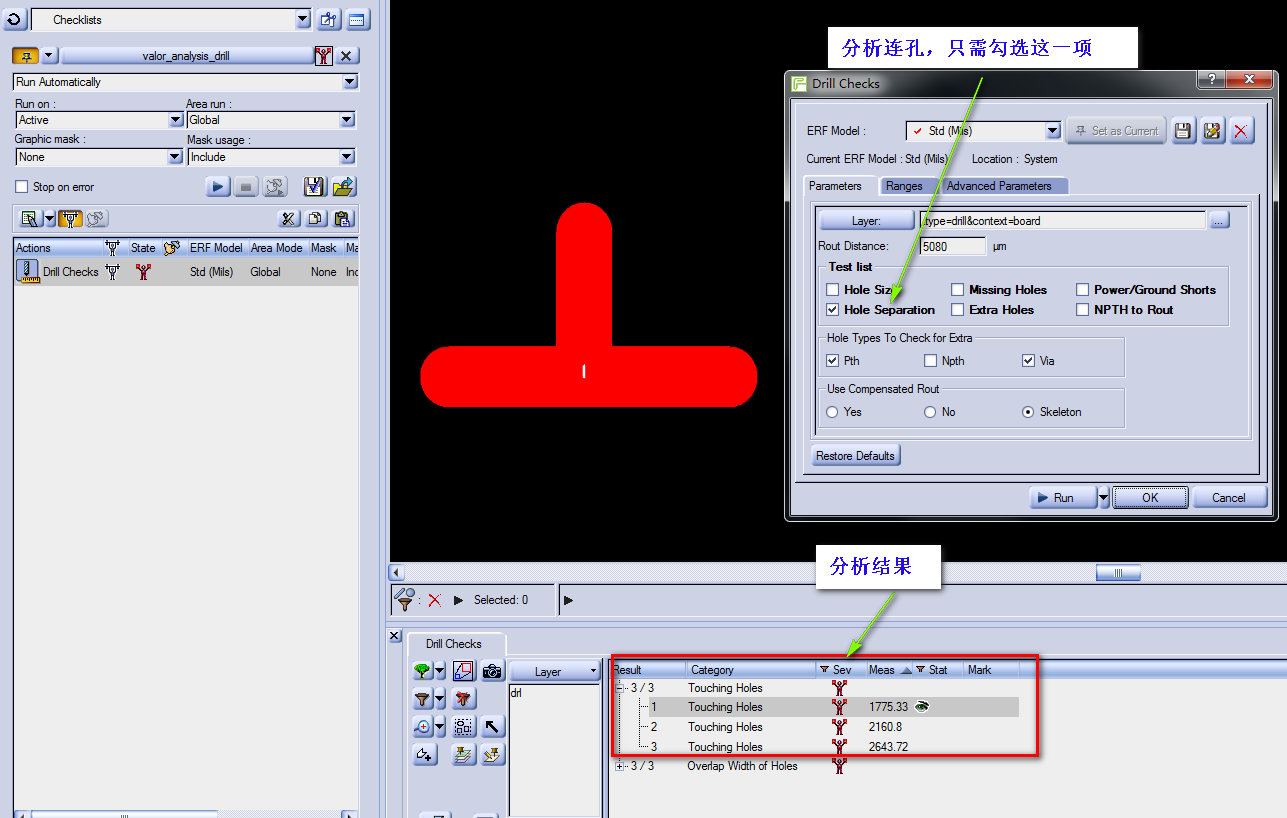
六.实现效果
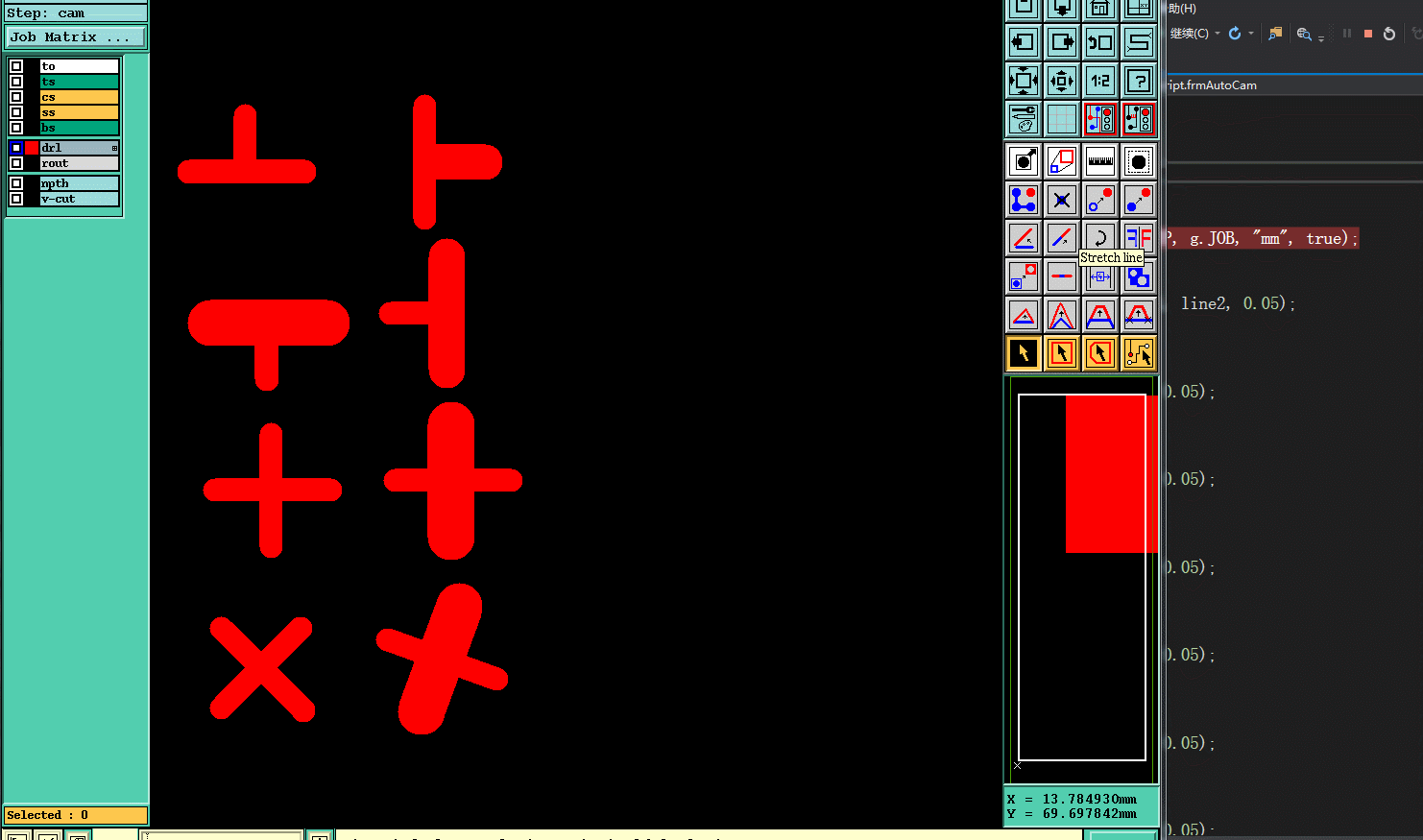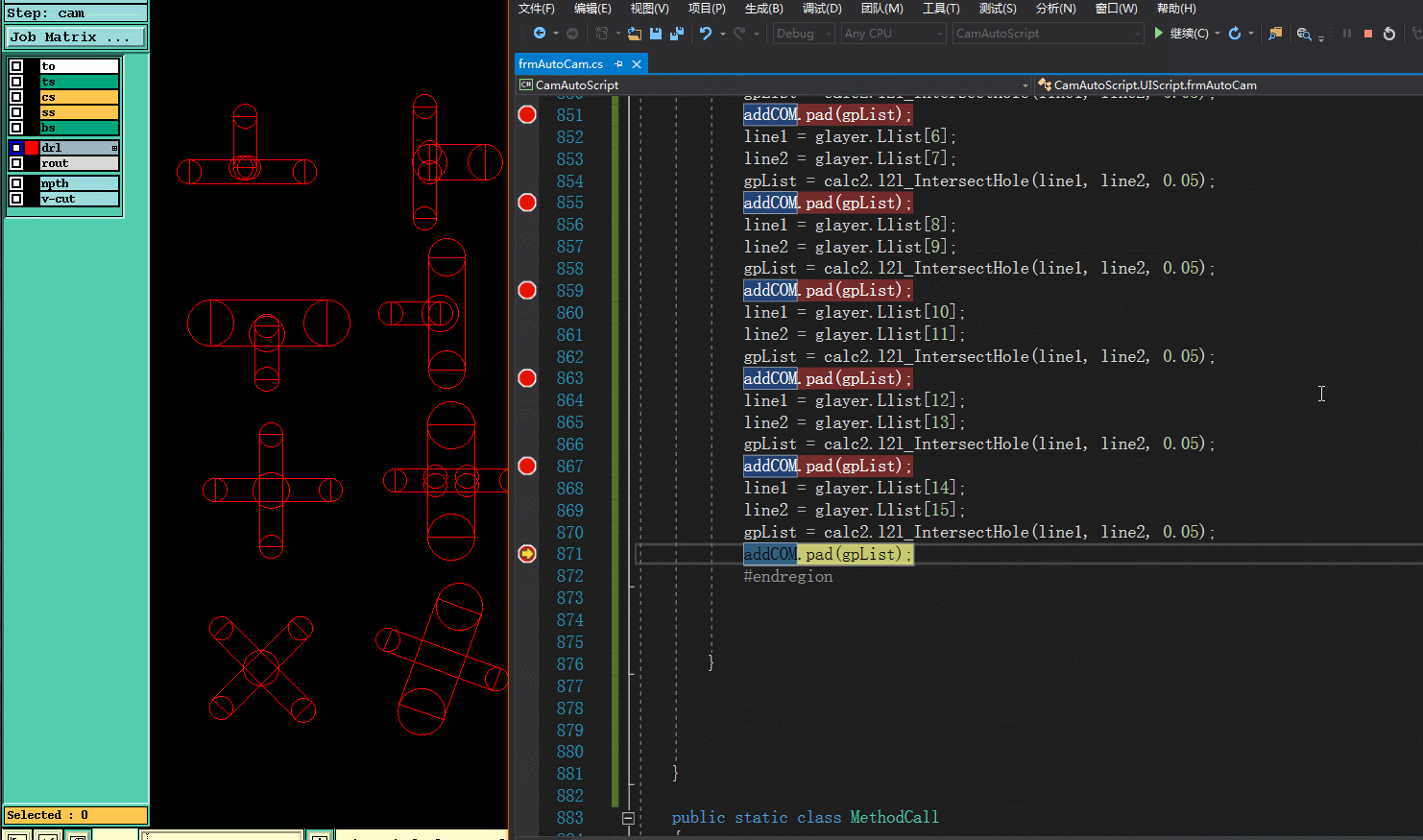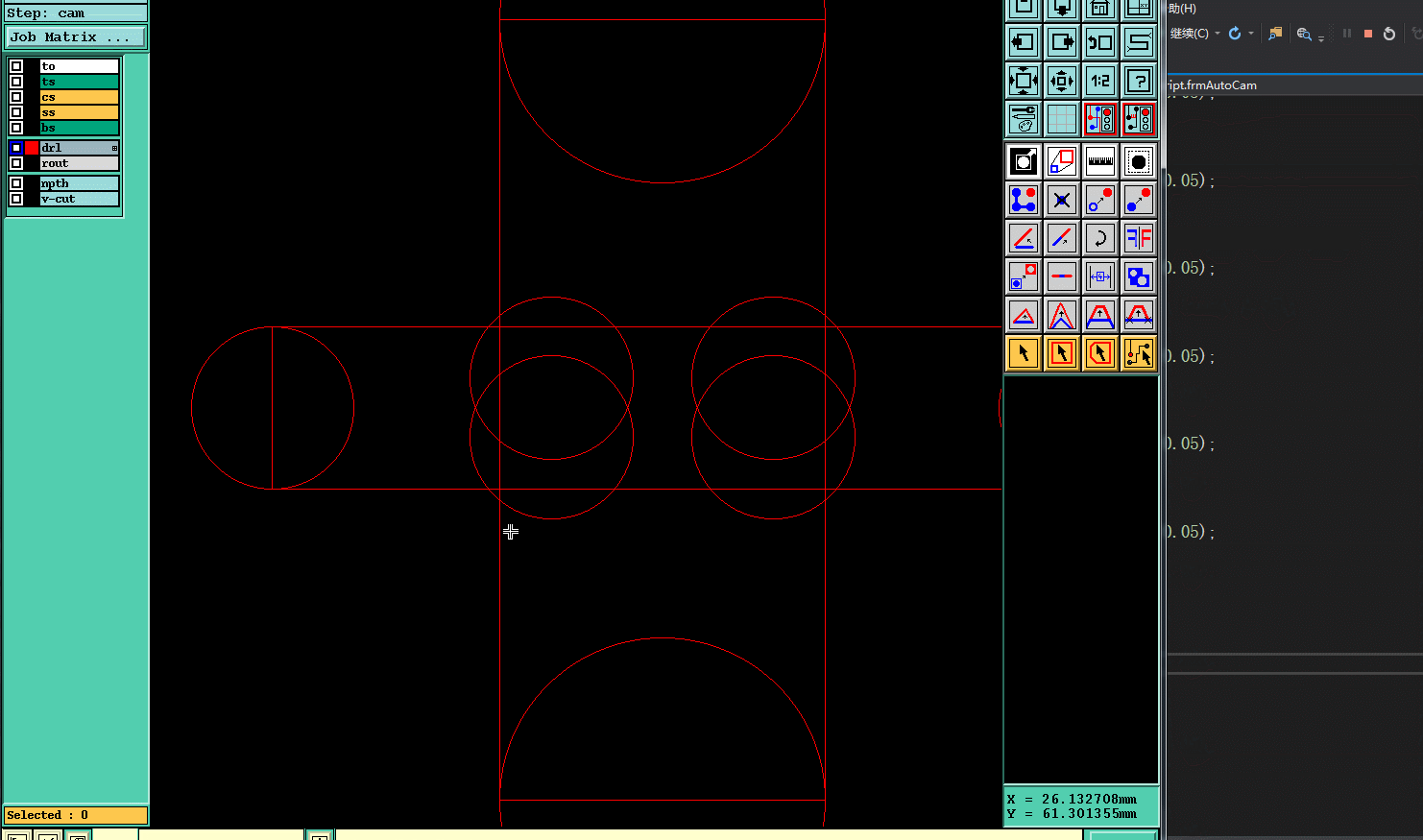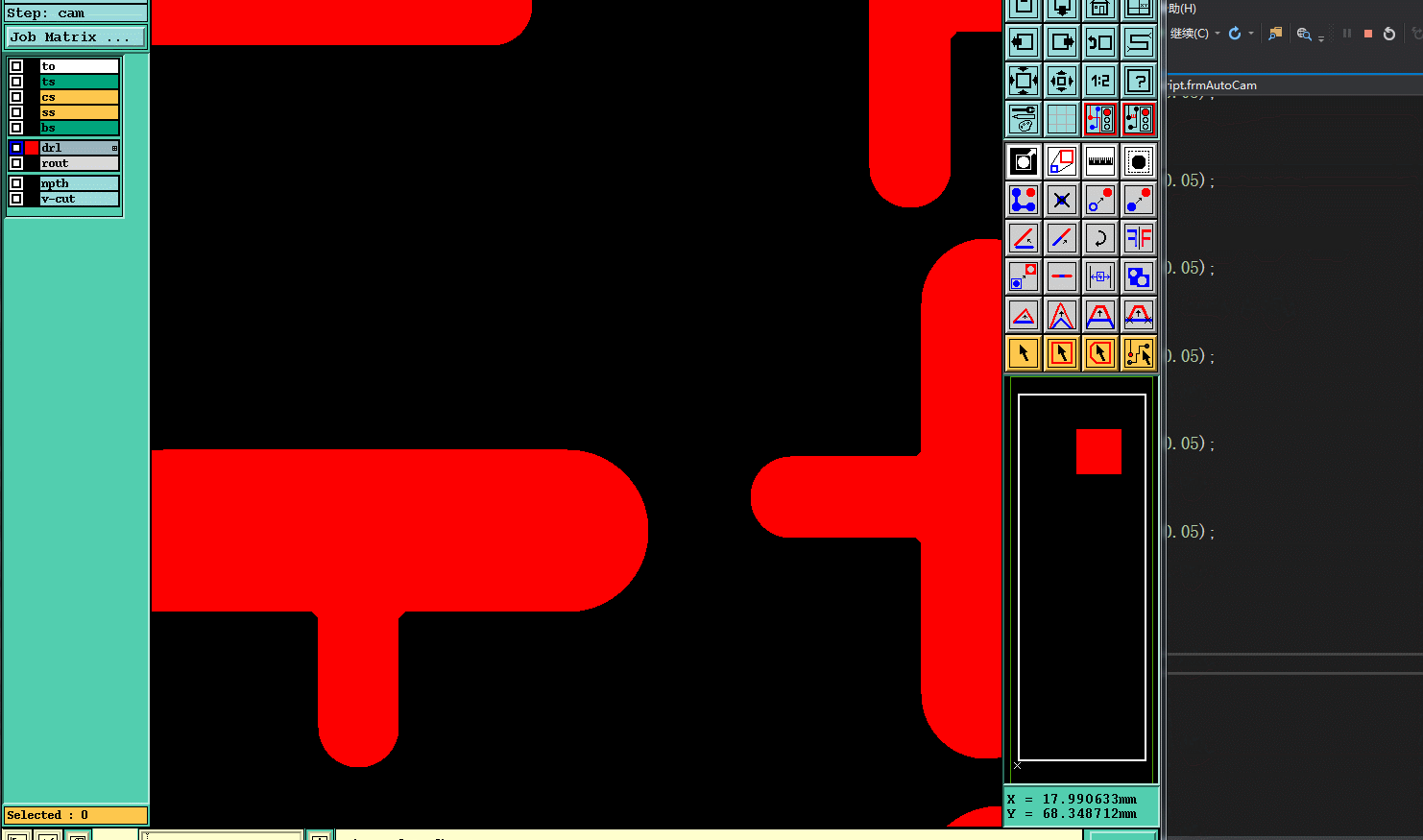
作者:pcbren 微信号:yadnfku QQ号: 254566449

博客地址:https://www.cnblogs.com/pcbren/
声明:本博客原创文字只代表本人工作中在某一时间内总结的观点或结论,与本人所在单位没有直接利益关系。非商业,未授权,贴子请以现状保留,转载时必须保留此段声明,且在文章页面明显位置给出原文连接。
如果大家感觉我的博文对大家有帮助,请推荐支持一把。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号