余弦距离、欧氏距离和杰卡德相似性度量的对比分析(转)
1、余弦距离
余弦距离,也称为余弦相似度,是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。
向量,是多维空间中有方向的线段,如果两个向量的方向一致,即夹角接近零,那么这两个向量就相近。而要确定两个向量方向是否一致,这就要用到余弦定理计算向量的夹角。
余弦定理描述了三角形中任何一个夹角和三个边的关系。给定三角形的三条边,可以使用余弦定理求出三角形各个角的角度。假定三角形的三条边为a,b和c,对应的三个角为A,B和C,那么角A的余弦为:
如果将三角形的两边b和c看成是两个向量,则上述公式等价于:
其中分母表示两个向量b和c的长度,分子表示两个向量的内积。
举一个具体的例子,假如新闻X和新闻Y对应向量分别是:
x1, x2, ..., x6400和
y1, y2, ..., y6400
则,它们之间的余弦距离可以用它们之间夹角的余弦值来表示:
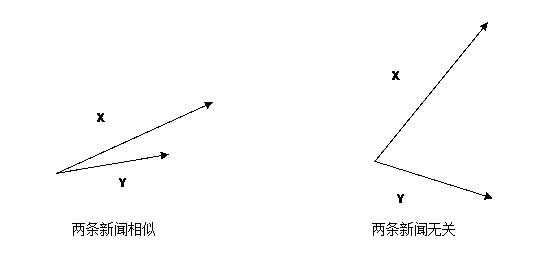
当两条新闻向量夹角余弦等于1时,这两条新闻完全重复(用这个办法可以删除爬虫所收集网页中的重复网页);当夹角的余弦值接近于1时,两条新闻相似(可以用作文本分类);夹角的余弦越小,两条新闻越不相关。
2、余弦距离和欧氏距离的对比
从上图可以看出,余弦距离使用两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比欧氏距离,余弦距离更加注重两个向量在方向上的差异。
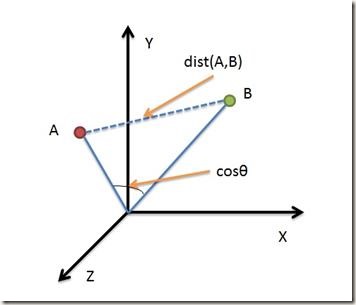
借助三维坐标系来看下欧氏距离和余弦距离的区别:
从上图可以看出,欧氏距离衡量的是空间各点的绝对距离,跟各个点所在的位置坐标直接相关;而余弦距离衡量的是空间向量的夹角,更加体现在方向上的差异,而不是位置。如果保持A点位置不变,B点朝原方向远离坐标轴原点,那么这个时候余弦距离 ![]() 是保持不变的(因为夹角没有发生变化),而A、B两点的距离显然在发生改变,这就是欧氏距离和余弦距离之间的不同之处。
是保持不变的(因为夹角没有发生变化),而A、B两点的距离显然在发生改变,这就是欧氏距离和余弦距离之间的不同之处。
欧氏距离和余弦距离各自有不同的计算方式和衡量特征,因此它们适用于不同的数据分析模型:
欧氏距离能够体现个体数值特征的绝对差异,所以更多的用于需要从维度的数值大小中体现差异的分析,如使用用户行为指标分析用户价值的相似度或差异。
余弦距离更多的是从方向上区分差异,而对绝对的数值不敏感,更多的用于使用用户对内容评分来区分兴趣的相似度和差异,同时修正了用户间可能存在的度量标准不统一的问题(因为余弦距离对绝对数值不敏感)。
3、杰卡德相似性度量
(1)杰卡德相似系数
两个集合A和B交集元素的个数在A、B并集中所占的比例,称为这两个集合的杰卡德系数,用符号 J(A,B) 表示。杰卡德相似系数是衡量两个集合相似度的一种指标(余弦距离也可以用来衡量两个集合的相似度)。
(2)杰卡德距离
与杰卡德相似系数相反的概念是杰卡德距离(Jaccard Distance),可以用如下公式来表示:
杰卡德距离用两个两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
(3)杰卡德相似系数的应用
假设样本A和样本B是两个n维向量,而且所有维度的取值都是0或1。例如,A(0,1,1,0)和B(1,0,1,1)。我们将样本看成一个集合,1表示集合包含该元素,0表示集合不包含该元素。
p:样本A与B都是1的维度的个数
q:样本A是1而B是0的维度的个数
r:样本A是0而B是1的维度的个数
s:样本A与B都是0的维度的个数
那么样本A与B的杰卡德相似系数可以表示为:
此处分母之所以不加s的原因在于:
对于杰卡德相似系数或杰卡德距离来说,它处理的都是非对称二元变量。非对称的意思是指状态的两个输出不是同等重要的,例如,疾病检查的阳性和阴性结果。
按照惯例,我们将比较重要的输出结果,通常也是出现几率较小的结果编码为1(例如HIV阳性),而将另一种结果编码为0(例如HIV阴性)。给定两个非对称二元变量,两个都取1的情况(正匹配)认为比两个都取0的情况(负匹配)更有意义。负匹配的数量s认为是不重要的,因此在计算时忽略。
(4)杰卡德相似度算法分析
杰卡德相似度算法没有考虑向量中潜在数值的大小,而是简单的处理为0和1,不过,做了这样的处理之后,杰卡德方法的计算效率肯定是比较高的,毕竟只需要做集合操作。
4、调整余弦相似度算法(Adjusted Cosine Similarity)
余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,因此没法衡量每个维度上数值的差异,会导致这样一种情况:
用户对内容评分,按5分制,X和Y两个用户对两个内容的评分分别为(1,2)和(4,5),使用余弦相似度得到的结果是0.98,两者极为相似。但从评分上看X似乎不喜欢2这个 内容,而Y则比较喜欢,余弦相似度对数值的不敏感导致了结果的误差,需要修正这种不合理性就出现了调整余弦相似度,即所有维度上的数值都减去一个均值,比如X和Y的评分均值都是3,那么调整后为(-2,-1)和(1,2),再用余弦相似度计算,得到-0.8,相似度为负值并且差异不小,但显然更加符合现实。
那么是否可以在(用户-商品-行为数值)矩阵的基础上使用调整余弦相似度计算呢?从算法原理分析,复杂度虽然增加了,但是应该比普通余弦夹角算法要强。
转自:http://www.cnblogs.com/chaosimple/archive/2013/06/28/3160839.html


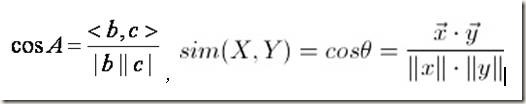
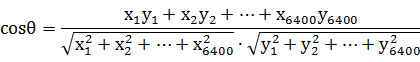
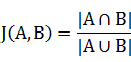
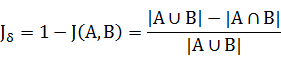
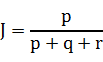

 浙公网安备 33010602011771号
浙公网安备 33010602011771号