20155219 《信息安全系统设计基础》第十四周学习总结
首先我认为第二章 信息的表示和处理 我学的比较差。
当时学的时候有些眼高手低,认为第二章是基础知识,没有把所有精力放在第二章的学习,而是着急去学之后的章节了。故在此重新学习。
1、数字表示
-
无符号编码(unsigned)基于传统的二进制表示法,表示大于或者等于零的数字。
-
补码编码(two’s-complement)表示有符号整数,可以为正负。
-
浮点数编码(floating-point)表示实数的科学计数法的以2为基数版本。
计算机的表示法是用有限数量的位来对一个数字编码。当结果太大以至于不能表示时就会溢出(overflow)。
- 信息存储
①、1个字节=8位,大多数计算机将1个字节作为最小的可寻址的存储器单位。(单片机除外)
②、机器级程序将存储器(一般指内存)视为一个非常大的字节数组,称为虚拟存储器。
③、存储器的每个字节由一个唯一的数字标识,称为地址,所有可能地址的集合称为虚拟存储空间。
④、每台计算机都有一个字长:指明整数和指针数据的标称大小,决定了虚拟存储空间的最大值,即决定了寻址范围。
⑤、大小端:
大端法:高字节在低位,低字节在高位。
小端法:低字节在低位,高字节在高位。
eg:x = 0x12345678 在内存上的存储方式:(注间:12是高字节,78是低字节)
- 深入理解大小端
大小端在计算机业界,Endian表示数据在存储器中的存放顺序。百度百科如下叙述之:
大端模式,是指数据的高字节保存在内存的低地址中,而数据的低字节保存在内存的高地址中,这样的存储模式有点儿类似于把数据当作字符串顺序处理:地址由小向大增加,而数据从高位往低位放;
小端模式,是指数据的高字节保存在内存的高地址中,而数据的低字节保存在内存的低地址中,这种存储模式将地址的高低和数据位权有效地结合起来,高地址部分权值高,低地址部分权值低,和我们的逻辑方法一致。
比如整形十进制数字:305419896 ,转化为十六进制表示 : 0x12345678 。其中按着十六进制的话,每两位占8个字节。如图

- 为什么有大小端模式之分呢?
在操作系统中,x86和一般的OS(如windows,FreeBSD,Linux)使用的是小端模式。但比如Mac OS是大端模式。
在计算机系统中,我们是以字节为单位的,每个地址单元都对应着一个字节,一个字节为8bit。但是在C语言中除了8bit的char之外,还有16bit的short型,32bit的long型(要看具体的编译器)。另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于一个字节,那么必然存在着一个如果将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。
-
知道为什么有模式的存在,下面需要了解下具有有什么应用场景:
1、不同端模式的处理器进行数据传递时必须要考虑端模式的不同
2、在网络上传输数据时,由于数据传输的两端对应不同的硬件平台,采用的存储字节顺序可能不一致。所以在TCP/IP协议规定了在网络上必须采用网络字节顺序,也就是大端模式。对于char型数据只占一个字节,无所谓大端和小端。而对于非char类型数据,必须在数据发送到网络上之前将其转换成大端模式。接收网络数据时按符合接受主机的环境接收。
-
判断机器大小端的两种实现方法
思路:利用共用体所有数据都从同一地址开始存储。
代码如下:
#include <stdio.h>
int main(void)
{
int i;
union endian
{
int data;
char ch;
}test;
test.data = 0x12345678;
if(test.ch == 0x78)
{
printf("little endian!\n");
}
else
{
printf("big endian!\n");
}
for(i=0; i<4; i++)
{
printf("%#x ------- %p\n",*((char *)&test.data + i),(char *)&test.data + i);
}
return 0;
}
实现如下图:
所以Linux是小端的
现在许多处理器都使用双端法,即用户可以通过配置来决定使用大端存储还是小端存储。
PS: 有一点需要注意的是:
UDP/TCP/IP协议规定网络字节序是大端法。进行网络编程的时候,发送数据时需要将本地字节序转换成网络字节序,接收到数据后需要将网络字节序转换成本地字节序。
3.C语言中的位运算
C语言位运算符:与、或、异或、取反、左移和右移。
位运算是指按二进制进行的运算。在系统软件中,常常需要处理二进制位的问题。C语言提供了6个位操作运算符。这些运算符只能用于整型操作数,即只能用于带符号或无符号的char,short,int与long类型。
位运算符列表:
1.& 按位与 如果两个相应的二进制位都为1,则该位的结果值为1,否则为0
2.| 按位或
两个相应的二进制位中只要有一个为1,该位的结果值为1
3.^ 按位异或 若参加运算的两个二进制位值相同则为0,否则为1
4.~ 取反 ~是一元运算符,用来对一个二进制数按位取反,即将0变1,将1变0
5.<< 左移 用来将一个数的各二进制位全部左移N位,右补0
6.>> 右移 将一个数的各二进制位右移N位,移到右端的低位被舍弃,对于无符号数,高位补0
1、“按位与”运算符(&)
按位与是指:参加运算的两个数据,按二进制位进行“与”运算。如果两个相应的二进制位都为1,则该位的结果值为1;否则为0。这里的1可以理解为逻辑中的true,0可以理解为逻辑中的false。按位与其实与逻辑上“与”的运算规则一致。逻辑上的“与”,要求运算数全真,结果才为真。
- 按位与的用途:
(1)清零
c语言源代码:
#include <stdio.h>
main()
{
int a=43;
int b = 148;
printf("%d",a&b);
}
(2)取一个数中某些指定位
若有一个整数a(2byte),想要取其中的低字节,只需要将a与8个1按位与即可。
a 00101100 10101100
b 00000000 11111111
c 00000000 10101100
(3)保留指定位:
与一个数进行“按位与”运算,此数在该位取1.
c语言源代码:
#include <stdio.h>
main()
{
int a=84;
int b = 59;
printf("%d",a&b);
}
2、“按位或”运算符(|)
两个相应的二进制位中只要有一个为1,该位的结果值为1。借用逻辑学中或运算的话来说就是,一真为真。
应用:按位或运算常用来对一个数据的某些位定值为1。例如:如果想使一个数a的低4位改为1,则只需要将a与17(8)进行按位或运算即可。
交换两个值,不用临时变量
① 执行前两个赋值语句:“a=a∧b;”和“b=b∧a;”相当于b=b∧(a∧b)。
② 再执行第三个赋值语句: a=a∧b。由于a的值等于(a∧b),b的值等于(b∧a∧b),
因此,相当于a=a∧b∧b∧a∧b,即a的值等于a∧a∧b∧b∧b,等于b。
c语言源代码:
#include <stdio.h>
main()
{
int a=3;
int b = 4;
a=a^b;
b=b^a;
a=a^b;
printf("a=%d b=%d",a,b);
}
4、“取反”运算符(~)
源代码:
#include <stdio.h>
main()
{
int a=077;
printf("%d",~a);
}
5、左移运算符(<<)
左移运算符是用来将一个数的各二进制位左移若干位,移动的位数由右操作数指定(右操作数必须是非负值),其右边空出的位用0填补,高位左移溢出则舍弃该高位。
左移1位相当于该数乘以2,左移2位相当于该数乘以2*2=4,15<<2=60,即乘了 4。但此结论只适用于该
数左移时被溢出舍弃的高位中不包含1的情况。
假设以一个字节(8位)存一个整数,若a为无符号整型变量,则a=64时,左移一位时溢出的是0,而左移2位时,溢出的高位中包含1。
6、右移运算符(>>)
右移运算符是用来将一个数的各二进制位右移若干位,移动的位数由右操作数指定(右操作数必须是非负
值),移到右端的低位被舍弃,对于无符号数,高位补0。对于有符号数,某些机器将对左边空出的部分
用符号位填补(即“算术移位”),而另一些机器则对左边空出的部分用0填补(即“逻辑移位”)。注
意:对无符号数,右移时左边高位移入0;对于有符号的值,如果原来符号位为0(该数为正),则左边也是移
入0。如果符号位原来为1(即负数),则左边移入0还是1,要取决于所用的计算机系统。有的系统移入0,有的
系统移入1。移入0的称为“逻辑移位”,即简单移位;移入1的称为“算术移位”。
C语言标准并没有明确规定应该使用哪种类型的右移。对于无符号数据(unsigned声明的整型对象),右移必须是逻辑的。而对于有符号的数据,算术或逻辑都可以,因此潜在右移可移植性问题。但实际上,几乎所有编译器/机器组合,对有符号数据的右移都采用算术右移。
Java做得似乎更好一些,因为它对右移操作有明确的定义:x >> k 将x算术右移k个位置,x>>>k将x逻辑右移k个位置。
-
4.整数表示及运算
1.无符号数和有符号数的范围区别
无符号数中,所有的位都用于直接表示该值的大小。有符号数中最高位用于表示正负,所以,当为正值时,该数的最大值就会变小。我们举一个字节的数值对比:
无符号数: 1111 1111 值:255 1* 27 + 1* 26 + 1* 25 + 1* 24 + 1* 23 + 1* 22 + 1* 21 + 1* 20
有符号数: 0111 1111 值:127 1* 26 + 1* 25 + 1* 24 + 1* 23 + 1* 22 + 1* 21 + 1* 20
同样是一个字节,无符号数的最大值是255,而有符号数的最大值是127。原因是有符号数中的最高位被挪去表示符号了。并且,我们知道,最高位的权值也是最高的(对于1字节数来说是2的7次方=128),所以仅仅少于一位,最大值一下子减半。
不过,有符号数的长处是它可以表示负数。因此,虽然它的在最大值缩水了,却在负值的方向出现了伸展。我们仍一个字节的数值对比:
无符号数: 0 ----------------- 255
有符号数: -128 --------- 0 ---------- 127
C允许无符号数和有符号数之间的转换,原则是位表示保持不变。这些转换可以是显示的或隐式的。如下列代码:
int tx,ty
unsigned ux,uy;
tx = (int)ux;
uy = (unsigned)ty;//显示
tx = ux;
uy = ty;//隐式
当用printf输出一个整数时,按照整数的编码根据不同的指示符分别输出int类型(%d)、unsigned类型(%u)或十六进制格式(%x)
int x = -1;
unsigned u = 2147483648;
printf("x = %u = %d = %x\n",x,x,x);
printf("u = %u = %d = %x\n",u,u,u);
得到如下结果:
对于大多数C语言实现,处理同样位长的有符号数(补码)和无符号数间转换规则是:位模式不变,改变解释这些位的方式
- 计算机中的带符号数一般用补码表示
计算机中的带符号数用补码表示的优点:
1、负数的补码与对应正数的补码之间的转换可以用同一种方法——求补运算完成,可以简化硬件;
2、可将减法变为加法,省去减法器;
3、无符号数及带符号数的加法运算可以用同一电路完成。
原码d的通俗定义 :将数的符号数码化,即用一个二进制位表示符号:对正数,该位取0,对负数,该位取1。
反码:正数的反码为原码,负数的反码是原码符号位外按位取反。
补码 定义正数的补码就是它本身,符号位取0,即和原码相同。这就是补码的通俗定义。将这个定义用数学形式表示出来,就可得到补码的正规定义: 其中n为补码的位数。这个定义实际也将真值的范围给出来了,当n=8时,一27≤x<27。和原码相比,补码表示可多表示一个数。当n=8时,多表示的数是一27=一128。
-
5.浮点数
先看下面几个问题:
- 计算机中怎样表示浮点数的,与整型的表示方法有什么不同?
- 32位精度的float类型和64位精度的double类型能表示浮点数最大范围是多少?
- 该C语言语句 printf("%d\n", 2.5); 输出结果是什么,为什么?
我先说在此之前我如果回答,答案如下:
- 计算机中有符号整型采用补码进行表示,浮点型怎么表示没想过。
- float类型可以表示-232-1232,double类型可以表示-264-1264。
- 输出格式要求输出整型,而数是浮点型,类型转化之后输出结果为2。
IEEE754标准(以下简称”标准“)是使用最广泛的浮点数运算标准,为许多CPU与浮点运算器所采用。该标准定义了表示浮点数的格式,如下图所示:

二进制浮点数的表示,分成了三个部分:
符号位、指数、尾数,它们的含义可以类比科学计数法。
- 符号位用1位表示,0表示正数,1表示负数;
- 指数采用移码表示(原来的实际的指数值加上一个固定值得到的),这个固定值为2e-1-1(e为指数部分比特长度),之所以加上这个偏移量,是为了将负数变成非负数,这样两个指数的大小很容易就可以比较。
- 尾数采用原码表示,正如上所说,规格化二进制浮点数最高位均为1,那么小数点前这个就没必要用一个比特位去存储,我们默认已经存在,称为”隐藏位“。
标准规定了四种浮点数的表示方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80比特实做)。C语言中float和double浮点型分别对应的是单精度和双精度浮点数,下面介绍这两种浮点数的存储格式:
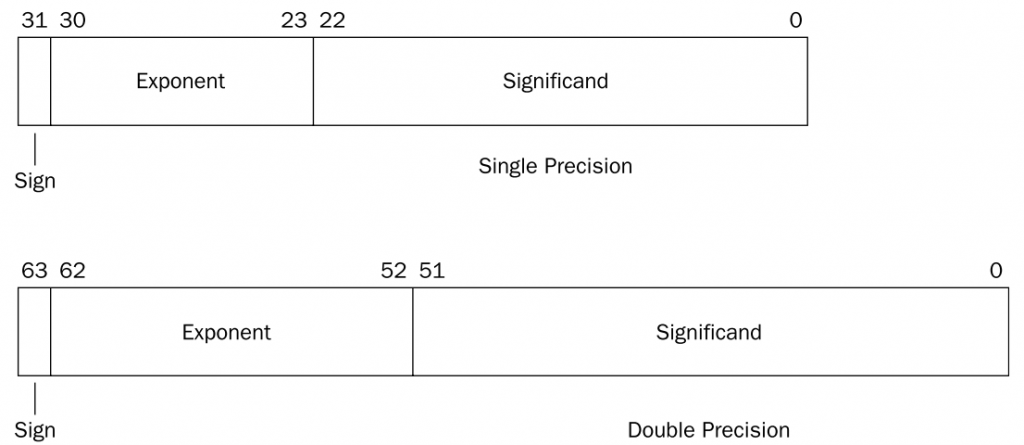
如上面两个例子,分别使用单精度和双精度表示如下:
(1001.0111010)2 = +1.001011101 × 23
单精度: 符号位0,指数位为3+127=130(10000010),尾数1.001011101隐藏最高位1之后为001011101,因此表示为:
0 10000010 00101110100000000000000
双精度:只是在指数位上加的偏移量不同,3+1023=1026(10000000010),表示为:
0 10000000010 0010111010000000000000000000000000000000000000000000
(-0.0001010011)2 = -1.010011 × 2-4
单精度:符号位1,指数位为-4+127=123(1111011),尾数1.010011 隐藏最高位1之后为010011,因此表示为:
0 01111011 01001100000000000000000
双精度:指数位为-4+1023=1019(1111111011),表示为:
0 01111111011 0100110000000000000000000000000000000000000000000000
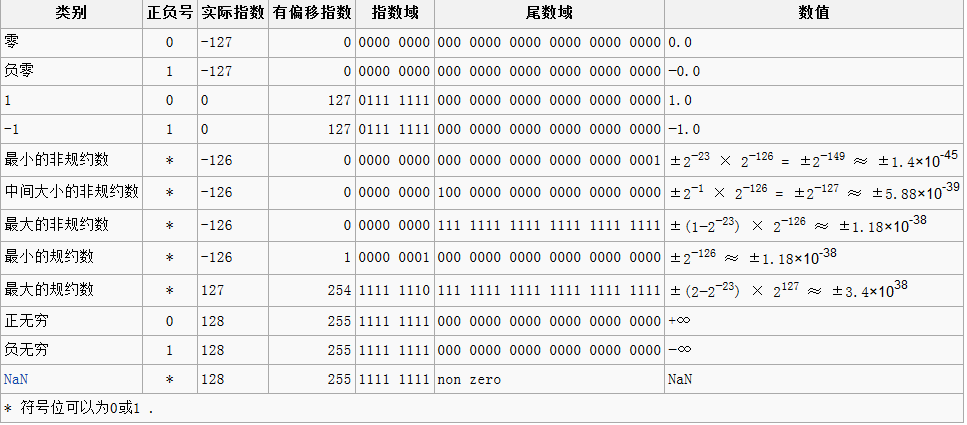
下表为单精度浮点数各种极值情况:
我们写一个C语言程序进行测试:
#include <stdio.h>
int main()
{
printf("%d\n", 2.5);
return 0;
}
编译运行结果如下:
运行结果和我们预期的2不一样,使用gdb调试,在main函数处插入断点,并且反汇编main函数之后得到如图:
fldl addr 指令将内存addr中的双精度浮点数加载到FPU寄存器堆栈,fstpl value 将双精度数据从FPU寄存器堆栈出栈,保存到value中。因此,
0x08048415 <+9>: fldl 0x80484e0
0x0804841b <+15>: fstpl 0x4(%esp)
之后取出内存0x80484e0处的双精度浮点数加载到FPU寄存器st0中,再从st0中取出放到esp-4处。先使用gdb -x命令查看内存0x80484e0处的内容
(gdb) x/fg 0x80484e0
0x80484e0: 2.5
(gdb) x/2xw 0x80484e0
0x80484e0: 0x00000000 0x40040000
(gdb) x/8tb 0x80484e0
0x80484e0: 00000000 00000000 00000000 00000000 00000000 00000000 00000100 01000000
可以看到,以双字的小数查看结果为2.5,由于我们平台采用的是小端格式存储(little-edian,低位字节存储在低内存位置),所以将以字节查看得到的结果恢复成下面的表示方法:
01000000 00000100 00000000 00000000 00000000 00000000 00000000 00000000
我们用IEEE754标准的双精度格式解析上面这段二进制,符号位为0,即为正;指数位为10000000000(1024)减去偏移量1023为1;尾数0100…000,加上隐藏位1,为1.01(即十进制1.25)。所以结果为+1.25×21 = 2.5,符合我们的预期。
那么fstpl指令将该浮点数加载到esp-4处作为printf函数的参数,再接着指令“movl $0x80484d8,(%esp) ”将输出格式控制符"%d" 的指针保存到esp指向的位置作为printf函数的函数,我们可以使用gdb查看内存0x80484d8处是不是格式控制符字符串:
(gdb) x/4cb 0x80484d8
0x80484d8: 37 '%' 100 'd' 10 '\n' 0 '\000'
故现在在调用printf之前函数堆栈的结构如下所示:
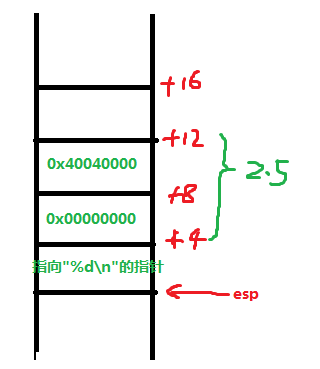
进入printf函数,解析第一个参数输出格式控制字符串,遇到%d,函数从之前压栈的参数取出一个整型即取到上图中esp+4处的值,以整型数输出,为0。这就是我们上面运行./test 的输出结果,而不是我想当然的程序会将2.5强制类型转化为整型得到2!
课本上习题答案:
2.58
/********2.58*********/
bool is_little_endian()
{
unsigned int x = 1;
return *((unsigned char*)&x);
}
2.59
(x & 0xFF) | (y & (~0xFF))
/****
*测试程序
****/
void test()
{
int x = 0x89ABCDEF;
int y = 0x76543210;
printf("%x\n",(x & 0xFF) | (y & (~0xFF)));
}
2.60
分析:先将第i个字节清空,再将该字节置为要求的字节
要定位到所给定的字的第i个字节,需要移动的位数为8*i,及i << 3,以下给出函数
/*********2.60**********/
unsigned replace_byte(unsigned x,unsigned char b,int i)
{
int shift = i << 3;
return (x & ~(0xff << shift)) | (b << shift);
}
2.61
每种情况为真对应一个表达式
- A. !(~x)
- B. !x
- C. x >>((sizeof(int) - 1) << 3) == -1
- D. !(x & (0xff))
2.62
分析:判断x移位之后是否还是全为1
bool int_shifts_are_logical()
{
int x = ~0x00;
x >>= 1;
return ~x;
}
2.63
int sra(int x,int k)
{
/* Perform shift logically*/
int xsrl = (unsigned) x >> k;
int w = 8 * sizeof(int);
bool flag = (1 << (w - 1)) & x;
flag && (xsrl | ((1 << k) - 1) << (w - k));
return xsrl;
}
分析:把前面的位都置为0即可
unsigned srl(unsigned x, int k)
{
/*Perform shift arithmetically*/
unsigned xsra = (int) x >> k;
int w = 8 * sizeof(int);
k && (xsra &= ((1 << (w - k)) - 1));
return xsra;
}
2.64
/*********2.64*********/
/*Return 1 when any even bit of x equals 1;0 otherwise Assume w=32*/
int any_even_one(unsigned x)
{
return (x & 0xaaaaaaaa) == 0xaaaaaaaa;
}
2.65
int even_ones(unsigned x)
{
x ^= x >> 1;
x ^= x >> 2;
x ^= x >> 4;
x ^= x >> 8;
x ^= x >> 16;
return x & 1;
}
巧妙的通过异或操作判断两位,四位,八位,十六位,最后到三十二位有偶数个1
2.66
根据题目提示先将x转换成00...011...11的格式再进行操作
/**********2.66**************/
int leftmost_one(unsigned x)
{
x |= x >> 1;
x |= x >> 2;
x |= x >> 4;
x |= x >> 8;
x |= x >> 16;
return x ^ (x >> 1);
}
2.67
A. 当移位数过大时,有的编译器会进行取模操作,有的则不会,故代码不是通用的
B.
int int_size_is_32()
{
<span style="white-space:pre"> </span>int set_msb = 1 << 31;
<span style="white-space:pre"> </span>int beyond_msb = 1 << 32;
<span style="white-space:pre"> </span>return set_msb && !(beyond_msb & ~(0x01));
}
C.
int int_size_is_32()
{
<span style="white-space:pre"> </span>int set_msb = 1 << 15;
<span style="white-space:pre"> </span>int beyond_msb = 1 << 32;
<span style="white-space:pre"> </span>return set_msb && !(beyond_msb & ~(0x01));
}
2.58
/********2.58*********/
bool is_little_endian()
{
unsigned int x = 1;
return *((unsigned char*)&x);
}
2.59
(x & 0xFF) | (y & (~0xFF))
/****
*测试程序
****/
void test()
{
int x = 0x89ABCDEF;
int y = 0x76543210;
printf("%x\n",(x & 0xFF) | (y & (~0xFF)));
}
2.60
分析:先将第i个字节清空,再将该字节置为要求的字节
要定位到所给定的字的第i个字节,需要移动的位数为8*i,及i << 3,以下给出函数
/*********2.60**********/
unsigned replace_byte(unsigned x,unsigned char b,int i)
{
int shift = i << 3;
return (x & ~(0xff << shift)) | (b << shift);
}
2.61
每种情况为真对应一个表达式
- A. !(~x)
- B. !x
- C. x >>((sizeof(int) - 1) << 3) == -1
- D. !(x & (0xff))
2.62
分析:判断x移位之后是否还是全为1
bool int_shifts_are_logical()
{
int x = ~0x00;
x >>= 1;
return ~x;
}
2.63
int sra(int x,int k)
{
/* Perform shift logically*/
int xsrl = (unsigned) x >> k;
int w = 8 * sizeof(int);
bool flag = (1 << (w - 1)) & x;
flag && (xsrl | ((1 << k) - 1) << (w - k));
return xsrl;
}
分析:把前面的位都置为0即可
unsigned srl(unsigned x, int k)
{
/*Perform shift arithmetically*/
unsigned xsra = (int) x >> k;
int w = 8 * sizeof(int);
k && (xsra &= ((1 << (w - k)) - 1));
return xsra;
}
2.64
/*********2.64*********/
/*Return 1 when any even bit of x equals 1;0 otherwise Assume w=32*/
int any_even_one(unsigned x)
{
return (x & 0xaaaaaaaa) == 0xaaaaaaaa;
}
2.65
int even_ones(unsigned x)
{
x ^= x >> 1;
x ^= x >> 2;
x ^= x >> 4;
x ^= x >> 8;
x ^= x >> 16;
return x & 1;
}
巧妙的通过异或操作判断两位,四位,八位,十六位,最后到三十二位有偶数个1
2.66
根据题目提示先将x转换成00...011...11的格式再进行操作
/**********2.66**************/
int leftmost_one(unsigned x)
{
x |= x >> 1;
x |= x >> 2;
x |= x >> 4;
x |= x >> 8;
x |= x >> 16;
return x ^ (x >> 1);
}
2.67
A. 当移位数过大时,有的编译器会进行取模操作,有的则不会,故代码不是通用的
B.
int int_size_is_32()
{
<span style="white-space:pre"> </span>int set_msb = 1 << 31;
<span style="white-space:pre"> </span>int beyond_msb = 1 << 32;
<span style="white-space:pre"> </span>return set_msb && !(beyond_msb & ~(0x01));
}
C.
int int_size_is_32()
{
<span style="white-space:pre"> </span>int set_msb = 1 << 15;
<span style="white-space:pre"> </span>int beyond_msb = 1 << 32;
<span style="white-space:pre"> </span>return set_msb && !(beyond_msb & ~(0x01));
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号