广度优先遍历和深度优先遍历

1 广度优先遍历

1.1 概念

①以初始节点V0作为第一层节点,接着访问它。
②然后迭代第一层节点即V0，访问它相邻接的没有访问过的节点比如V1,V2，V1,V2加入到第二层节点
③迭代第二层节点V1,V2，V1,V2依次访问相邻接的没有访问过的节点，重复上述步骤直至所有节点都被访问过为止。

1.2图解

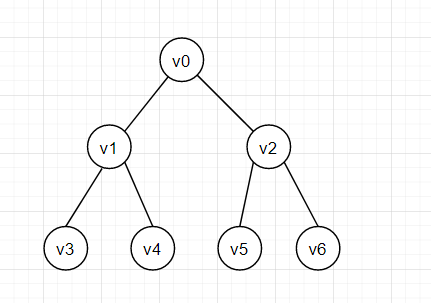
如图所示首先访问根节点v0,并将v0加入到第一层。迭代第一层节点，和vo相邻接的没有访问过的节点有v1和v2,访问v1和v2,并将v1和v2加入到第二层，迭代第二层中的节点v1和v2,和v1相邻接的没有访问过的节点有v3,v4,访问v3和v4，并加入到第三层，和v2相邻接的没有访问过的节点有v5和v6,访问v5和v6，并加入到第三层。

1.3代码

public class BFSDemo {

    public void bfs(TreeNode root) {
        if(root == null) {
            return;
        }
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        int size = q.size();
        TreeNode temp = null;
        while(!q.isEmpty()){
            size = q.size();
            while(size>0){
                temp = q.poll();
                if(temp.left != null){
                    q.offer(temp.left);
                }
                if(temp.right != null){
                    q.offer(temp.right);
                }
                size--;
            }
           
        }
        return;
    }

2.深度优先遍历

2.1概念

①从给定的一个节点v0作为起点，访问它。
②以v0作为起点，找到一个和它相邻且未被访问过节点v1,重复上述步骤。
③当到达一个节点vi，它所有相邻的节点都被访问过，那么就回退到vi-1,去找和它相邻且未被访问过节点。重复这一步，直到访问过的顶点在也找不到和它相邻且未被访问过的节点。

2.2图解

①v0->v1->v3
②回退到v1，->v3
③回退到v0, ->v2->v5
④回退到v2, ->v6

2.3代码

public class DFSDemo {

    public void dfs(TreeNode root) {
        if(root == null ) {
            return;
        }
        dfs(root.left);
        dfs(root.right);
        return;
    }
}

3例题

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]
返回它的最大深度 3 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

3.1分析

可以采用广度优先遍历，第一层深度为1，每增加一层深度加一
也可以采用深度优先遍历，访问每个节点时判断它和最大深度之间的大小。或者计算左子树深度和右子树的深度，取他们之间的最大值然后加1。

public class BFSDemo {

    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        int size = q.size();
        TreeNode temp = null;
        int level = 0;
        while(!q.isEmpty()){
            size = q.size();
            while(size>0){
                temp = q.poll();
                if(temp.left != null){
                    q.offer(temp.left);
                }
                if(temp.right != null){
                    q.offer(temp.right);
                }
                size--;
            }
            level++;
        }
        return level;
    }
}

public class DFSDemo {

    int max = 0;
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }

        dfs(root,1);
        return max;
    }
    public void dfs(TreeNode node, int level){
        if(node.left == null && node.right == null&&level>max){
            max = level;
        }
        if(node.left != null){
            dfs(node.left,level+1);
        }
        if(node.right != null){
            dfs(node.right,level+1);
        }
    }
}

public class DFSDemo {

    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left,right) + 1;
    }
}