Python实现高级的排序算法

分治法与归并排序

分治法 (Divide and Conquer)

很多有用的算法结构上是递归的，为了解决一个特定问题，算法一次或者多次递归调用其自身以解决若干子问题。 这些算法典型地遵循分治法的思想：将原问题分解为几个规模较小但是类似于原问题的子问题，递归求解这些子问题， 然后再合并这些问题的解来建立原问题的解。

分治法在每层递归时有三个步骤：

• 分解原问题为若干子问题，这些子问题是原问题的规模最小的实例
• 解决这些子问题，递归地求解这些子问题。当子问题的规模足够小，就可以直接求解
• 合并这些子问题的解成原问题的解

归并排序

归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

将数组分解最小之后，然后合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

归并排序分析

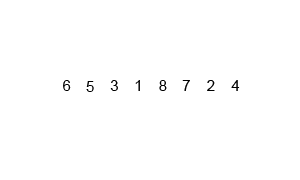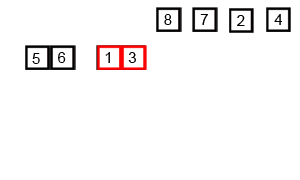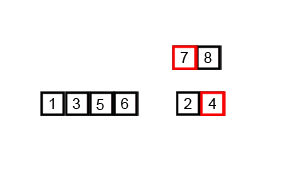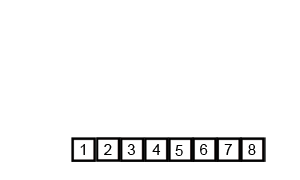
代码

# coding:utf-8
def merge_sort(alist):
    """归并排序"""
    n = len(alist)
    if n <= 1:
        return alist
    mid = n//2

    # left 采用归并排序后形成的有序的新的列表
    left_li = merge_sort(alist[:mid])

    # right 采用归并排序后形成的有序的新的列表
    right_li = merge_sort(alist[mid:])

    # 将两个有序的子序列合并为一个新的整体
    # merge(left, right)
    left_pointer, right_pointer = 0, 0
    result = []

    while left_pointer < len(left_li) and right_pointer < len(right_li):
        if left_li[left_pointer] <=  right_li[right_pointer]:
            result.append(left_li[left_pointer])
            left_pointer += 1
        else:
            result.append(right_li[right_pointer])
            right_pointer += 1

    result += left_li[left_pointer:]
    result += right_li[right_pointer:]
    return result


if __name__ == "__main__":
    li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print(li)
    sorted_li = merge_sort(li)
    print(li)
    print(sorted_li)

时间复杂度

• 最优时间复杂度：O(nlogn)
• 最坏时间复杂度：O(nlogn)
• 稳定性：稳定

快速排序

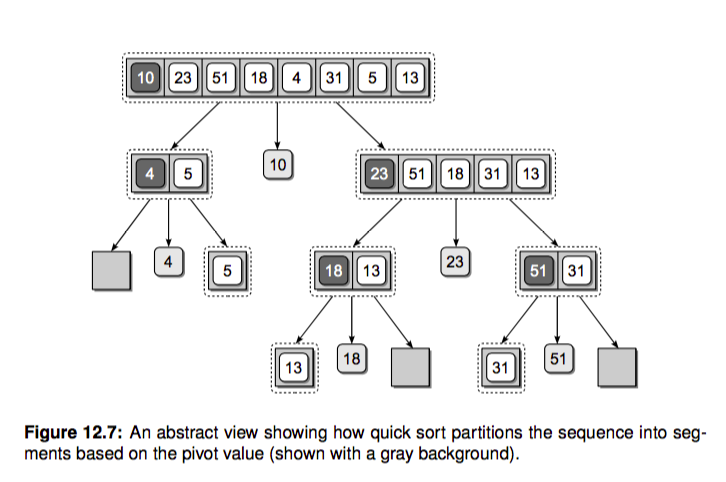
和归并排序一样，快排也是一种分而治之(divide and conquer)的策略。归并排序把数组递归成只有单个元素的数组，之后再不断两两 合并，最后得到一个有序数组。这里的递归基本条件就是只包含一个元素的数组，当数组只包含一个元素的时候，我们可以认为它本来就是有序的（当然空数组也不用排序）。

快排的工作过程其实比较简单，三步走：

• 选择基准值 pivot 将数组分成两个子数组：小于基准值的元素和大于基准值的元素。这个过程称之为 partition

• 对这两个子数组进行快速排序。

• 合并结果

 

 代码

# coding:utf-8


def quick_sort(alist, first, last):
    """快速排序"""
    if first >= last:
        return
    mid_value = alist[first]
    low = first
    high = last
    while low < high:
        # high 左移
        while low < high and alist[high] >= mid_value:
            high -= 1
        alist[low] = alist[high]

        while low <high and alist[low] < mid_value:
            low += 1
        alist[high] = alist[low]
    # 从循环退出时，low==high
    alist[low] = mid_value
    # 对low左边的列表执行快速排序
    quick_sort(alist, first, low-1)
    # 对low右边的列表排序
    quick_sort(alist, low+1, last)


if __name__ == "__main__":
    li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print(li)
    quick_sort(li, 0, len(li)-1)
    print(li)

快速排序进阶参考

关于快速排序进阶讲解可以参考这篇文章：快速排序