Python实现二分查找（递归与非递归2种方式）

递归的方式之前这篇博客也总结了：(递归应用)二分法查找数字

二分查找

二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

 

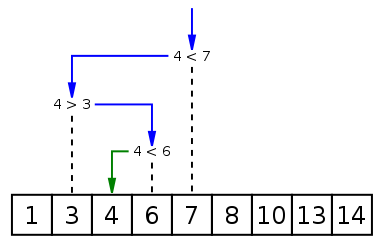
代码：

# coding:utf-8


def binary_search(alist, item):
    """二分查找,递归"""
    n = len(alist)
    if n > 0:
        mid = n//2
        if alist[mid] == item:
            return True
        elif item < alist[mid]:
            return binary_search(alist[:mid], item)
        else:
            return binary_search(alist[mid+1:], item)
    return False


def binary_search_2(alist, item):
    """二分查找， 非递归"""
    n = len(alist)
    first = 0
    last = n-1
    while first <= last:
        mid = (first + last)//2
        if alist[mid] == item:
            return True
        elif item < alist[mid]:
            last = mid - 1
        else:
            first = mid + 1
    return False


if __name__ == "__main__":
    li = [17, 20, 26, 31, 44, 54, 55, 77, 93]
    print(binary_search(li, 55))
    print(binary_search(li, 100))
    print(binary_search_2(li, 55))
    print(binary_search_2(li, 100))

时间复杂度

• 最优时间复杂度：O(1)
• 最坏时间复杂度：O(logn)