Python实现基本的排序算法
冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序算法的运作如下:
- 比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
时间复杂度
- 最优时间复杂度:O(n) (表示遍历一次发现没有任何可以交换的元素,排序结束。)
- 最坏时间复杂度:O(n2)
- 稳定性:稳定
代码
基础版本

# coding:utf-8 #从小到大排序 def bubble_sort(lis): for i in range(0,len(lis)): for j in range(1,len(lis)): if lis[j-1] > lis[j]: lis[j-1],lis[j] = lis[j],lis[j-1] if __name__ == '__main__': l1 = [2, 43, 22, 56, 13, 1, 9, 11, 32, 90] l2 = [3, 12, 6, 123, 11, 91, 45, 22, 67, 98] bubble_sort(l1) bubble_sort(l2) print(l1) print(l2)
优化

#coding:utf-8 #如果我们能判断出数列已经有序,并且做出标记,剩下的几轮排序就可以不必执行,提早结束工作。 def bubble_sort(lis): for i in range(0,len(lis)): # 是否进行数据交换的标记,每一轮循环起始值都是True is_sorted = True for j in range(1,len(lis)): if lis[j-1] > lis[j]: lis[j-1],lis[j] = lis[j],lis[j-1] is_sorted = False # 每一轮循环完判断下,如果发生了数据交换表示进行了排序 # 如果没有发生数据交换表示数据其实已经拍好了 if is_sorted == True: break if __name__ == '__main__': l1 = [2, 43, 22, 56, 13, 1, 9, 11, 32, 90] l2 = [3, 12, 6, 123, 11, 91, 45, 22, 67, 98] bubble_sort(l1) bubble_sort(l2) print(l1) print(l2)
继续优化

#coding:utf-8 #在每一轮排序的最后,记录下最后一次元素交换的位置,那个位置也就是无序数列的边界,再往后就是有序区了。 def bubble_sort(lis): # 最后一次交换的位置 last_sort_index = 0 # 无序区与有序区的边界 sort_border = len(lis) for i in range(0,len(lis)): # 每一轮循环之前设置是否发生数据交换的标志 # 是否发生了数据交换,初始值为True is_sorted = True # “小循环”比较的话以sort_border作为分界 for j in range(1,sort_border): if lis[j-1] > lis[j]: lis[j-1],lis[j] = lis[j],lis[j-1] # 发生了数据交换,标志值设置为False is_sorted = False # 记录最后一次交换的位置 last_sort_index = j # 在“大循环”外记录无序区与有序区的边界、 # 就是最后一个j的值,被last_sort_index拿到了 sort_border = last_sort_index # 如果没有发生数据交换,直接跳出大循环 if is_sorted: break if __name__ == '__main__': l1 = [2, 43, 22, 56, 13, 1, 9, 11, 32, 90] l2 = [3, 12, 6, 123, 11, 91, 45, 22, 67, 98] bubble_sort(l1) bubble_sort(l2) print(l1) print(l2)
升级:鸡尾酒排序原始版

# coding:utf-8 # 排序过程就像钟摆一样,第一轮从左到右,第二轮从右到左,第三轮再从左到右...... def cock_tail_ort(lis): for i in range(0,len(lis)): # 数据交换的标志 is_sorted = True ## 从左至右冒泡 for j in range(1,len(lis)): if lis[j-1] > lis[j]: lis[j-1],lis[j] = lis[j],lis[j-1] is_sorted = False if is_sorted: break ## 从右至左冒泡、 # 重新设置下数据交换的标志 is_sorted = True # 反向遍历 注意这里结束的标志是i # 而且j是从大到小的 for j in range(len(lis)-1,i,-1): if lis[j-1] > lis[j]: lis[j-1],lis[j] = lis[j],lis[j-1] is_sorted = False if is_sorted: break if __name__ == '__main__': l1 = [2, 43, 22, 56, 13, 1, 9, 11, 32, 90] l2 = [3, 12, 6, 123, 11, 91, 45, 22, 67, 98] cock_tail_ort(l1) cock_tail_ort(l2) print(l1) print(l2)
鸡尾酒排序升级版

# 我们可以在每一轮排序的最后,记录下最后一次元素交换的位置,那个位置也就是无序数列的边界,再往后就是有序区了。 # 对于单向的冒泡排序,我们需要设置一个边界值,对于双向的鸡尾酒排序,我们需要设置两个边界值。 # 整个过程分为“正序”与“倒序”,正序是从左至右遍历冒泡,倒序是从右至左遍历冒泡 def chicken_tail_sort(lis): # 从左至右最后一次数据交换的位置 以及 右边界 left_last_exchange_index = 0 right_border = len(lis)-1 # 从右至左最后一次数据交换的位置 以及 左边界 right_last_exchange_index = 0 left_border = 0 # 开始遍历 其实这里大循环一半就OK了 for i in range(0,len(lis)//2): # 设置数据交换标志 is_sorted = True # 从左至右遍历,以右边界作为终点 注意这里range是左闭右开区间,结尾得+socketserver模块-循环接收0 for j in range(left_border,right_border+1): if lis[j-1] > lis[j]: lis[j-1],lis[j] = lis[j],lis[j-1] is_sorted = False # 更新最后一次数据交换的位置 right_last_exchange_index = j # 得出每一次轮训右边界的位置 right_border = right_last_exchange_index if is_sorted: break ## 开始从右往左遍历,记得设置下is_sorted is_sorted = True # 从右往左,从右边界到左边界 for j in range(right_border,left_border,-1): if lis[j-1] > lis[j]: lis[j-1],lis[j] = lis[j],lis[j-1] is_sorted = False #记录最后一次数据交换的位置 left_last_exchange_index = j # 得出左边界的位置 left_border = left_last_exchange_index if is_sorted: break if __name__ == '__main__': l1 = [2, 43, 22, 56, 13, 1, 9, 11, 32, 90,23,112,445,1213,12,45,89,32] l2 = [3, 12, 6, 123, 11, 91, 45, 22, 67, 98] chicken_tail_sort(l1) chicken_tail_sort(l2) print(l1) print(l2)
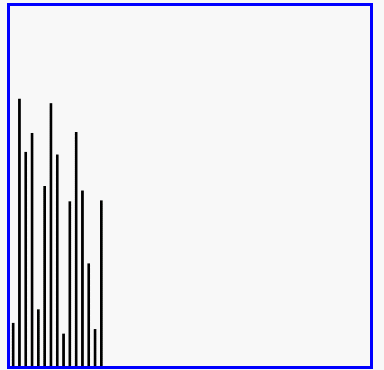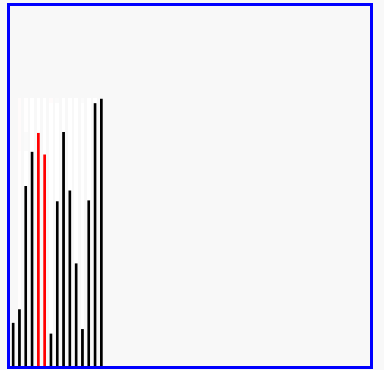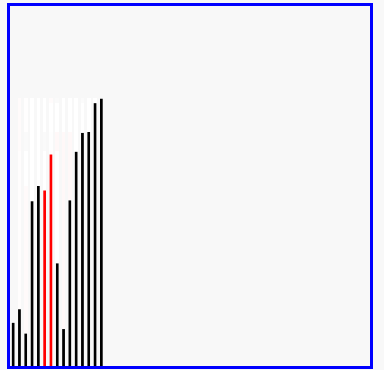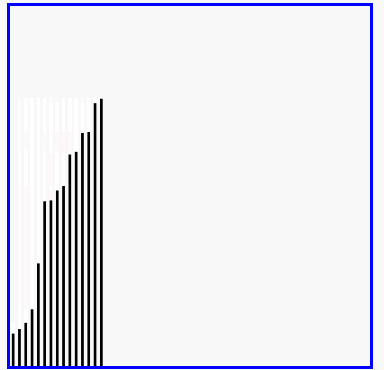
冒泡排序的效果演示
插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
插入排序分析
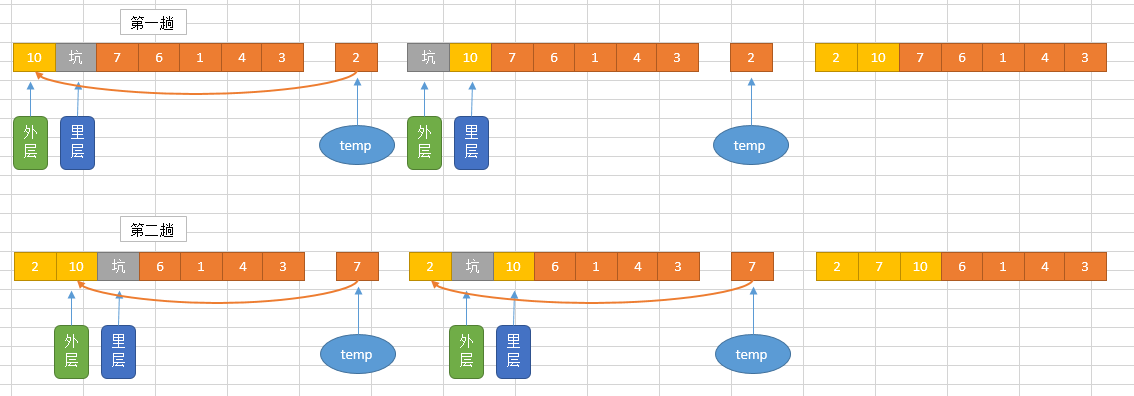
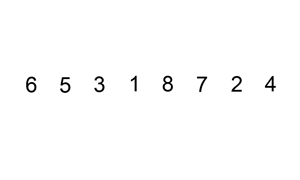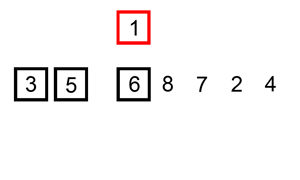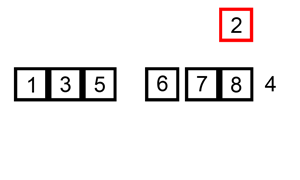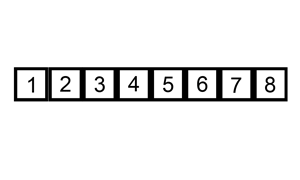
时间复杂度
- 最优时间复杂度:O(n) (升序排列,序列已经处于升序状态)
- 最坏时间复杂度:O(n2)
- 稳定性:稳定
代码
# coding:utf-8 def insert_sort(alist): """插入排序""" n = len(alist) # 从右边的无序序列中取出多少个元素执行这样的过程 for j in range(1, n): # j = [1, 2, 3, n-1] # i 代表内层循环起始值 i = j # 执行从右边的无序序列中取出第一个元素,即i位置的元素,然后将其插入到前面的正确位置中 while i > 0: if alist[i] < alist[i-1]: alist[i], alist[i-1] = alist[i-1], alist[i] i -= 1 else: break if __name__ == "__main__": li = [54, 26, 93, 17, 77, 31, 44, 55, 20] print(li) insert_sort(li) print(li)
插入排序效果演示

希尔排序
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
希尔排序过程
希尔排序的基本思想是:将数组列在一个表中并对列分别进行插入排序,重复这过程,不过每次用更长的列(步长更长了,列数更少了)来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法,算法本身还是使用数组进行排序。
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样(竖着的元素是步长组成):
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
然后我们对每列进行排序:
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]。这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45
排序之后变为:
10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94
最后以1步长进行排序(此时就是简单的插入排序了)
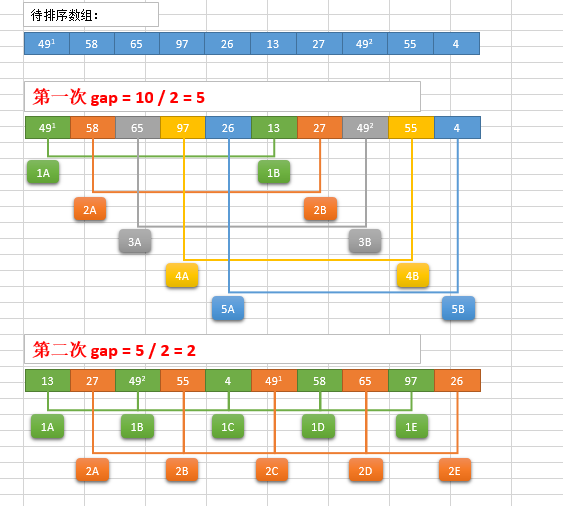
代码
# coding:utf-8 def shell_sort(alist): """希尔排序""" n = len(alist) gap = n // 2 # gap变化到0之前,插入算法执行的次数 while gap > 0: # 插入算法,与普通的插入算法的区别就是gap步长 for j in range(gap, n): i = j while i > 0: if alist[i] < alist[i-gap]: alist[i], alist[i-gap] = alist[i-gap], alist[i] i -= gap else: break # 缩短gap步长 gap //= 2 if __name__ == "__main__": li = [54, 26, 93, 17, 77, 31, 44, 55, 20] print(li) shell_sort(li) print(li)
时间复杂度
- 最优时间复杂度:根据步长序列的不同而不同
- 最坏时间复杂度:O(n2)
- 稳定性:不稳定
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。
选择排序分析
红色表示当前最小值,黄色表示已排序序列,蓝色表示当前位置。
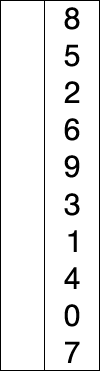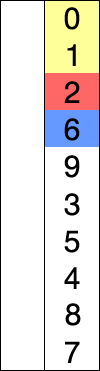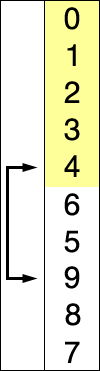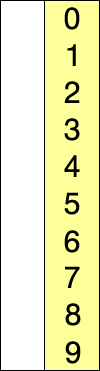
代码
def selection_sort(alist): n = len(alist) # 需要进行n-1次选择操作 for i in range(n-1): # 记录最小位置 min_index = i # 从i+1位置到末尾选择出最小数据 for j in range(i+1, n): if alist[j] < alist[min_index]: min_index = j # 如果选择出的数据不在正确位置,进行交换 if min_index != i: alist[i], alist[min_index] = alist[min_index], alist[i] alist = [54,226,93,17,77,31,44,55,20] selection_sort(alist) print(alist)
时间复杂度
- 最优时间复杂度:O(n2)
- 最坏时间复杂度:O(n2)
- 稳定性:不稳定(考虑升序每次选择最大的情况)
使用Python实现高级排序算法 ***
常见的算法效率比较
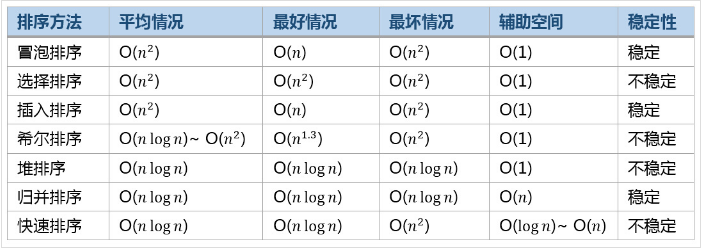



 浙公网安备 33010602011771号
浙公网安备 33010602011771号