机器学习工程师 - Udacity 强化学习 Part Eleven

十、行动者-评论者方法

1.行动者-评论者方法
我们可以通过两大类别的方法解决强化学习问题。对于蒙特卡罗学习或 Q 学习等基于值的方法，我们会尝试表示每个状态或状态动作对的值，然后，根据任何状态我们可以选择具有最佳值的动作。如果你有数量有限的动作，这种方法很合适。另一方面，基于策略的方法会对从状态到动作的映射进行编码，不用担心值表示法，然后尝试直接优化策略。当动作空间是连续性或者需要随机策略时，这种方法非常有用。基于策略的方法存在的最大挑战是很难计算策略到底有多好，这时候我们就要用到值函数这一概念。如果我们跟踪状态或状态动作值，并使用这些数据计算目标而不是根据奖励或回报计算策略目标，就是行动者-评论者方法。

2.更好的得分函数
回忆下典型策略梯度更新规则中使用的得分函数：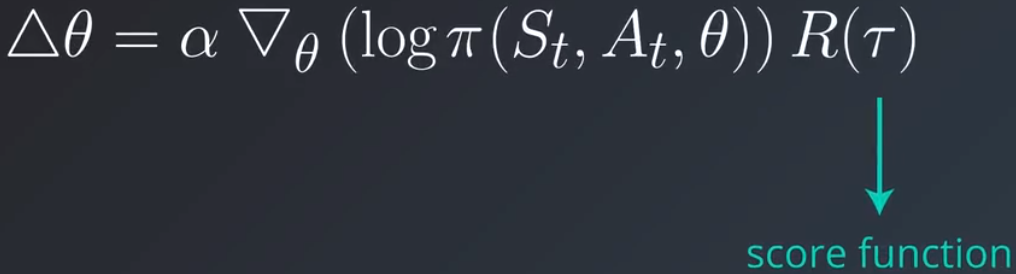

对于阶段性任务，每个实例有一个清晰的开始和结束点，你可以使用阶段回报 Gt 作为得分函数的值：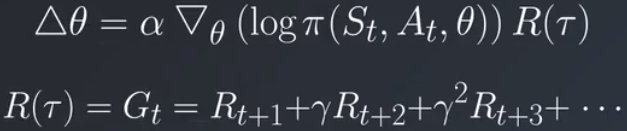

它等同于在该阶段后续时间内获得的所有奖励的折扣和。这就是蒙特卡洛方法的基础。例如在每个阶段结束时进行更新的强化算法。但是如果任务不是阶段性的该怎么办？如果没有清晰的结束点，则无法计算折扣回报。更糟糕的是，何时进行策略更新？很明显我们需要更好的得分函数，在与环境互动时能够在线计算的函数，并且不依赖于正在运行的整个阶段。我们将更新规则中的阶段替换为当前状态动作对的动作值，和我们在基于值的方法中尝试估算的动作值相同。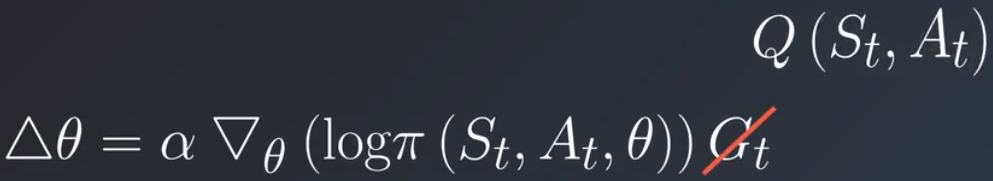

怎么找到这些动作值？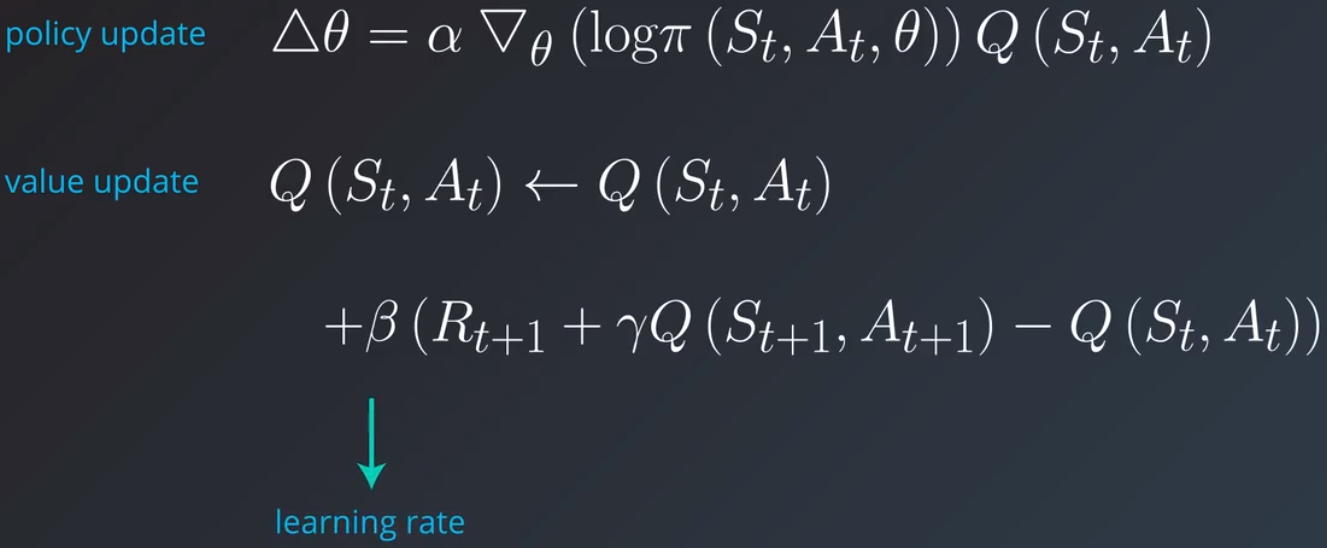

我们需要自己弄清楚这些值，除非有个预言者可以明确告诉这些值应该是多少。例如，我们可以使用时间差分机制迭代地更新这些动作值。注意，该流程可以与策略更新同步运行，不需要在整个阶段运行完毕后再执行。因此，可以用于非阶段性或连续性任务。实际上，你可以选择任何合适的表示法来存储这些 Q 值，然后使用合适的算法更新它们。注意，这里的 β 是另一个学习速率或步长参数，和 α 一样，但是针对的是值更新。

3.两个函数逼近器
对于大多数复杂的问题，你都需要处理连续状态和动作空间，我们通过 Q 学习和函数逼近来估算动作值。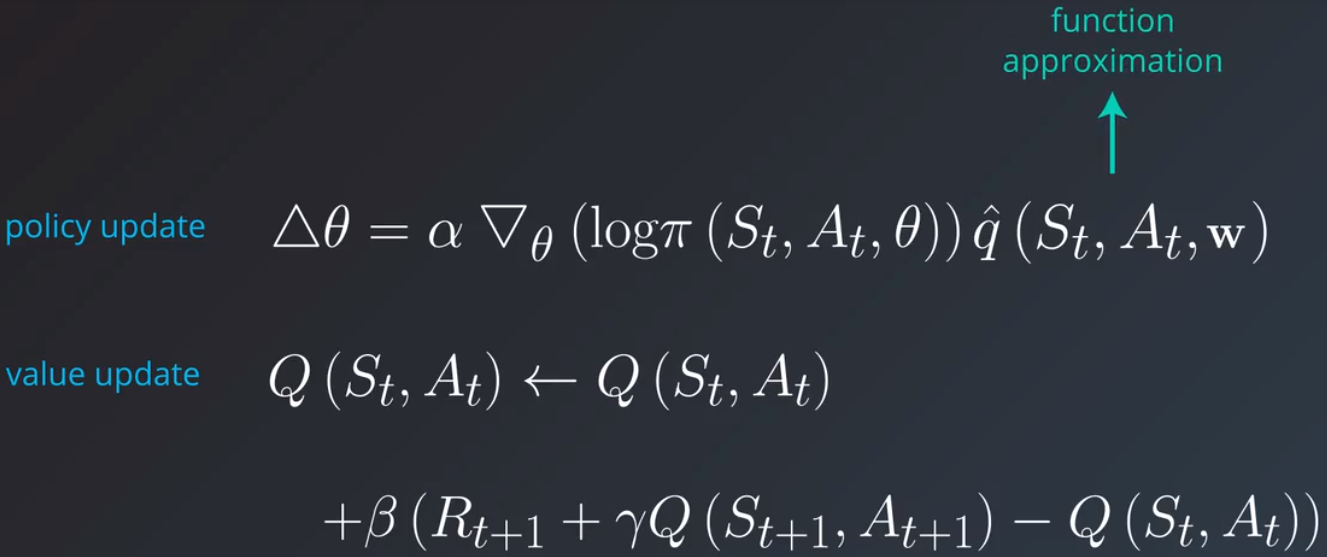

这是一个动作值函数的相应更新规则，表示为权重变化 Δw：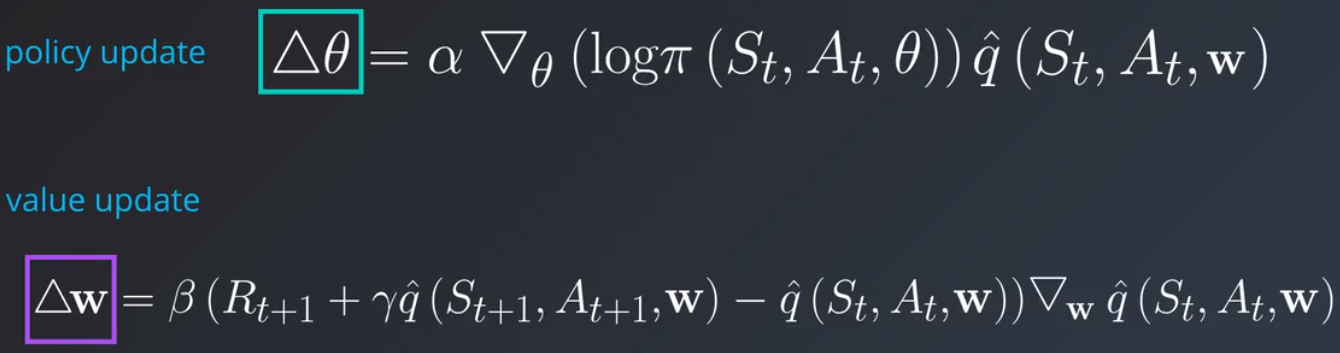

注意 θ 和 w 是不同的参数向量，但是它们很相似，分别表示一种函数逼近，θ 表示策略 π 在给定状态采取某个动作的概率，w 表示从该状态采取该动作的值 q^。我们先不管更新规则并重点看看这两个函数。π 控制强化学习智能体的行为或动作方式，可以将 π 看做在舞台上控制木偶表演的木偶师，q^ 衡量的是这些动作的效果，即对这些动作进行评价，这是两个函数逼近器，策略或行动者以及值或评论者，你可以单独设计它们，或许可以使用两个神经网络，并且可以使用单独的流程训练它们。

4.行动者和评论者
我们尝试开发一个完整的架构来训练行动者和评论者组件。思考下应该采用什么样的流程。一开始，行动者遵守的是某个随机的策略并且行为很糟糕，评论者观察该行为并提供反馈，告诉行动者行为有多糟糕，行动者根据该反馈更新策略 π 并再次行动，评论者继续提供更多反馈，评论者也会更新自己的备注或值函数以便提供更好的反馈。这一流程一直持续下去，直到行动者达到提前设定的性能阈值，或者没有什么改进。注意，与此同时评论者也会一直通过观察从环境中获得的状态和奖励，学习提供越来越好的反馈。现在我们已经完整地了解了不同组件之间的交互关系，我们重新介绍下每个组件背后的数学原理。策略逼近器 π 由 θ 参数化，值函数逼近器 q^ 由 w 参数化，在每个时间步 t 我们都从环境中抽样当前状态并表示为 S_t，策略用它作为输入，生成动作 A_t，行动者在环境中采取此动作生成下个状态 S_t+1 以及奖励 R_t+1。现在评论者使用值函数 q^ 计算在状态 S_t 采取动作 A 的值，行动者使用这个 q 值更新策略参数 θ，根据这些更新的参数，行动者生成下个动作 A_t+1。最后，评论者更新自己的值函数。在每个时间步都重复这一流程，而不仅仅是在阶段结束时，因此行动者和评论者都可以更有效地利用与环境的互动结果。

5.优势函数
我们仔细研究下我们的更新机制，看看是否有任何改进之处。

还记得这个策略更新规则来自何处吗？它基于策略梯度方法。我们以很小的分数 α，目标函数的梯度 jθ 更改策略参数，这个梯度可以表示为策略乘以某个得分函数 R 生成的对数概率的导数预期值。在此处，我们将动作值函数 q^ 作为得分函数。这个方法可行的原因是我们可以采取很小的步长（由学习速率 α 定义）迭代地计算该预期值。务必确保始终采取很小的步长。我们依然希望沿着梯度所指的方向移动，但是需要避免很大的步长，因为最终是抽样随机流程，单个样本可能会变化很大。只要是预期值，就存在相关的方差，如果我们尝试估算这个预期值，则最好样本之间的方差很小，这样使得该流程更加稳定。该方程的大小主要受到得分函数 q^ 的影响，在每个时间步，q^ 的值可能变化很大，因为它基于单个奖励，这样可能会导致策略更新步长不一，有时候是很小的步长，有时候是很大的步长，如何减小这一方差？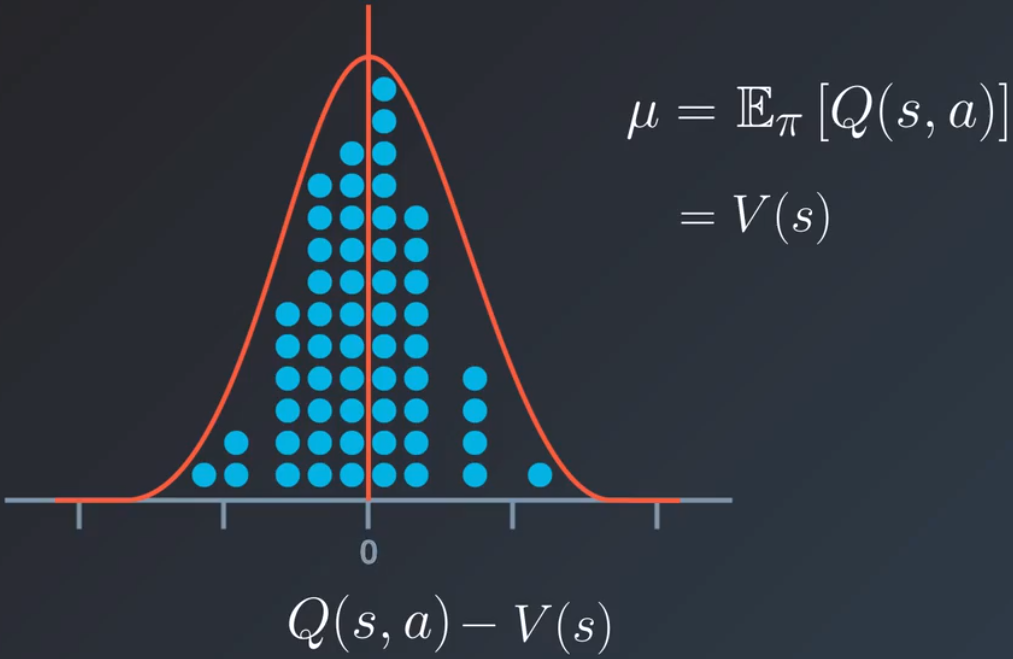

假设 q 值抽样自某个分布，假设这个分布是正态分布或高斯分布，能算出该分布的均值是什么吗？均值是 q^ 的预期值，对于特定的状态 s，这个分布针对的是动作空间，因此预期值本质上等于状态值。如果用每个 Q 值减去这个均值并用作新的得分函数，这样会使得均值得分值降低为 0，有助于减小更新步长的偏差，这个新得分函数称之为优势函数：

可以直观地看出它很合理。Q 值告诉我们在状态 s 采取动作 a，预期可以获得的奖励。优势函数告诉我们在状态的预期值之外我们预期会获得多少额外的奖励，即我们采取该动作（而不是任何随机的动作）会获得什么。优势函数不仅会稳定学习过程，而且可以更好地区分动作。

6.行动者-评论者方法与优势函数
优势函数对行动者-评论者算法有何影响？我们先从策略更新规则开始：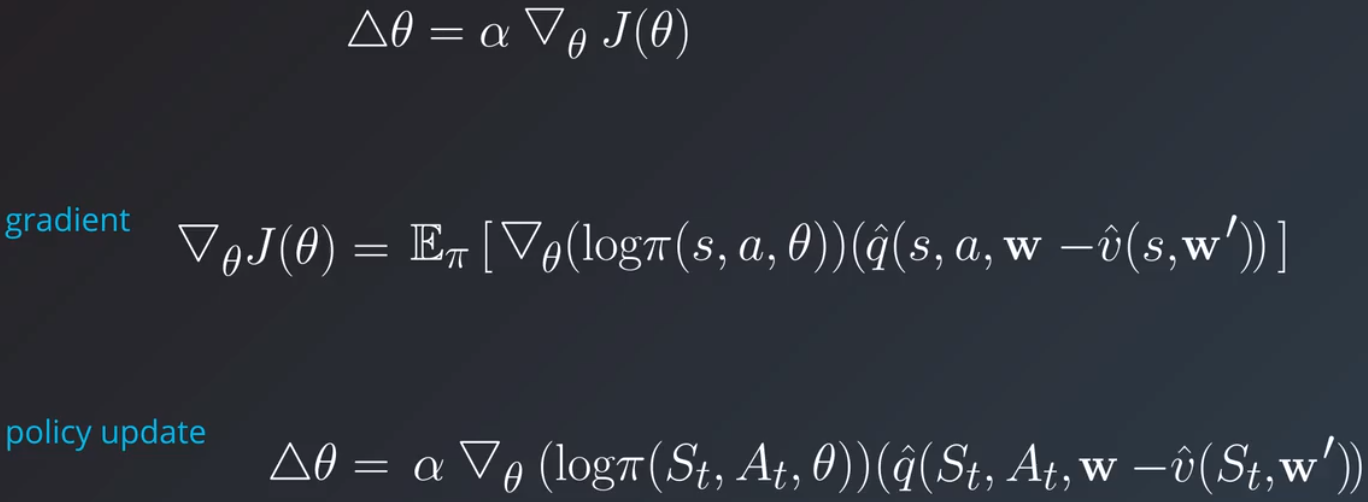

我们想用优势值替换这个状态动作值，最自然的方式是定义另一个状态值函数 v^，参数形式为 W′ 并用 q 值减去它，这意味着评论者现在需要跟踪两个值函数，Q^ 和 V^，并逐渐学习它们。还有更简单的方式：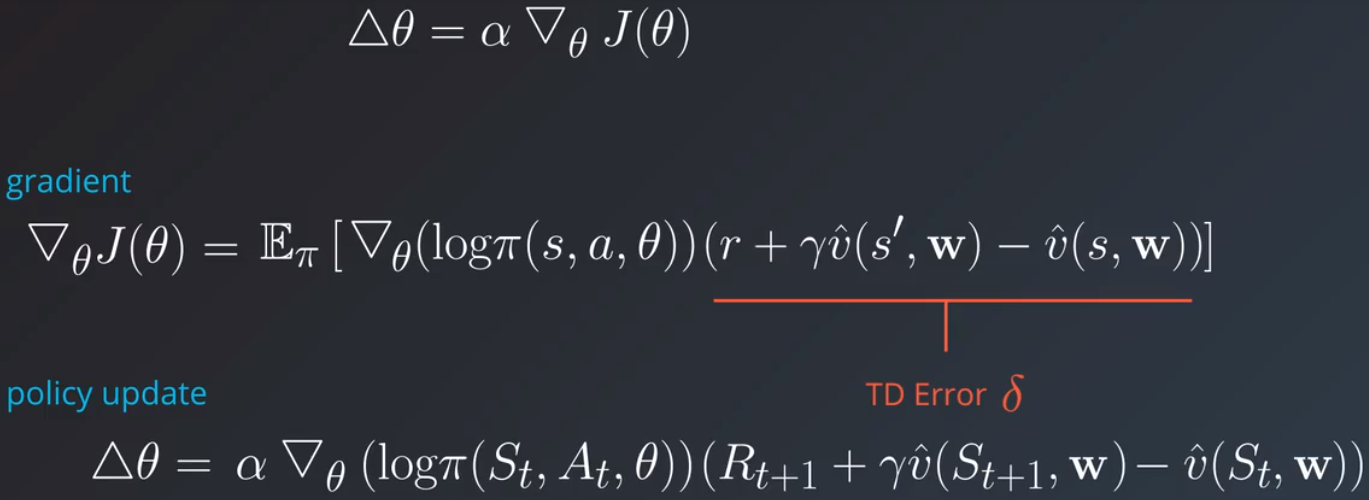

实际上 TD 误差 δ 可以很好地估算优势函数。使用该方法后，评论者现在只需计算并学习一个值函数 v^ 就行了。