机器学习工程师 - Udacity 强化学习 Part Five
六、时间差分方法
1.给定一个策略,如何估算其值函数?在蒙特卡洛方法中,智能体以阶段形式与环境互动,一个阶段结束后,我们按顺序查看每个状态动作对,如果是首次经历,则计算相应的回报并使用它来更新动作值。我们经历了很多很多个阶段。需要注意的是,只要我们不在阶段之间更改策略,该算法就可以解决预测问题,只要我们运行该算法足够长的时间,就肯定能够获得一个很完美的动作值函数估计结果:

2.现在将重点转移到这个更新步骤:
![]()
这行的主要原理是,任何状态的值定义为智能体遵守策略后在该状态之后很可能会出现的预期回报,对取样回报取平均值生成了很好的估值。回想下关于状态值的贝尔曼预期方程,它可以使用潜在地跟在后面的状态的值表示任何状态的值:
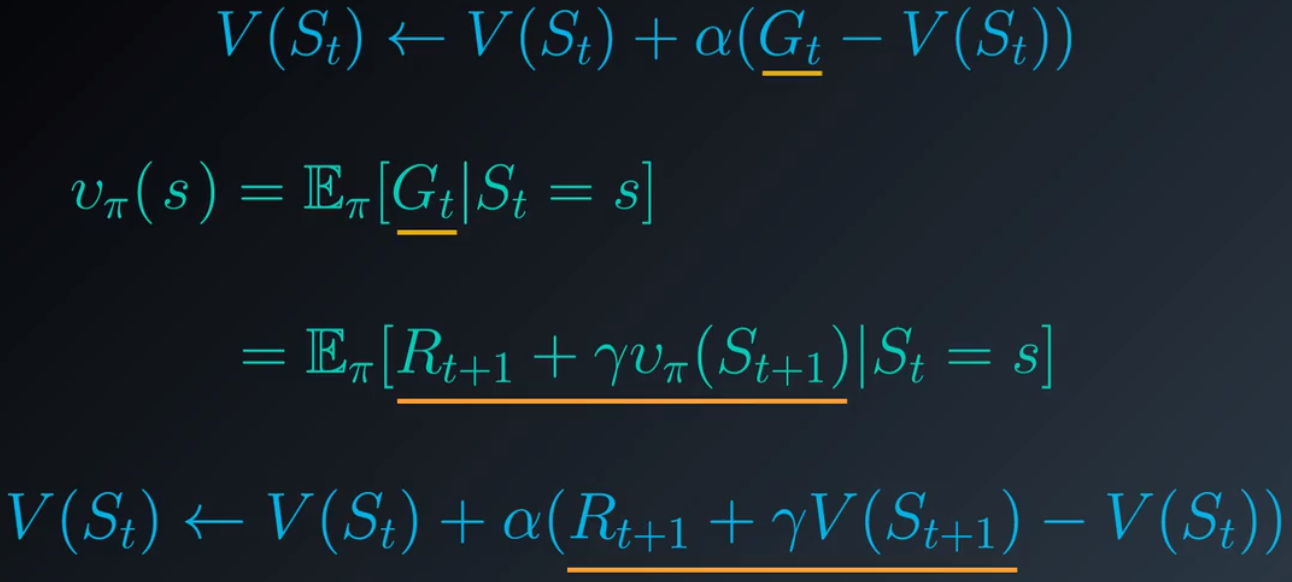
现在我们不再对取样回报取平均值,而是根据后续状态的值来估算,这就使得我们能够在每个时间步之后更新状态值。
3.改写上述方程式:
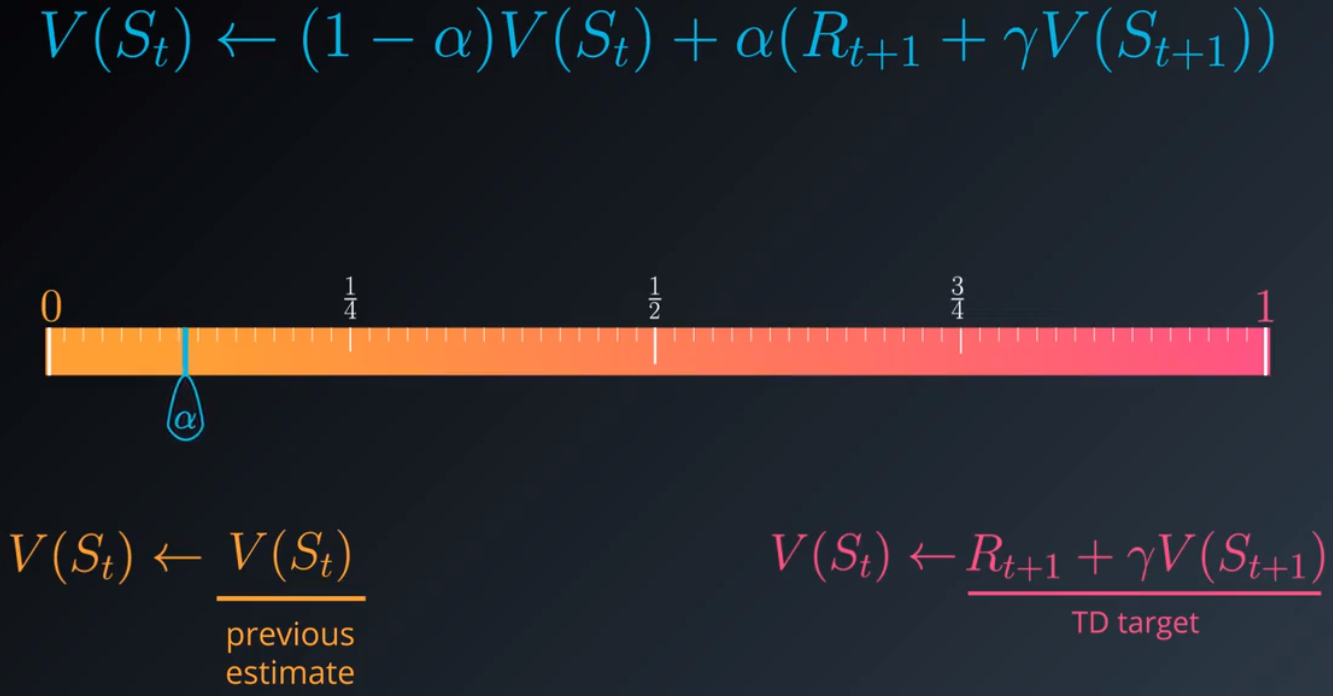
我们需要在当前估值和TD目标之间做一个平衡。α 必须设为 0 和 1 之间的某个数字。当 α 设为 1 时,新的估值是 TD 目标,我们完全忽略并替换之前的估值,如果将 α 设为 0,则完全忽略目标并保留旧的估值,我们肯定不希望出现这种结果,因为智能体将无法学到规律。将 α 设为一个接近 0 的小值很有帮助,通常 α 越小,我们在进行更新时对目标的信任就越低,并且更加依赖于状态值的现有估值。
4.TD算法的伪代码:

TD(0) 保证会收敛于真状态值函数,只要步长参数 α 足够小。MC 预测也是这种情况。但是,TD(0) 具有一些优势:
- MC 预测必须等到阶段结束时才能更新值函数估值,但是, TD 预测方法在每个时间步之后都会更新值函数。同样,TD 预测方法适合连续性和阶段性任务,而 MC 预测只能应用于阶段性任务。
- 在实践中,TD 预测的收敛速度比 MC 预测的快。(但是,没有人能够证明这一点,依然是一个需要验证的问题。)要获取了解如何运行此类分析的示例,请参阅该教科书的第 6.2 个示例。
在阶段性任务中使用TD(0),只需检查在每个时间步,最近的状态是否为最终状态,如果是,我们最后一次运行更新步骤以便更新上一个状态,然后开始一个新的阶段。
5.动作值
时间差分的原理是,智能体与环境互动,在时间步 0 收到状态 S0,然后根据策略选择一个动作,紧接着智能体收到奖励和下个状态,此刻,智能体根据经验更新时间步 0 时状态的估算值,在下个时间点,智能体通过查看策略再次选择一个动作,并收到奖励和下个状态,然后利用该信息更新时间步 1 时的状态的值。问题是,我们如何调整该流程,返回动作值的估值?我们不再使用与后续状态的值相关的更新方程,而是需要获得一个与后续状态动作对的值相关的更新方程,智能体将在每次选择动作后都更新值,而不是在接收每个状态后更新值。
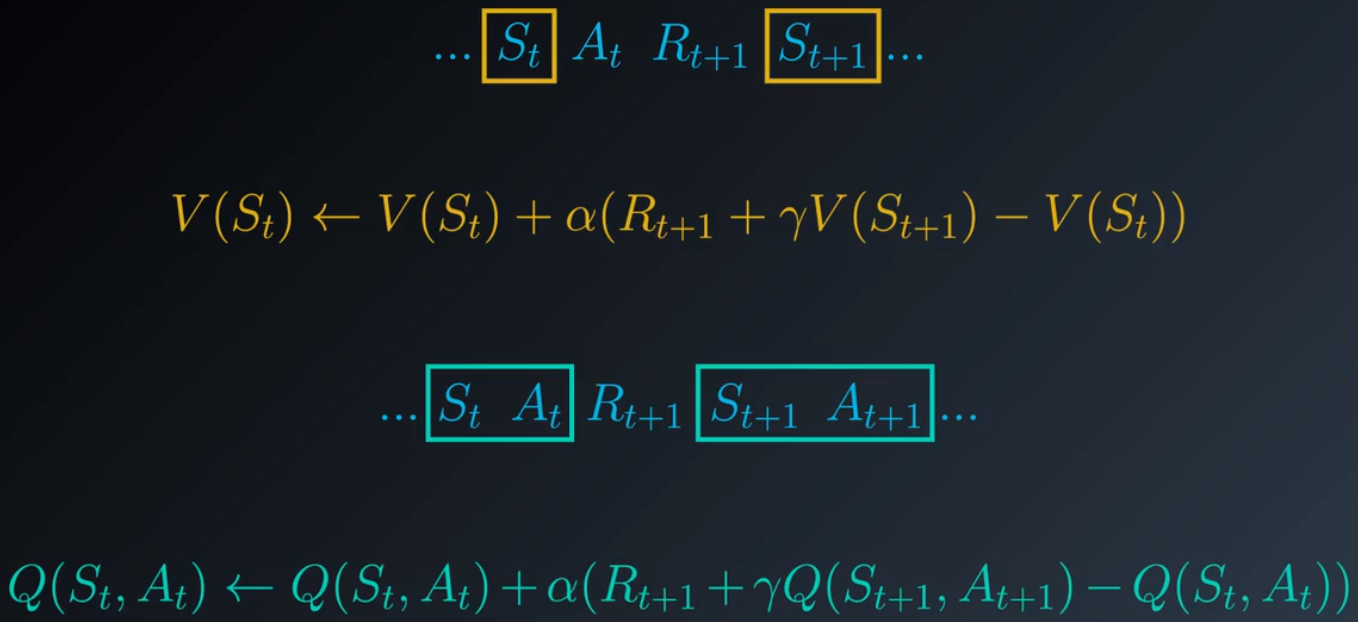
6.我们已经解决了预测问题,可以讨论控制问题了。智能体如何确定最优策略?我们将采用估算动作值函数的算法。在此算法中,选择每个动作后,智能体都更新估值,需要注意的是,智能体在每个时间步都使用相同的策略来选择动作。但是现在,为了调整该算法以便生成控制算法,我们将逐渐更改该策略,使其在每个时间步都越来越完善。我们将使用的方法与蒙特卡洛方法非常相似,即在每个时间步使用一个针对当前动作估值的 Epsilon 贪婪策略选择一个动作。在初始时间步,我们先将 ε 设为 1,然后根据对等概率随机策略选择 A0 和 A1。在选择某个动作之后的未来所有时间步,我们都更新动作值函数并构建相应的 Epsilon 贪婪策略,只要我们为 ε 指定合适的值,该算法就肯定会收敛于最优策略。该算法的名称叫做 Sarsa 0,简称为 Sarsa。得名原因是每个动作值更新都使用状态(S)动作(A)奖励(R)后续状态(S) 后续动作(A)。

7.Sarsa(0)

Sarsa(0) 保证会收敛于最优动作值函数,只要步长参数 α 足够小,并且满足有限状态下的无限探索贪婪算法 (GLIE) 条件。虽然有满足 GLIE 条件的很多方式,但是有一种方式在构建 ϵ 贪婪策略时会逐渐降低 ϵ 的值。
尤其是,使 ϵi 对应于第 i 个时间步。然后,如果我们按照以下条件设置 ϵi:
- 对于所有时间步 i,ϵi>0,以及
- 当时间步 i 接近无穷大时,ϵi 降低到 0
然后该算法会保证产生一个很好的 q∗ 估值,只要我们运行该算法足够长的时间。然后,可以通过对所有 s∈S 设置 π∗(s)=arg maxa∈A(s)q∗(s,a),获得相应的最优策略 π∗。
8.Sarsamax
对于 Sarsa 算法,我们先将所有动作值初始化为 0,并构建相应的 Epsilon 贪婪策略。然后,智能体开始与环境互动并接收第一个状态,接着,它使用该策略选择动作,紧接着,它收到一个奖励和下个状态,然后,智能体再次使用相同的策略选择下个动作,选择该动作后,它会更新对应于上个状态动作对的动作值,并根据最新的动作估值将该策略更新为 Epsilon 贪婪策略。Sarsamax亦称之为 Q 学习。我们依然采用相同的初始动作值和策略,智能体接收初始状态,依然根据初始策略选择第一个动作,但是在接收奖励和下个状态后我们将执行不同的操作,即我们将在选择下个动作之前更新策略。你能猜到这里适合采用什么样的动作吗?对于 Sarsa 算法,我们的更新步骤是晚一个步骤,并代入使用 Epsilon 贪婪策略选择的动作,对于该算法的每一步,我们更新动作值使用的所有动作都完全与智能体体验的动作一样。但是通常并非必须这样。尤其是,考虑使用贪婪策略的动作,而不是使用 Epsilon 贪婪策略的动作,这就是 Sarsamax 或 Q 学习的流程。

某个状态对应的贪婪动作正好是最大化该状态的动作值的动作。我们使用贪婪动作更新时间步 0 的动作值后使用刚刚更新的动作值对应的 Epsilon 贪婪策略选择 A1,当我们收到奖励和下个状态后继续这一流程,然后像之前使用贪婪动作更新 S1 和 A1 对应的动作一样使用相应的 Epsilon 贪婪策略选择 A2。在 Sarsa 中更新步骤使动作值更接近于智能体当前遵守 Epsilon 贪婪策略获得的动作值。可以显示 Sarsamax 直接在每个时间步估算最优值函数。

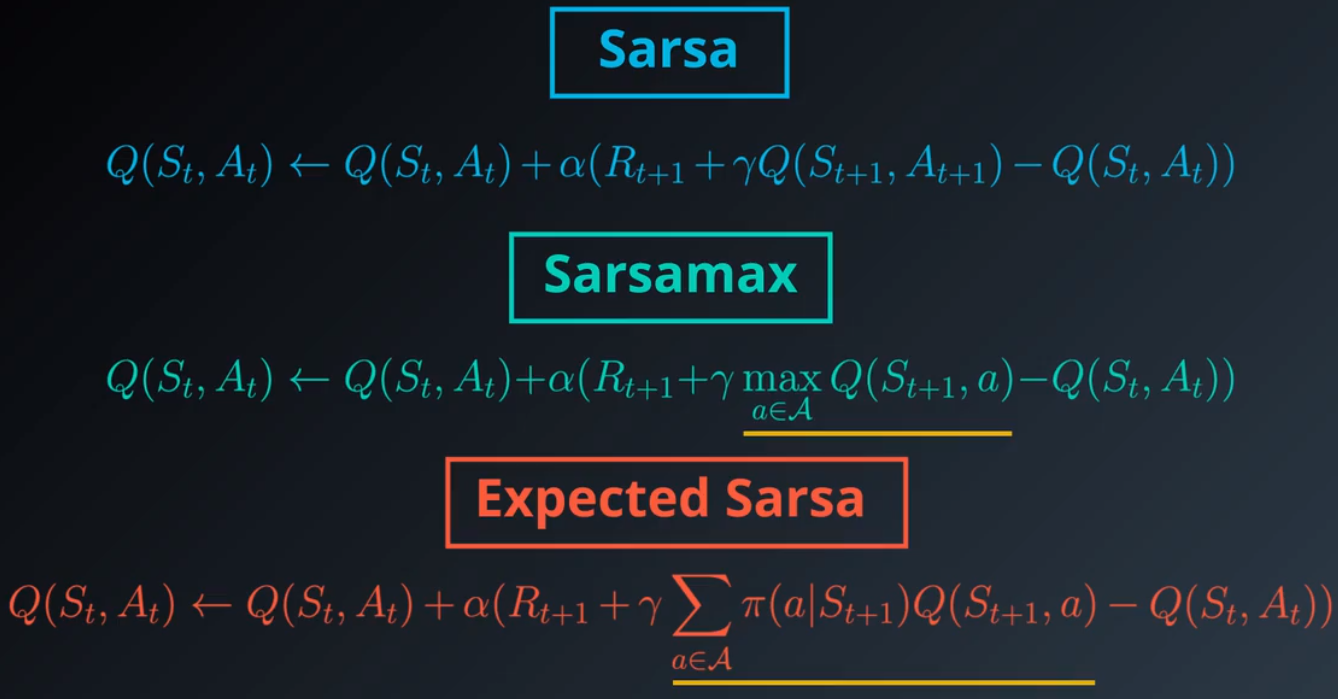
9.预期 Sarsa
预期 Sarsa 和 Sarsamax 非常相似,唯一区别是动作值的更新步骤。Sarsamax 或 Q 学习对所有可能的下个状态动作对都取最大动作,换句话说,它通过代入最大化下个状态对应的动作估值选择在此处采取的值。预期 Sarsa 有所不同,它使用下个状态动作对的预期值。预期值会考虑智能体从下个状态选择每个可能的动作的概率。

10.分析性能
在以下情况下,我们讨论过的所有 TD 控制算法(Sarsa、Sarsamax、预期 Sarsa)都会收敛于最优动作值函数 q∗(并生成最优策略 π∗):(1)ϵ 的值根据 GLIE 条件逐渐降低,以及 (2) 步长参数 α 足够小。
这些算法之间的区别总结如下:
- Sarsa 和预期 Sarsa 都是异同策略 TD 控制算法。在这种情况下,我们会根据要评估和改进的相同(ϵ 贪婪策略)策略选择动作。
- Sarsamax 是离线策略方法,我们会评估和改进(ϵ 贪婪)策略,并根据另一个策略选择动作。
- 既定策略 TD 控制方法(例如预期 Sarsa 和 Sarsa)的在线效果比新策略 TD 控制方法(例如 Sarsamax)的要好。
- 预期 Sarsa 通常效果比 Sarsa 的要好。
如果你要了解详情,建议阅读该教科书(尤其是第 6.4-6.6 部分)的第 6 章节。
迷你项目:时间差分方法
在 CliffWalking 环境中,智能体会浏览一个 4x12 网格世界。请在该教科书的示例 6.6 中详细了解悬崖行走任务。阅读完毕后,你可以打开相应的 GitHub 文件并阅读 CliffWalkingEnv 类中的注释部分,详细了解该环境。
第 0 部分:探索 CliffWalkingEnv
请使用以下代码单元格创建 CliffWalking 环境的实例。
import gym
env = gym.make('CliffWalking-v0')
智能体会在 4×124×12 网格世界中移动,状态编号如下所示:
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]]
在任何阶段开始时,初始状态都是状态 36。状态 47是唯一的终止状态,悬崖对应的是状态 37 到 46。
智能体可以执行 4 个潜在动作:
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
因此,S+={0,1,…,47} 以及 A={0,1,2,3}。请通过运行以下代码单元格验证这一点。
print(env.action_space)
print(env.observation_space)
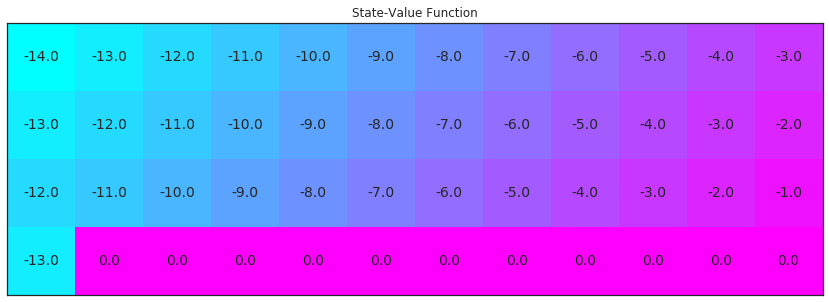
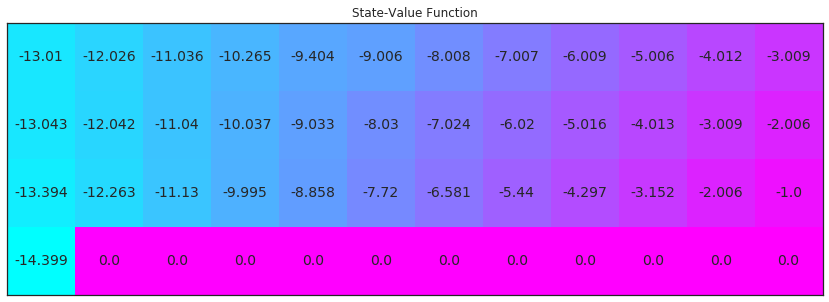
在此迷你项目中,我们将逐步发现 CliffWalking 环境的最优策略。最优状态值函数可视化结果如下。请立即花时间确保理解为何 这是最优状态值函数。
import numpy as np
from plot_utils import plot_values
# define the optimal state-value function
V_opt = np.zeros((4,12))
V_opt[0:13][0] = -np.arange(3, 15)[::-1]
V_opt[0:13][1] = -np.arange(3, 15)[::-1] + 1
V_opt[0:13][2] = -np.arange(3, 15)[::-1] + 2
V_opt[3][0] = -13
plot_values(V_opt)
第 1 部分:TD 预测 - 状态值
在此部分,你将自己编写 TD 预测的实现(用于估算状态值函数)。
我们首先将研究智能体按以下方式移动的策略:
- 在状态
0到10(含)时向RIGHT移动, - 在状态
11、23和35时向DOWN移动, - 在状态
12到22(含)、状态24到34(含)和状态36时向UP移动。
下面指定并输出了该策略。注意,智能体没有选择动作的状态被标记为 -1。
policy = np.hstack([1*np.ones(11), 2, 0, np.zeros(10), 2, 0, np.zeros(10), 2, 0, -1*np.ones(11)])
print("\nPolicy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy.reshape(4,12))
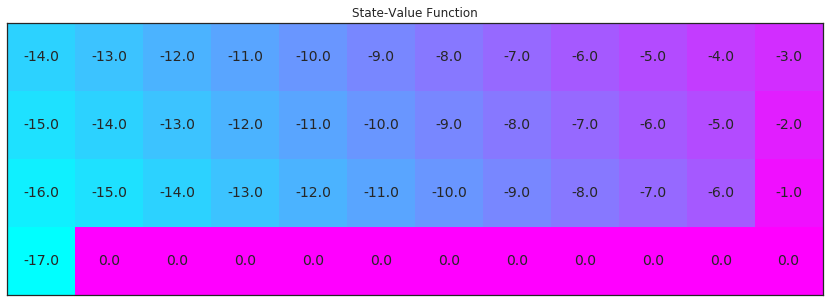
请运行下个单元格,可视化与此策略相对应的状态值函数。你需要确保花时间来理解为何这是对应的值函数!
V_true = np.zeros((4,12))
for i in range(3):
V_true[0:12][i] = -np.arange(3, 15)[::-1] - i
V_true[1][11] = -2
V_true[2][11] = -1
V_true[3][0] = -17
plot_values(V_true)
你将通过 TD 预测算法尝试逼近上图的结果。
你的 TD 预测算法将包括 5 个参数:
env:这是 OpenAI Gym 环境的实例。num_episodes:这是通过智能体-环境互动生成的阶段次数。policy:这是一个一维 numpy 数组,其中policy.shape等于状态数量 (env.nS)。policy[s]返回智能体在状态s时选择的动作。alpha:这是更新步骤的步长参数。gamma:这是折扣率。它必须是在 0 到 1(含)之间的值,默认值为:1。
该算法会返回以下输出结果:
V:这是一个字典,其中V[s]是状态s的估算值。
请完成以下代码单元格中的函数。
from collections import defaultdict, deque
import sys
def td_prediction(env, num_episodes, policy, alpha, gamma=1.0):
# initialize empty dictionaries of floats
V = defaultdict(float)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# begin an episode, observe S
state = env.reset()
while True:
# choose action A
action = policy[state]
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# perform updates
V[state] = V[state] + (alpha * (reward + (gamma * V[next_state]) - V[state]))
# S <- S'
state = next_state
# end episode if reached terminal state
if done:
break
return V
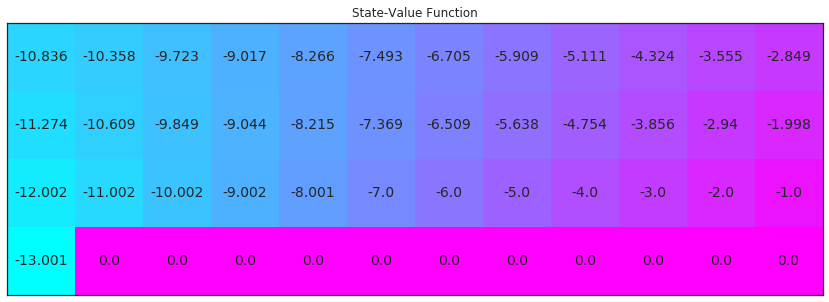
请运行以下代码单元格,以测试你的实现并可视化估算的状态值函数。如果代码单元格返回 PASSED,则表明你正确地实现了该函数!你可以随意更改提供给该函数的 num_episodes 和 alpha 参数。但是,如果你要确保单元测试的准确性,请勿更改 gamma 的默认值。
import check_test
# evaluate the policy and reshape the state-value function
V_pred = td_prediction(env, 5000, policy, .01)
# please do not change the code below this line
V_pred_plot = np.reshape([V_pred[key] if key in V_pred else 0 for key in np.arange(48)], (4,12))
check_test.run_check('td_prediction_check', V_pred_plot)
plot_values(V_pred_plot)
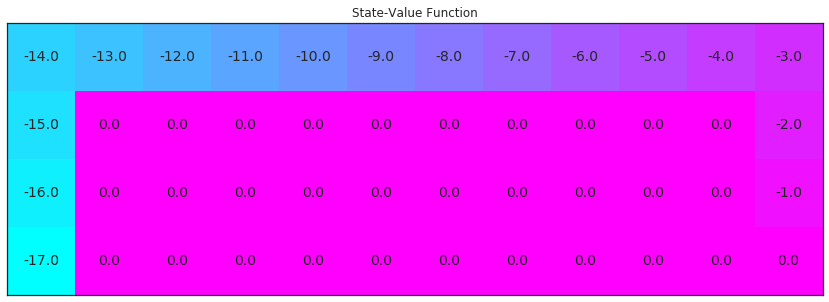
你的估算状态值函数与该策略对应的真状态值函数有多接近?
你可能注意到了,有些状态值不是智能体估算的。因为根据该策略,智能体不会经历所有状态。在 TD 预测算法中,智能体只能估算所经历的状态对应的值。
第 2 部分:TD 控制 - Sarsa
在此部分,你将自己编写 Sarsa 控制算法的实现。
你的算法将有四个参数:
env:这是 OpenAI Gym 环境的实例。num_episodes:这是通过智能体-环境互动生成的阶段次数。alpha:这是更新步骤的步长参数。gamma:这是折扣率。它必须是在 0 到 1(含)之间的值,默认值为:1。
该算法会返回以下输出结果:
Q:这是一个字典(一维数组),其中Q[s][a]是状态s和动作a对应的估算动作值。
请完成以下代码单元格中的函数。
(你可以随意定义其他函数,以帮助你整理代码。)
def update_Q(Qsa, Qsa_next, reward, alpha, gamma):
""" updates the action-value function estimate using the most recent time step """
return Qsa + (alpha * (reward + (gamma * Qsa_next) - Qsa))
def epsilon_greedy_probs(env, Q_s, i_episode, eps=None):
""" obtains the action probabilities corresponding to epsilon-greedy policy """
epsilon = 1.0 / i_episode
if eps is not None:
epsilon = eps
policy_s = np.ones(env.nA) * epsilon / env.nA
policy_s[np.argmax(Q_s)] = 1 - epsilon + (epsilon / env.nA)
return policy_s
import matplotlib.pyplot as plt
%matplotlib inline
def sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode, observe S
state = env.reset()
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode)
# pick action A
action = np.random.choice(np.arange(env.nA), p=policy_s)
# limit number of time steps per episode
for t_step in np.arange(300):
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
if not done:
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[next_state], i_episode)
# pick next action A'
next_action = np.random.choice(np.arange(env.nA), p=policy_s)
# update TD estimate of Q
Q[state][action] = update_Q(Q[state][action], Q[next_state][next_action],
reward, alpha, gamma)
# S <- S'
state = next_state
# A <- A'
action = next_action
if done:
# update TD estimate of Q
Q[state][action] = update_Q(Q[state][action], 0, reward, alpha, gamma)
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
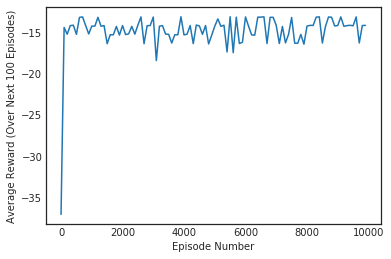
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
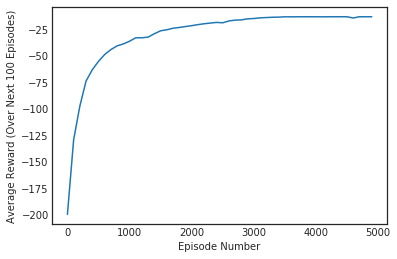
请使用下个代码单元格可视化估算的最优策略和相应的状态值函数。
如果代码单元格返回 PASSED,则表明你正确地实现了该函数!你可以随意更改提供给该函数的 num_episodes 和 alpha 参数。但是,如果你要确保单元测试的准确性,请勿更改 gamma 的默认值。
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsa = sarsa(env, 5000, .01)
# print the estimated optimal policy
policy_sarsa = np.array([np.argmax(Q_sarsa[key]) if key in Q_sarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_sarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsa)
# plot the estimated optimal state-value function
V_sarsa = ([np.max(Q_sarsa[key]) if key in Q_sarsa else 0 for key in np.arange(48)])
plot_values(V_sarsa)
第 3 部分:TD 控制 - Q 学习
在此部分,你将自己编写 Q 学习控制算法的实现。
你的算法将有四个参数:
env:这是 OpenAI Gym 环境的实例。num_episodes:这是通过智能体-环境互动生成的阶段次数。alpha:这是更新步骤的步长参数。gamma:这是折扣率。它必须是在 0 到 1(含)之间的值,默认值为:1。
该算法会返回以下输出结果:
Q:这是一个字典(一维数组),其中Q[s][a]是状态s和动作a对应的估算动作值。
请完成以下代码单元格中的函数。
(你可以随意定义其他函数,以帮助你整理代码。)
def q_learning(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode, observe S
state = env.reset()
while True:
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode)
# pick next action A
action = np.random.choice(np.arange(env.nA), p=policy_s)
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
# update Q
Q[state][action] = update_Q(Q[state][action], np.max(Q[next_state]), \
reward, alpha, gamma)
# S <- S'
state = next_state
# until S is terminal
if done:
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
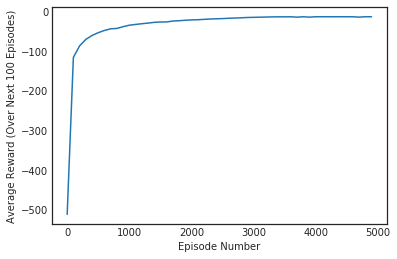
请使用下个代码单元格可视化估算的最优策略和相应的状态值函数。
如果代码单元格返回 PASSED,则表明你正确地实现了该函数!你可以随意更改提供给该函数的 num_episodes 和 alpha 参数。但是,如果你要确保单元测试的准确性,请勿更改 gamma 的默认值。
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsamax = q_learning(env, 5000, .01)
# print the estimated optimal policy
policy_sarsamax = np.array([np.argmax(Q_sarsamax[key]) if key in Q_sarsamax else -1 for key in np.arange(48)]).reshape((4,12))
check_test.run_check('td_control_check', policy_sarsamax)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsamax)
# plot the estimated optimal state-value function
plot_values([np.max(Q_sarsamax[key]) if key in Q_sarsamax else 0 for key in np.arange(48)])
第 4 部分:TD 控制 - 预期 Sarsa
在此部分,你将自己编写预期 Sarsa 控制算法的实现。
你的算法将有四个参数:
env:这是 OpenAI Gym 环境的实例。num_episodes:这是通过智能体-环境互动生成的阶段次数。alpha:这是更新步骤的步长参数。gamma:这是折扣率。它必须是在 0 到 1(含)之间的值,默认值为:1。
该算法会返回以下输出结果:
Q:这是一个字典(一维数组),其中Q[s][a]是状态s和动作a对应的估算动作值。
请完成以下代码单元格中的函数。
(你可以随意定义其他函数,以帮助你整理代码。)
def expected_sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode
state = env.reset()
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode, 0.005)
while True:
# pick next action
action = np.random.choice(np.arange(env.nA), p=policy_s)
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
# get epsilon-greedy action probabilities (for S')
policy_s = epsilon_greedy_probs(env, Q[next_state], i_episode, 0.005)
# update Q
Q[state][action] = update_Q(Q[state][action], np.dot(Q[next_state], policy_s), \
reward, alpha, gamma)
# S <- S'
state = next_state
# until S is terminal
if done:
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
请使用下个代码单元格可视化估算的最优策略和相应的状态值函数。
如果代码单元格返回 PASSED,则表明你正确地实现了该函数!你可以随意更改提供给该函数的 num_episodes 和 alpha 参数。但是,如果你要确保单元测试的准确性,请勿更改 gamma 的默认值。
# obtain the estimated optimal policy and corresponding action-value function
Q_expsarsa = expected_sarsa(env, 10000, 1)
# print the estimated optimal policy
policy_expsarsa = np.array([np.argmax(Q_expsarsa[key]) if key in Q_expsarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_expsarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_expsarsa)
# plot the estimated optimal state-value function
plot_values([np.max(Q_expsarsa[key]) if key in Q_expsarsa else 0 for key in np.arange(48)])
posted on 2019-02-21 20:54 paulonetwo 阅读(643) 评论(0) 编辑 收藏 举报