机器学习工程师 - Udacity 强化学习 Part Two

三、强化学习框架：解决方案
1.状态值函数

2.贝尔曼方程

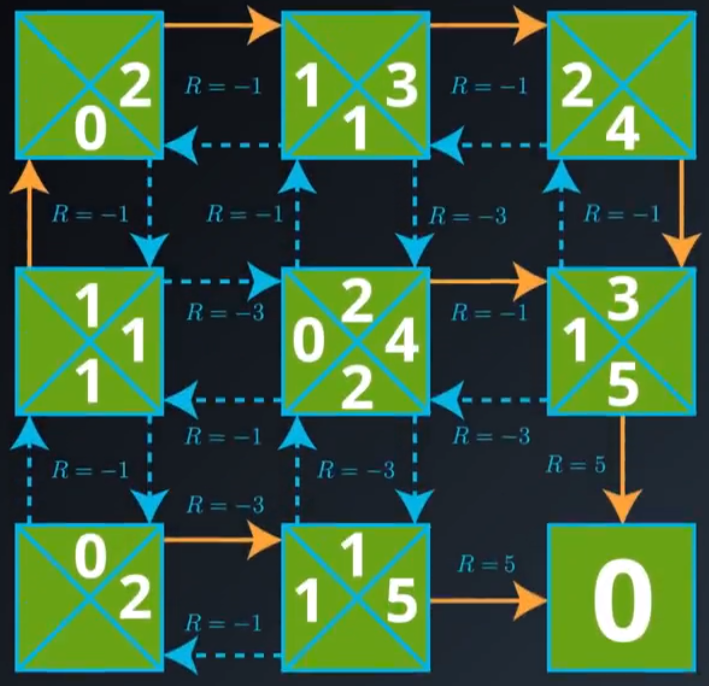
在这个网格世界示例中，一旦智能体选择一个动作，
1)它始终沿着所选方向移动（而一般 MDP 则不同，智能体并非始终能够完全控制下个状态将是什么）
2)可以确切地预测奖励（而一般 MDP 则不同，奖励是从概率分布中随机抽取的）。
在这个简单示例中，我们发现任何状态的值可以计算为即时奖励和下个状态（折扣）值的和。
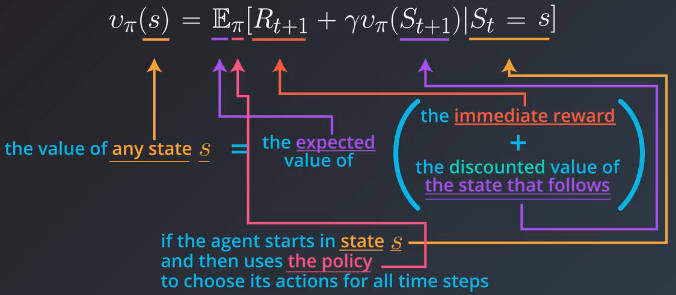
对于一般 MDP，我们需要使用期望值，因为通常即时奖励和下个状态无法准确地预测，奖励和下个状态是根据 MDP 的一步动态特性选择的。在这种情况下，奖励 r 和下个状态 s' 是从（条件性）概率分布 p(s',r|s,a) 中抽取的，贝尔曼预期方程（对于 v_π）表示了任何状态 s 对于预期即时奖励和下个状态的预期值的值：
v_π(s)=E_π[R_t+1+γv_π(S_t+1)∣S_t=s].
计算预期值
如果智能体的策略 π 是确定性策略，智能体在状态 s 选择动作 π(s)，贝尔曼预期方程可以重写为两个变量 (s 和 r) 的和：
v_π(s)=∑_{s′∈S⁺,r∈R}p(s′,r∣s,π(s))(r+γv_π(s′))
在这种情况下，我们将奖励和下个状态的折扣值之和 (r+γv_π(s′)) 与相应的概率 p(s′,r∣s,π(s)) 相乘，并将所有概率相加得出预期值。
如果智能体的策略 π 是随机性策略，智能体在状态 s 选择动作 a 的概率是 π(a∣s)，贝尔曼预期方程可以重写为三个变量（s' 、r 和 a）的和：
v_π(s)=∑_{s′∈S⁺,r∈R,a∈A(s)}π(a∣s)p(s′,r∣s,a)(r+γv_π(s′))
在这种情况下，我们将奖励和下个状态的折扣值之和 (r+γv_π(s′)) 与相应的概率 π(a∣s)p(s′,r∣s,a) 相乘，并将所有概率相加得出预期值。

3.动作值函数
 

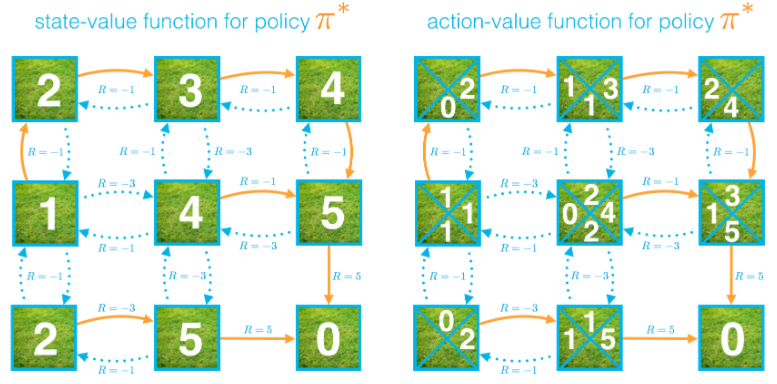
4.最优性

5.对于确定性策略 π，v_π​(s)=q_π​(s,π(s))适用于所有 s∈S：

6.最优策略
智能体与环境互动，通过该互动，估算出最优动作值函数，然后智能体使用该值函数得出最优策略。
如果状态空间 S 和动作空间 A 是有限的，我们可以用表格表示最优动作值函数 q_∗，每个可能的环境状态 s∈S 和动作 a∈A 对应一个策略。
特定状态动作对 s,a 的值是智能体从状态 s 开始并采取动作 a，然后遵守最优策略 π_∗所获得的预期回报。
我们在下方为虚拟马尔可夫决策流程 (MDP) (where S={s₁,s₂,s₃} 和 A={a₁,a₂,a₃}) 填充了一些值。

智能体确定最优动作值函数 q_∗后，它可以为所有 s∈S 设置 π_∗(s)=argmax_a∈A(s)q_∗(s,a) 快速获得最优策略 π_∗。
要了解为何是这种情况，注意，必须确保 v_∗(s)=max_a∈A(s)q_∗(s,a)。
如果在某个状态 s∈S 中，a∈A(s) 可以最大化最优动作值函数，你可以通过向任何（最大化）状态分配任意大小的概率构建一个最优策略。只需确保根据该策略给不会最大化动作值函数的动作（对于特定状态）分配的概率是 0% 即可。
为了构建最优策略，我们可以先在每行（或每个状态）中选择最大化动作值函数的项。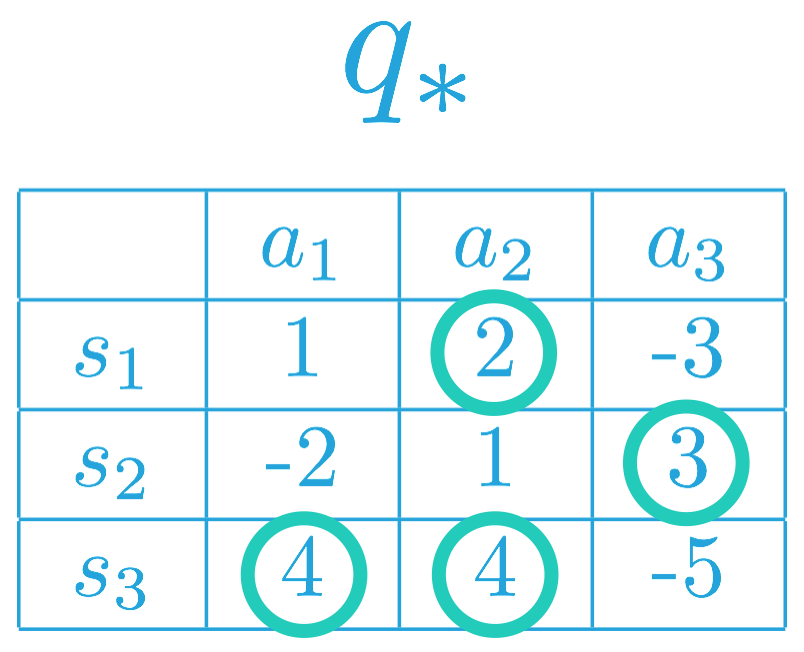

因此，相应 MDP 的最优策略 π_∗ 必须满足：
π_∗(s₁) = a₂(or, equivalently, π_∗(a₂∣s₁)=1)，以及
π_∗(s₂)=a₃(or, equivalently, π_∗(a₃∣s₂)=1)。
这是因为 a₂=argmax_a∈A(s1)q_∗(s,a)，以及 a₃=argmax_a∈A(s2)q_∗(s,a)。
换句话说，在最优策略下，智能体在状态 s₁下必须选择动作 a₂，在状态 s₂下将选择动作 a₃。
对于状态 s₃，注意 a₁,a₂∈argmax_a∈A(s3)q_∗(s,a)。因此，智能体可以根据最优策略选择动作 a₁或 a₂，但是始终不能选择动作 a₃。即最优策略 π_∗ 必须满足：
π_∗(a₁∣s₃)=p，
π_∗(a₂∣s₃)=q，以及
π_∗(a₃∣s₃)=0，
其中 p,q≥0 以及 p+q=1。

7.贝尔曼方程（第 2 部分）
有两组贝尔曼方程：(1) 贝尔曼预期方程 和 (2) 贝尔曼最优性方程。每组方程包含两个方程，对应于状态值或动作值。
所有贝尔曼方程对有限马尔可夫决策流程 (MDP) 来说都非常有用。

贝尔曼预期方程
我们已经介绍了 v_π 的贝尔曼预期方程
v_π(s)=E_π[R_t+1+γv_π(S_t+1)∣S_t=s]。
对于任意随机性策略 π，该方程可以表示为
v_π(s)=∑_{s′∈S⁺,r∈R,a∈A(s)}π(a∣s)p(s′,r∣s,a)(r+γv_π(s′))。
该方程表示了任何状态（根据任意策略）相对于后续状态（根据同一策略）的值。
q_π的贝尔曼预期方程是：
q_π(s,a)=E_π[R_t+1+γq_π(S_t+1,A_t+1)∣S_t=s,A_t=a]=∑_{s′∈S⁺,r∈R}p(s′,r∣s,a)(r+γ∑_a′∈A(s)π(a′∣s′)q_π(s′,a′))
其中最后一个形式详细介绍了如何计算任意随机策略 π 的预期值。该方程表示任何状态动作对（根据任意策略）相对于后续状态的值（根据同一策略）的值。

贝尔曼最优性方程
和贝尔曼预期方程相似，贝尔曼最优性方程可以证明：状态值（以及动作值函数）满足递归关系，可以将状态值（或状态动作对的值）与所有后续状态（或状态动作对）的值联系起来。
虽然贝尔曼最优性方程关心的是任意策略，但是贝尔曼最优性方程完全侧重于最优策略对应的值满足的关系。
v_∗的贝尔曼最优性方程是：
v_∗(s)=max_a∈A(s)E[R_t+1+γv_∗(S_t+1)∣S_t=s]=max_a∈A(s)∑_{s′∈S⁺,r∈R}p(s′,r∣s,a)(r+γv_∗(s′))
它表示任何状态根据最优策略相对于后续状态的值（根据最优策略）的值。
q_∗的贝尔曼最优性方程是：
q_∗(s,a)=E[R_t+1+γmax_{a′∈A(St+1)}q_∗(S_t+1,a′)∣S_t=s,A_t=a]=∑_{s′∈S⁺,r∈R}p(s′,r∣s,a)(r+γmax_{a′∈A(s′)}q_∗(s′,a′))
它表示任何状态动作对根据最优策略相对于后续状态动作对（根据最优策略）的值的值。

实用公式
为了推导出所有四个贝尔曼方程，有必要先推导出紧密相关的公式。
q_π(s,a)=∑_{s′∈S⁺,r∈R}p(s′,r∣s,a)(r+γv_π(s′)) (方程 1)
该方程表示相对于状态值函数和 MDP 一步动态特性的策略动作值函数。
我们将提供两个论证来证明该方程，一个是对话论证，另一个是代数论证。
求导 1
我们将先从会话参数开始。当智能体位于状态 s 并采取动作 a 时，可以产生任何数量的潜在下个状态 s′ 和奖励 r。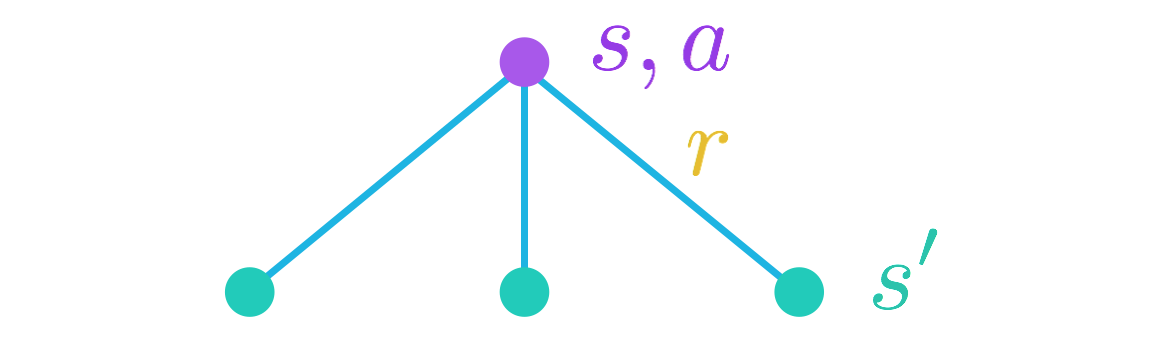

如果下个状态 s′ 和奖励 r 可以确切地预测，那么回报可以计算为 r+γv_π​(s′)。
知道这一点后，为了获得动作值 q_π​(s,a)，我们只需计算和 r+γv_π​(s′) 的预期值。可以通过以下方程获得
q_π​(s,a)=∑_{s′∈S⁺,r∈R}​p(s′,r∣s,a)(r+γv_π​(s′))，
其中每个 s',r 对的概率由 MDP 的一步动态特性 p(s′,r∣s,a) 确定。
求导 2
请算出以下方程 1 的替代导数。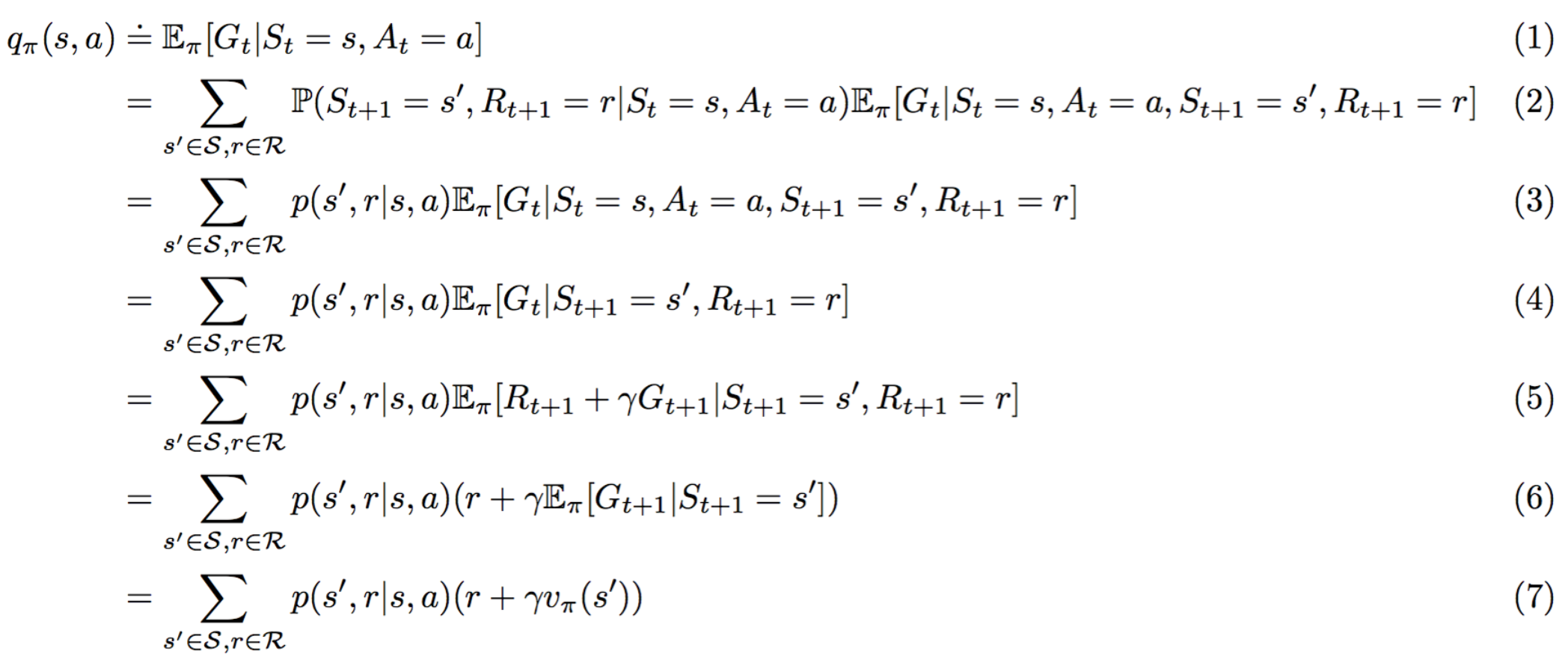

理由如下：
(1) 满足 q_π​(s,a)=E_π​[G_t​∣S_t​=s,A_t​=a] 的定义。
(2) 遵守全期望公式。
(3) 根据定义 p(s′,r∣s,a)=P(S_t+1​=s′,R_t+1​=r∣S_t​=s,A_t​=a) 是正确的
(4) 满足，因为 E_π​[G_t​∣S_t​=s,A_t​=a,S_t+1​=s′,R_t+1​=r]=E_π​[G_t​∣S_t+1​=s′,R_t+1​=r]。
(5) 遵守，因为 G_t​=R_t+1​+γG_t+1​。
(6) 根据线性期望是正确的。
(7) 根据定义 v_π​(s′):=E_π​[G_t​∣S_t​=s′]=E_π​[G_t+1​∣S_t+1​=s′] 是正确的。

得出贝尔曼预期方程
为了得出贝尔曼预期方程，我们需要使用另一个公式。
v_π​(s)=∑_a∈A(s)​π(a∣s)q_π​(s,a)（方程 2）
该方程使我们能够根据（潜在随机性）策略对应的动作值函数获得状态值函数。
v_π​ 的贝尔曼预期方程可以通过先从方程 2 开始并用方程 1 替换 q_π​(s,a) 的值获得。
同样，q_π​ 的贝尔曼预期方程可以通过先从方程 1 开始并用方程 2 替换 v_π​(s) 的值获得。

获得贝尔曼最优性方程
为了推出贝尔曼最优性方程，我们需要另外两个方程。
q_∗​(s,a)=∑_{s′∈S⁺,r∈R}​p(s′,r∣s,a)(r+γv_∗​(s′)) (方程 3)
方程 3 表示相对于最优状态值函数和 MDP 一步动态特性的最优动作值函数。
v_∗​(s)=max_a∈A(s)​q_∗​(s,a) (方程 4)
方程 4 表示相对于最优动作值函数的最优状态值函数。
v_∗​ 的贝尔曼最优性方程可以通过先从方程 4 开始并用方程 3 替换 q_∗​(s,a) 的值获得。
q_∗​ 的贝尔曼最优性方程可以通过先从方程 3 开始并用方程 4 替换 v_∗​(s) 的值获得。