lc0324
✅ 119. 杨辉三角 II
https://leetcode-cn.com/problems/pascals-triangle-ii/
描述
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
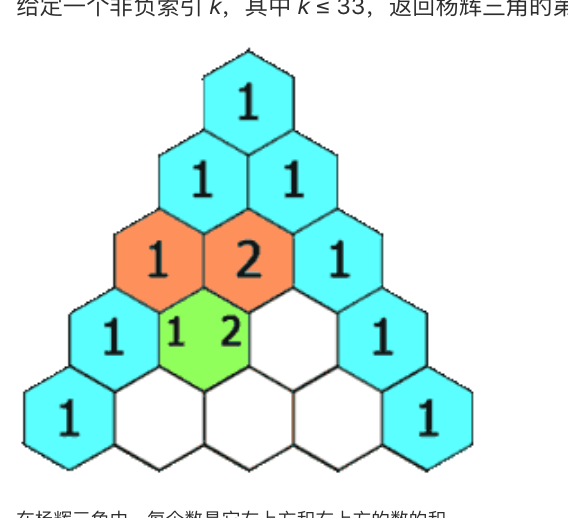
解答
他人:
c/Java
/**
* 获取杨辉三角的指定行
* 直接使用组合公式C(n,i) = n!/(i!*(n-i)!)
* 则第(i+1)项是第i项的倍数=(n-i)/(i+1);
*/
public List<Integer> getRow(int rowIndex) {
List<Integer> res = new ArrayList<>(rowIndex + 1);
long cur = 1;
for (int i = 0; i <= rowIndex; i++) {
res.add((int) cur);
cur = cur * (rowIndex-i)/(i+1);
}
return res;
}
---
int* getRow(int rowIndex, int* returnSize) {
*returnSize = rowIndex + 1;
int* num = (int*) malloc ((rowIndex + 1) * sizeof(int));
for(int i = 0;i <= rowIndex;i++)
for(int j = i;j >= 0;j--)
{
if(j == 0 || j == i)
num[j] = 1;
else
num[j] = num[j] + num[j-1];
}
return num;
}
---
java beats 98%
public List<Integer> getRow(int rowIndex) {
Integer[] dp = new Integer[rowIndex + 1];
Arrays.fill(dp,1);
for(int i = 2;i < dp.length;i++){
for(int j = i - 1;j > 0;j--)
dp[j] = dp[j] + dp[j - 1];
}
List<Integer> res = Arrays.asList(dp);
return res;
}` 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
py
class Solution:
def getRow(self, rowIndex: int) -> List[int]:
res = []
for i in range(1, rowIndex):
tmp = [1] * i
for j in range(1, i-1):
tmp[j] = res[i-1][j-1] + res[i-1][j]
res.append(tmp)
return res[rowIndex-1]
'''
最后一行:红了:
IndexError: list index out of range
Line 9 in getRow (Solution.py)
Line 34 in _driver (Solution.py)
Line 45 in <module> (Solution.py)
'''
######fix:
class Solution:
def getRow(self, rowIndex: int) -> List[int]:
res = []
for i in range(1, rowIndex+2):
tmp = [1] * i
for j in range(1, i-1):
tmp[j] = res[i-2][j-1] + res[i-2][j]
res.append(tmp)
print(res)
return res[rowIndex]
'''
执行用时 :
44 ms
, 在所有 Python3 提交中击败了
28.65%
的用户
内存消耗 :
13.6 MB
, 在所有 Python3 提交中击败了
5.16%
的用户
'''




