子集生成

子集生成

给定一个集合，枚举所有可能的子集。在这里的集合是{0,1,2...n-1}

1.增量构造法

感觉紫书上这段代码不是很好理解，画了一个图来辅助理解。这里的集合是{0,1,2...n-1}，也可以看作是下标的集合，对任意集合，只要能输出它的下标的子集，也就能够输出该集合的子集。
这段代码还使用了定序的技巧，即所有元素是从小到大排列，在输出{1,2}后就不会输出{2,1}了，细细体会。
增量法的解答树共有\(2^n\)个结点，因为每个可能的A都对应一个结点，n元集合就有\(2^n\)个子集。

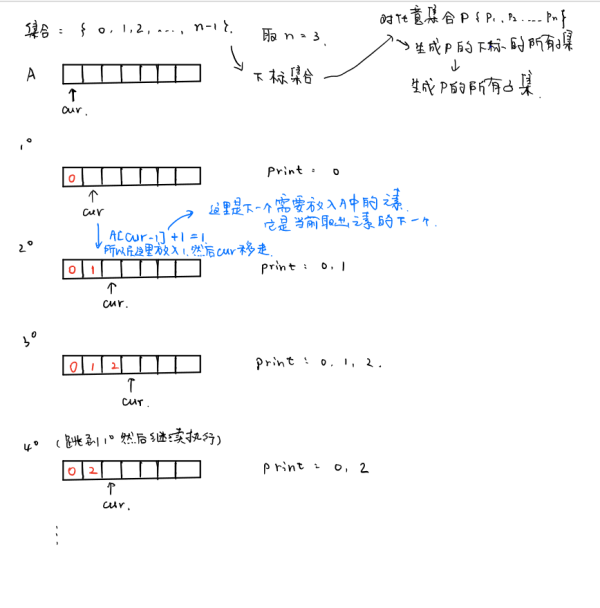
代码：

void print_subset(int n, int* A, int cur){
	for(int i = 0; i < cur; ++i) printf("%d", A[i]); //打印当前集合
	printf("\n");
	int s = cur ? A[cur-1] :  0;          //确定当前元素的最小可能值
	for(int i = s; i < n; ++i){
		A[cur] = s;
		print_subset(n, A, cur+1);         //递归构造子集
	}
}

2.位向量法

构造一个位向量B[i]，当B[i]=1，i在子集A中。通过位向量法的解答树能够理解，这里的解答树结点的结点总数为2047个，比增量构造法多，因为包含了部分解。

解答树的结点，我的理解是每次递归调用自身，就产生一个结点。

代码：

void print_subset(int n, int *B, int cur){
	if(cur == n){
		for(int i = 0; i < n; ++i)
			if(B[i]) printf("%d ", i);
		printf("\n");
		return;
	}
	B[cur] = 1;
	print_subset(n, B, cur+1);
	B[cur] = 0;
	print_subset(n, B, cur+1);
}

3.位运算法

代码：

void print_subset(int n, int i){
	for(int s = 0; s < n; ++s){
		if(i & (1<<s)) printf("%d ", s);
	printf("\n");
	}
}

for(int i = 0; i < (1<<n); ++i)
	print_subset(n, i);