20230415 训练记录:全路径计数 / dp
傻逼博客园,写好的文章不是自动保存在草稿箱,而是这个打开的网页。然后傻逼 Windows 自动更新使得断电退出这个网页,写的几百行文章没了。操了。
全路径计数
关于全路径计数,大前天 已经给出两例,今日再加一例。一般来说,点权和边权的做法是不一样的,所以分开来说。
全路径颜色统计(点权)
考虑对于每种颜色,统计其没有出现在某些子树中,用总的把这些减去就是答案。特殊的,将根节点看作有全部颜色。
展开代码
#include <bits/stdc++.h>
using ll = long long;
const int N = 200010;
int n, _cnt, h[N];
struct edge {
int f, t;
} edges[N * 2];
void link(int u, int v) {
edges[++_cnt] = { v, h[u] }, h[u] = _cnt;
}
int s[N], c[N], v[N], cnt[N];
ll sub = 0;
void dfs(int u, int p) {
s[u] = 1;
int sum = 0;
for (int i = h[u]; i; i = edges[i].t) {
int v = edges[i].f;
if (v != p) {
int t = cnt[c[u]];
dfs(v, u);
s[u] += s[v];
int partial = s[v] - (cnt[c[u]] - t);
sub += 1LL * partial * (partial - 1) / 2;
sum += partial;
}
}
cnt[c[u]] += sum + 1;
}
int main() {
int _case = 0;
while (~scanf("%d", &n)) {
_cnt = sub = 0;
std::fill_n(h, n + 1, 0);
std::fill_n(v, n + 1, 0);
std::fill_n(c, n + 1, 0);
std::fill_n(cnt, n + 1, 0);
int tot = 0;
for (int i = 1; i <= n; i++) {
scanf("%d", c + i);
if (!v[c[i]]) {
tot += v[c[i]] = 1;
}
}
ll ans = 1LL * tot * n * (n - 1) / 2;
for (int i = 1, u, v; i < n; i++) {
scanf("%d%d", &u, &v);
link(u, v), link(v, u);
}
dfs(1, 0);
for (int i = 1; i <= n; i++) {
if (v[i]) {
sub += 1LL * (n - cnt[i]) * (n - cnt[i] - 1) / 2;
}
}
printf("Case #%d: %lld\n", ++_case, ans - sub);
}
return 0;
}
全路径颜色统计(边权)
考虑每一条边,对于其颜色 \(w\),向上有 \(c_w\) 个点使得不经过颜色 \(w\)。那么贡献为 \(\mathcal{size}_v (c_w - \mathcal{size}_v)\),递归下去的时候限制向上最多走 \(\mathcal{size}_v\)。
问题的关键,在于回溯的时候如何避免多算了,可以在 dive 下去的时候,记下 \(t := c_w\),回溯之后成为 \(c_w := t - \mathcal{size}_v\)。
展开代码
void cal(int u, int p) {
for (int i = h[u]; i; i = edges[i].t) {
if (int v = edges[i].f, w = edges[i].w; v != p) {
ans += 1LL * s[v] * (c[w] - s[v]);
int t = c[w];
c[w] = s[v];
cal(v, u);
c[w] = t - s[v];
}
}
}
2017 沈阳 L. Tree
\(n\) 个节点的一棵树,\(k\) 种颜色,将每个节点安排上一种颜色。对于颜色 \(i\),将所有涂上 \(i\) 颜色的节点用最短路连接起来,得到边集 \(E_i\)。那么 \(\bigcap\limits_{i = 1}^kE_i\) 最大多大?
对于某一条边,只要左右两边都有至少 \(k\) 个节点,就能够被选中。因此问题转变为对于每一棵子树内外节点数是否都 \(\geq k\),一次 DFS 便可解决。
三元环计数 Counting Stars
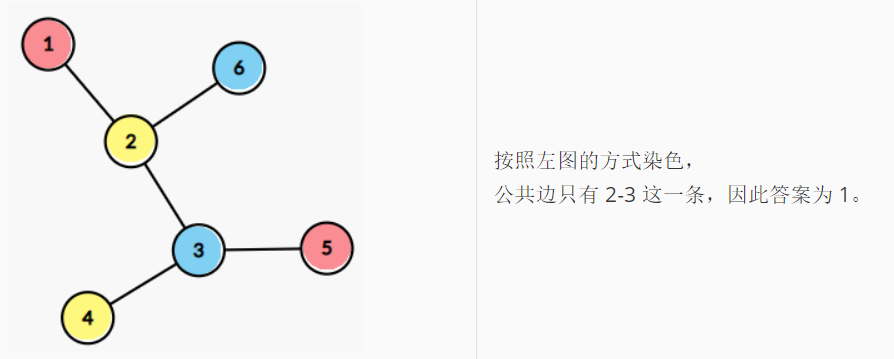
求有一条公共边的双三元环数量。
套用 \(\mathcal O(m \sqrt m)\) 的模板。
- 小于 \(\sqrt m\) 的:\(\{u\}\) 子节点 \(\{v\}\) 中前驱是 \(i\) 的那些点即为所求。
- 大于 \(\sqrt m\) 的:从 \(i\) 出发的 \(\{v\}\) 中曾经连接了一条 \(u \rightarrow v\)。
展开代码
#include <bits/stdc++.h>
using ll = long long;
const ll maxn = 100000;
ll con(int x, int y) {
return x * maxn + y;
}
int main() {
int n, m;
std::cin.tie(nullptr)->sync_with_stdio(false);
while (std::cin >> n >> m) {
std::vector<std::vector<int>> g(n);
std::vector<int> dep(n), pre(n, -1), vis(n);
std::unordered_set<long long> S;
for (int i = 0; i < m; i++) {
int u, v;
std::cin >> u >> v;
u -= 1, v -= 1;
g[u].push_back(v);
g[v].push_back(u);
dep[u] += 1, dep[v] += 1;
S.insert(con(u, v));
S.insert(con(v, u));
}
ll ans{};
const int t = std::sqrt(m + .5);
for (int i = 0; i < n; i++) {
vis[i] = 1;
for (int u : g[i]) {
pre[u] = i;
}
for (int u : g[i]) if (!vis[u]) {
int cnt{};
if (dep[u] <= t) {
for (int v : g[u]) {
cnt += pre[v] == i;
}
} else {
for (int v : g[i]) {
cnt += S.count(con(u, v));
}
}
ans += 1LL * cnt * (cnt - 1) / 2;
}
}
std::cout << ans << "\n";
}
return 0;
}
2023 Acwing 春季每日一题
二叉树遍历
冶炼金属
飞机降落
std::next_permutation 再计算会造成许多重复计算。
展开代码
void solve() {
int n; std::cin >> n;
std::vector<std::tuple<int, int, int>> g(n);
for (auto &[t, d, l] : g) std::cin >> t >> d >> l;
std::vector<int> v(n);
std::cout << ([&, dfs{[&](auto &&self, int u, int time) -> bool {
if (u > n) return true;
for (int i = 0; i < n; i++) if (!v[i]) {
auto &[t, d, l] = g[i];
int s = std::max(time, t);
if (s > t + d) return false;
s += l;
v[i] = 1;
if (self(self, u + 1, s)) return true;
v[i] = 0;
}
return {};
}}] {
return dfs(dfs, 1, 0);
}() ? "YES" : "NO") << '\n';
}
接龙数列
子矩阵
单调队列模板,tedious。
展开代码
#include <bits/stdc++.h>
using ll = long long;
const int mod = 998244353;
int main() {
std::cin.tie(nullptr)->sync_with_stdio(false);
int n, m, a, b; std::cin >> n >> m >> a >> b;
std::vector g(n, std::vector(m, 0)); for (auto &i : g) for (auto &j : i) std::cin >> j;
auto g1 = g, g2 = g, g3 = g;
for (int i = 0; i < n; i++) {
std::deque<int> dq;
for (int j = 0; j < m ;j++) {
while (!dq.empty() && dq.back() <= j - b) dq.pop_back();
while (!dq.empty() && g[i][dq.front()] > g[i][j]) dq.pop_front();
dq.push_front(j);
g1[i][j] = g[i][dq.back()];
}
}
for (int j = 0; j < m ;j++) {
std::deque<int> dq;
for (int i = 0; i < n; i++) {
while (!dq.empty() && dq.back() <= i - a) dq.pop_back();
while (!dq.empty() && g1[dq.front()][j] > g1[i][j]) dq.pop_front();
dq.push_front(i);
g2[i][j] = g1[dq.back()][j];
}
}
for (int i = 0; i < n; i++) {
std::deque<int> dq;
for (int j = 0; j < m ;j++) {
while (!dq.empty() && dq.back() <= j - b) dq.pop_back();
while (!dq.empty() && g[i][dq.front()] < g[i][j]) dq.pop_front();
dq.push_front(j);
g1[i][j] = g[i][dq.back()];
}
}
for (int j = 0; j < m ;j++) {
std::deque<int> dq;
for (int i = 0; i < n; i++) {
while (!dq.empty() && dq.back() <= i - a) dq.pop_back();
while (!dq.empty() && g1[dq.front()][j] < g1[i][j]) dq.pop_front();
dq.push_front(i);
g3[i][j] = g1[dq.back()][j];
}
}
ll ans = 0;
a -= 1, b -= 1;
for (int i = a; i < n; i++) {
for (int j = b; j < m; j++) {
ans = (ans + 1LL * g2[i][j] * g3[i][j]) % mod;
}
}
std::cout << ans << '\n';
return 0;
}
skew数
Atcoder dp Education Contest
Frog 1
呱呱可以从 \(i\) 跳到 \(i + 1\) 和 \(i + 2\),花费分别 \(|a_i - a_{i + 1}|\) 和 \(|a_i - a_{i + 2}|\)。求从 \(1\) 到 \(n\) 的最小花费和。
直接转移,\(\forall j \in [1, 2], f_{i + j} := \min\{f_{i +j1}, f_i + |a_i - a_j|\}\)。复杂度 \(\mathcal O(n)\)。
Frog 2
呱呱可以从 \(i\) 跳到 \(\forall j \in [1, k], i + j\),花费 \(|a_i - a_j|\)。求从 \(1\) 到 \(n\) 的最小花费和。
\(k \leq 100\)。
直接转移,\(\forall j \in [1, k], f_{i + j} := \min\{f_{i +j1}, f_i + |a_i - a_j|\}\)。复杂度 \(\mathcal O(kn)\)。
打家劫舍 / 没有上司的舞会
这个倒不是 atcoder 上的,山猪哥哥推荐我写的。
- https://leetcode.cn/problems/house-robber/
- https://leetcode.cn/problems/house-robber-ii/ (环形,直接做 \([0, n - 1), [1, n)\) 即可)
- http://bailian.openjudge.cn/ss2023jsj/E/ 连续三个,可惜这个不能提交。
给一个数组,选择其中的一些数使得和最大。不能选连续两个。
直接 dp,\(f_{i, j}\) 表示 \(i\) 这个元素是第 \(j\) 个连续选择的数时对应的最大答案,有:
- \(f_{i, 0} = \max\{f_{i - 1, 0}, f_{i - 1, 1}\}\)
- \(f_{i, 1} = f_{i - 1, 0} + \mathcal{nums}_i\)
展开代码
class Solution {
public:
int rob(vector<int>& nums) {
const int n = nums.size();
std::vector<std::array<int, 2>> f(n);
f[0][0] = 0;
f[0][1] = nums[0];
for (int i = 1; i < n; i++) {
f[i][0] = std::max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + nums[i];
}
return std::max(f.back()[0], f.back()[1]);
}
};
二叉树版本
class Solution {
public:
int rob(TreeNode* root) {
auto ans = [&, dfs{[&](auto &&self, TreeNode *root) -> std::array<int, 2> {
if (!root) return {};
auto l = self(self, root->left);
auto r = self(self, root->right);
return std::array<int, 2>{
std::max(l[0], l[1]) + std::max(r[0], r[1]),
root->val + l[0] + r[0]
};
}}]{
return dfs(dfs, root);
}();
return std::max(ans[0], ans[1]);
}
};
顺便交一下没有上司的舞会
#include <bits/stdc++.h>
using ll = long long;
const int N = 6010;
int n, h[N], _cnt, d[N], f[N][2];
struct edge {
int f, t;
} edges[N * 2];
void link(int u, int v) {
edges[++_cnt] = { v, h[u] }, h[u] = _cnt;
}
void dfs(int u, int p) {
f[u][1] = d[u];
for (int i = h[u]; i; i = edges[i].t) {
int v = edges[i].f;
if (v != p) {
dfs(v, u);
f[u][0] += std::max(f[v][0], f[v][1]);
f[u][1] += f[v][0];
}
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", d + i);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d%d", &u, &v);
link(u, v), link(v, u);
}
dfs(1, 0);
printf("%d\n", std::max(f[1][0], f[1][1]));
return 0;
}
剩下的明天写。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号