一类路径计数

话说今天运气还不错。开盖再来一瓶送可乐的活动连中了三瓶，请队友恰了一元可乐 (╹ڡ╹ )。

严格次小生成树

Exp++

同次小生成树，不过需要维护最大和次大，直接倍增爬。注意判自环。

展开代码

~~当然也可以在 Kruskal 重构树的欧拉序上建立主席树来求。~~

#include <bits/stdc++.h>

using ll = long long;

const int N = 100010;

int n, m, _cnt, h[N];

struct edge {
    int f, w, t, used;
    bool operator< (const edge &_) const {
        return w < _.w;
    }
} edges[N * 3], ng[N * 2];

void link(int u, int v, int w) {
    ng[++_cnt] = { v, w, h[u], 0 }, h[u] = _cnt;
}

int p[N];
int find(int x) {
    return p[x] = p[x] == x ? x : find(p[x]);
}

int t, f[N][20], dep[N], maxx[N][20], smax[N][20];

void dfs(int u, int p) {
    dep[u] = dep[f[u][0] = p] + 1;
    for (int i = h[u]; i; i = ng[i].t) {
        if (int v = ng[i].f; v != p) {
            maxx[v][0] = ng[i].w;
            dfs(v, u);
        }
    }
}

int lca(int x, int y) {
    if (dep[x] < dep[y]) std::swap(x, y);
    for (int i = t; ~i; i--) if (dep[f[x][i]] >= dep[y]) x = f[x][i];
    if (x == y) return x;
    for (int i = t; ~i; i--) if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
    return f[x][0];
}

int getMax(int x, int y, int max) {
    int ans = 0;
    for (int i = t; ~i; i--) {
        if (dep[f[x][i]] >= dep[y]) {
            ans = std::max(ans, (max != maxx[x][i] ? maxx : smax)[x][i]);
            x = f[x][i];
        }
    }
    return ans;
}

int main() {
    scanf("%d%d", &n, &m);

    t = std::__lg(n) + 1;

    for (int i = 1; i <= m; i++) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        edges[i] = { u, w, v, 0 };
    }
    
    std::iota(p, p + n + 1, 0);

    ll ans = 0;
    std::sort(edges + 1, edges + m + 1);
    for (int i = 1, cnt = 0; i <= m; i++) {
        int u = edges[i].f, v = edges[i].t, w = edges[i].w;
        int fu = find(u), fv = find(v);
        if (fu != fv) {
            ans += w;
            cnt += 1;
            link(u, v, w);
            link(v, u, w);
            p[fv] = fu;
            edges[i].used = 1;
        }
        if (cnt == n - 1) break;
    }

    dfs(1, 0);

    for (int j = 1; j <= t; j++) {
        for (int i = 1; i <= n; i++) {
            int p = f[i][j - 1];
            f[i][j] = f[p][j - 1];
            maxx[i][j] = std::max(maxx[i][j - 1], maxx[p][j - 1]);
            smax[i][j] = std::max(smax[i][j - 1], smax[p][j - 1]);
            if (maxx[i][j - 1] > maxx[p][j - 1])
                smax[i][j] = std::max(smax[i][j], maxx[p][j - 1]);
            else if (maxx[i][j - 1] < maxx[p][j - 1])
                smax[i][j] = std::max(smax[i][j], maxx[i][j - 1]);
        }
    }

    ll res = LLONG_MAX;
    for (int i = 1; i <= m; i++) {
        int u = edges[i].f, v = edges[i].t, w = edges[i].w;
        if (!edges[i].used) {
            int _lca = lca(u, v);
            int _max = getMax(u, _lca, w);
            int _sam = getMax(v, _lca, w);
            // `_max` == `_sam` iff it's on loops
            if (int x = std::max(_max, _sam); x <= w && _max != _sam) {
                res = std::min(res, ans - x + w);
            }
        }
    }

    std::cout << res << '\n';

    return 0;
}

贪心一例

中途看到群友在讨论一个题，挺简单的。

给 \(n\) 个长度为 \(m\) 的数组，从每个数组中取一个数加起来，放入数组 \(\{A\}\)，求 \(\{A\}\) 的第 \(k\) 小数。

\(n, m, k \leq 200\)。

注意到数据很小，暴力合并维护一个 \(k\) 大的堆即可，大概是个什么 \(\mathcal O(nmk \log(mk))\)，好像也不用 \(\log m\)，不过加在真数上无伤大雅。

[HNOI2006] 公路修建问题

https://www.luogu.com.cn/problem/P2323

\(n\) 个点 \(m\) 条边，两种边权 \(w_1, w_2\,(w_1 \geq w_2)\) 分别表示修建一级公路和二级公路的花费，要求至少修 \(k\) 条一级公路，问最小花费下，花费最大的那条公路的最小花费，以及总共要修建的 \(n - 1\) 条公路是哪些。

\(n \leq 10^4; m \leq 2 \times 10^4\)。

明显 \(k\) 条最小代价的一级公路，再按照 \(w_2\) 排序，从剩下的边里面选二级公路。

展开代码

#include <bits/stdc++.h>

using ll = long long;

const int N = 100010;
int n, m, k;

struct edge {
    int u, v, w1, w2, used, id;
    bool operator< (const edge &_) const {
        return w1 != _.w1 ? w1 < _.w1 : w2 < _.w2;
    }
} edges[N];

bool cmp(const edge &a, const edge &b) {
    return a.w2 < b.w2;
}

std::map<int, int> ans;

int p[N];
int find(int x) {
    return p[x] = p[x] == x ? p[x] : find(p[x]);
}

int main() {
    scanf("%d%d%d", &n, &k, &m);
    m -= 1;
    
    for (int i = 1; i <= m; i++) {
        int u, v, w1, w2;
        scanf("%d%d%d%d", &u, &v, &w1, &w2);
        edges[i] = { u, v, w1, w2, false, i };
    }
    
    std::sort(edges + 1, edges + m + 1);
    std::iota(p, p + n + 1, 0);
    
    int res = 0;
    int tot = 0;
    for (int i = 1; i <= m; i++) {
        int u = edges[i].u, v = edges[i].v;
        int w1 = edges[i].w1;
        int id = edges[i].id;
        int &used = edges[i].used;
        int fu = find(u), fv = find(v);
        if (fu != fv) {
            p[fv] = fu;
            used = true;
            res = std::max(res, w1);
            tot += 1;
            ans[id] = 1;
        }
        if (tot == k) break;
    }

    std::sort(edges + 1, edges + m + 1, cmp);
    for (int i = 1; i <= m; i++) {
        int u = edges[i].u, v = edges[i].v;
        int w2 = edges[i].w2;
        int id = edges[i].id;
        int &used = edges[i].used;
        int fu = find(u), fv = find(v);
        if (!used) {
            if (fu != fv) {
                p[fv] = fu;
                used = true;
                res = std::max(res, w2);
                tot += 1;
                ans[id] = 2;
            }
            if (tot == n - 1) break;
        }
    }
    
    printf("%d\n", res);
    for (auto [k, v] : ans) {
        std::cout << k << " " << v << '\n';
    }
    
    return 0;
}

[HAOI2006] 旅行

https://www.luogu.com.cn/problem/P2502

\(n\) 个点 \(m\) 条带权 \(w_i\) 边，找出 \(s\) 到 \(t\) 的一条路径使得这条路径上的 \(\dfrac{\max\{w_i\}}{\min\{w_i\}}\) 最小。以既约分数输出这个值或报告不连通。

\(n \leq 500; m \leq 5 \times 10^3\)。

数据很小，考虑枚举。根据题目 P1396 营救的启示，跑 Kruskal 过程中首个使得 \(s\) 与 \(t\) 联通的边权就是两点之间的最小瓶颈路。从小到大枚举分母，找到最小瓶颈路最为分子，就能最小化这个比值。然后就是愉快的 \(\mathcal O(m ^ 2 )\) 实现了~

展开代码

欢迎收看笨逼之 —— 分数初始化为 \(1\)：

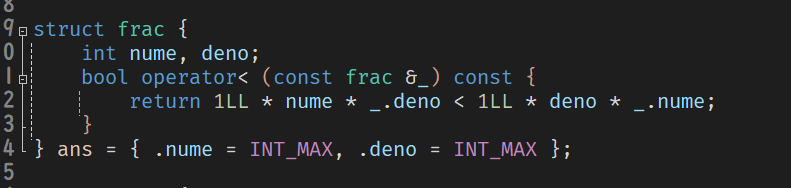
#include <bits/stdc++.h>

using ll = long long;

const int N = 510, M = 30010;

int n, m, s, t;

struct frac {
    int nume, deno;
    bool operator< (const frac &_) const {
        return 1LL * nume * _.deno < 1LL * deno * _.nume;
    }
} ans = { .nume = INT_MAX, .deno = 1 };

struct edge {
    int u, v, w;
    bool operator< (const edge &_) const {
        return w < _.w;
    }
} edges[M];

int p[N];

void reset() {
    std::iota(p, p + n + 1, 0);
}

int find(int x) {
    return p[x] = p[x] == x ? x : find(p[x]);
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v, w; i <= m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        edges[i] = { u, v, w };
    }
    scanf("%d%d", &s, &t);
    
    std::sort(edges + 1, edges + m + 1);
    
    for (int i = 1; i <= m; i++) {
        reset();
        frac res = { .nume = 0, .deno = edges[i].w };
        for (int j = i; j <= m; j++) {
            int u = edges[j].u, v = edges[j].v, w = edges[j].w;
            int fu = find(u), fv = find(v);
            if (fu != fv) {
                p[fv] = fu;
            }
            if (find(s) == find(t)) {
                res.nume = w;
//                std::cout << "! " << res.nume << " " << res.deno << '\n';
                ans = std::min(ans, res);
                break;
            }
        }
    }
    
    if (ans.nume == INT_MAX) {
        std::cout << "IMPOSSIBLE\n";
    } else if (ans.nume % ans.deno == 0) {
        printf("%d\n", ans.nume / ans.deno);
    } else {
        int gcd = std::gcd(ans.deno, ans.nume);
        printf("%d/%d\n", ans.nume / gcd, ans.deno / gcd);
    }

    return 0;
}

[AHOI2008] 紧急集合 / 聚会

https://www.luogu.com.cn/problem/P4281

\(n\) 个点的树，多次询问三点集合的最小距离和以及这个集合点。

\(n, m \leq 5 \times 10^5\)

如果是两个人集合，那么答案是他们的 \(\mathop{lca}\)；三个人时，先考虑答案会不会退化：

三个相同：选择当前点即可。
两个相同：退化为两个不同点的情况。
三个点 \(u, v, x\) 都不同：注意到 \(\mathop{lca}(u, v), \mathop{lca}(u, x), \mathop{lca}(v, x)\) 三者中必有两者相同，~~由于本题不带权~~ （不论带不带权）不同的那点必为集合点。

总之，答案为

\[dep_u + dep_v + dep_x - (dep_o + dep_p + dep_q) \]

其中 \(o, p\) 和 \(q\) 表示 \(\mathop{lca}(u, v), \mathop{lca}(u, x), \mathop{lca}(v, x)\)。

展开代码

#include <bits/stdc++.h>

using ll = long long;

const int N = 500010;
int n, m, t, h[N], _cnt, dep[N], f[N][20];

struct edge {
    int f, t;
} edges[N * 2];

void link(int u, int v) {
    edges[++_cnt] = { v, h[u] }, h[u] = _cnt;
}

void dfs(int u, int p) {
    dep[u] = dep[f[u][0] = p] + 1;
    for (int i = 1; i <= t; i++) f[u][i] = f[f[u][i - 1]][i - 1];
    for (int i = h[u]; i; i = edges[i].t) if (int v = edges[i].f; v != p) dfs(v, u);
}

int lca(int x, int y) {
    if (dep[x] < dep[y]) return lca(y, x);
    for (int i = t; ~i; i--) if (dep[f[x][i]] >= dep[y]) x = f[x][i];
    if (x == y) return x;
    for (int i = t; ~i; i--) if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
    return f[x][0];
}

int main() {
    scanf("%d%d", &n, &m);
    t = std::__lg(n) + 1;
    
    for (int i = 1, u, v; i < n; i++) {
        scanf("%d%d", &u, &v);
        link(u, v);
        link(v, u);
    }
    
    dfs(1, 0);
    
    while (m --) {
        int u, v, x;
        scanf("%d%d%d", &u, &v, &x);
        
        int o = lca(u, v);
        int p = lca(u, x);
        int q = lca(v, x);

        int ans = dep[u] + dep[v] + dep[x] - (dep[o] + dep[p] + dep[q]);
        printf("%d %d\n", o ^ p ^ q, ans);
    }
    
    return 0;
}

一类统计所有路径信息的计数问题

接下来是一类树上计数问题，说起来这个技术还是从 [HAOI2015] 树上染色学到的。 ~~不过这本身也不是特别简单的题~~

反正就是，直接求任意两点的距离什么的复杂度看起来就下不去。但如果对每一条边统计其贡献就很好做。

树上任两点距离和

https://ac.nowcoder.com/acm/contest/992/J

展开代码

超自信打了一个然后（心脏骤停）：

后来发现是写错了一个字符

#include <bits/stdc++.h>

using ll = long long;

const int N = 100010, mod = 1000000007;

int n, _cnt, h[N];

struct edge {
    int f, w, t;
} edges[N * 2];

void link(int u, int v, int w) {
    edges[++_cnt] = { v, w, h[u] }, h[u] = _cnt;
}

int s[N];

ll ans = 0;

void dfs(int u, int p) {
    s[u] = 1;
    for (int i = h[u]; i; i = edges[i].t) {
        if (int v = edges[i].f; v != p) {
            dfs(v, u);
            s[u] += s[v];
            ans = (ans + 1LL * edges[i].w * s[v] * (n - s[v]) % mod) % mod;
        }
    }
}

int main() {
    scanf("%d", &n);
    for (int i = 1, u, v, w; i < n; i++) {
        scanf("%d%d%d", &u, &v, &w);
        link(u, v, w), link(v, u, w);
    }
    
    dfs(1, 0);
    printf("%lld\n", ans);
    
    return 0;
}

另一道模板

https://ac.nowcoder.com/acm/contest/897/C

和上面有点类似，不过要求是距离能被 \(3\) 整除的所有距离的和。

乍一想有点麻烦，单独从边考虑没法知道贡献。这时候就可以递推一下，如果当前选取的端点为 \(u\)，对于它的子节点 \(v\)，需要寻找加起来模三余 \(0\) 的，即：

\[\sum_{u \in [1, n]} \sum_{j \in [0, 3)} f_{u, j} \sum_{v \in \{u\}} f_{v, 3 - j} \]

然后一直递推下去即可，很有 DAG 的感觉。

\[f_{u, j} = f_{u, j} + f_{v, (j + w) \bmod 3} \]

核心代码

ll ans = 0, f[N][3];

void dfs(int u, int p) {
    f[u][0] = 1;
    for (int i = h[u]; i; i = edges[i].t) {
        if (int v = edges[i].f, w = edges[i].w; v != p) {
            dfs(v, u);
            for (int j = 0; j < 3; j++) {
                ans += 1LL * f[u][j] * f[v][(3 - j - w + 3) % 3];
            }
            for (int j = 0; j < 3; j++) {
                f[u][(j + w) % 3] += f[v][j];
            }
        }
    }
}

posted @ 2023-04-13 00:36 PatrickyTau 阅读(29) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

Patricky

20230412 训练记录：最小生成树 / lca / 一类路径计数

严格次小生成树

贪心一例

[HNOI2006] 公路修建问题

[HAOI2006] 旅行

[AHOI2008] 紧急集合 / 聚会

一类统计所有路径信息的计数问题

树上任两点距离和

另一道模板

公告