20230411 训练记录:lca / 次小生成树
先打了个 lca 板子,POJ1330,要找一下根:
for (int i = 1, u, v; i < n; i++) {
scanf("%d%d", &u, &v);
link(u, v), link(v, u);
d[v] += 1;
}
int rt = 1; while (d[rt]) rt += 1;
dfs(rt, 0);
中途去搞了很久学校的事情
哦,真无语,中途去搞了好久 OJ。学校服务器批下来了,但是是古老的 centOS。你偌大个双一流高校用这种古董玩意,真的很下头。Hydro 因为 centOS 没给最新的 cgroup 用不了。HUSTOJ 也是因为 centOS 不能判题。😅 太失望了。
反正忙一下午都没整出个结果来,完全不懂 centOS。要不最后搭一个 qduoj 差不多得了。
然后还有个小组作业,另外两个同学都想让我做。小组作业什么时候滚出大学教学啊?
树边,前向边,后向边,横叉边
对图进行 dfs 会得到一棵 dfs 树(或森林),在这个树上有如下几种边。

dfs 树不存在前向边和横叉边。
唯一 MST / 次小生成树
- http://poj.org/problem?id=1679
- https://www.acwing.com/problem/content/4339/
- https://www.acwing.com/problem/content/4357/
判断一张图是否有唯一的最小生成树。
- \(n \leq 10^4, m \leq 10^6\)。
一个朴素的想法是,求出最小生成树和次小生成树,再判断它们是否相同。问题转换为如何求解次小生成树,从 Kruskal 的贪心性质来看,在某个局部放弃最优解而选择次优解就可以求得答案。
朴素实现是 \(\mathcal O(m^2 \log m)\) 的,考虑到对于每条加入的非树边都会新增一个环,要替换的其实就是最大边权,求最小生成树上两点之间的最大边权可以使用昨天学到的 Kruskal 重构树。当然 POJ 这题 \(m\) 不大,可以使用 \(\log n\) 的倍增来求。
打了 Kruskal 重构树居然 T 了,不清楚哪里写挂了 T_T, 中途写挂了一个点,重新打了一遍终于在凌晨三点过了 qwq。
展开代码
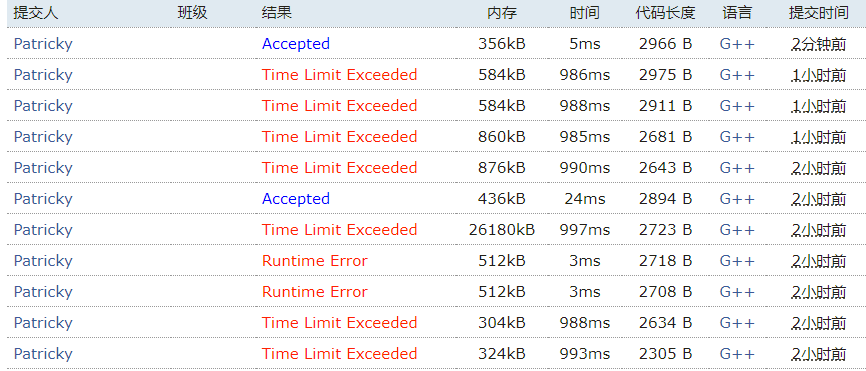
#include <bits/stdc++.h>
int main() {
// std::cin.tie(nullptr)->sync_with_stdio(false);
int t;
std::cin >> t;
void solve();
while (t --)
solve();
return 0;
}
void solve() {
int n, m;
std::cin >> n >> m;
std::vector<std::tuple<int, int, int, int>> edges(m);
for (auto &[w, u, v, used] : edges) {
std::cin >> u >> v >> w;
used = 0;
}
std::sort(edges.begin(), edges.end());
std::vector<int> p(n * 3);
std::iota(p.begin(), p.end(), 0);
std::function<int(int)> find = [&p, &find](int x) -> int {
return p[x] = p[x] == x ? p[x] : find(p[x]);
};
int ans = 0, cnt = n, tot = 0;
std::vector<std::vector<int>> g(2 * n + 1);
std::vector<int> d(n * 2 + 1, 0);
for (auto &[w, u, v, used] : edges) {
int x = find(u), y = find(v);
if (x != y) {
d[++cnt] = w;
p[x] = p[y] = p[cnt] = cnt;
g[cnt].push_back(x), g[x].push_back(cnt);
g[cnt].push_back(y), g[y].push_back(cnt);
ans += w;
tot += 1;
used = true;
}
if (tot == n - 1) break;
}
// for (int i = 1; i <= n * 2; i++) {
// for (int j : g[i])
// std::cout << i << " " << j << '\n';
// }
//
// std::cout << '\n';
// for (int i = n + 1; i <= n * 2; i ++)
// std::cout << d[i] << " ";
std::vector<std::vector<std::pair<int, int>>> q(n + 1);
for (int i = 0; i < m; i++) {
auto [w, u, v, used] = edges[i];
if (!used) {
q[u].emplace_back(v, i);
q[v].emplace_back(u, i);
}
}
std::vector<int> res(m, 0), st(cnt + 1, 0);
std::function<void(int, int)> tarjan = [&](int u, int fa) -> void {
st[u] = 1;
for (auto v : g[u]) if (v != fa) {
tarjan(v, u);
int x = find(u), y = find(v);
if (x != y)
p[y] = x;
}
// std::cout << "?? u = " << u << '\n';
if (u <= n) { // 是这里挂了!
/*
q 的查询在 [1, n] 但是跑的 dfs 是在 kruskal 重构树上,所以会到 [1, 2n)
太粗心了
*/
for (auto [v, i] : q[u]) {
// std::cout << "! v = " << v << ", i = " << i << '\n';
if (st[v] == 2) {
int lca = find(v);
res[i] = d[lca];
}
}
}
st[u] = 2;
};
std::iota(p.begin(), p.end(), 0);
tarjan(cnt, 0);
int sna = INT_MAX;
for (int i = 0; i < m; i++) {
auto [w, u, v, used] = edges[i];
if (!used) {
// std::cout << "! res[" << i << "] = " << res[i] << '\n';
sna = std::min(sna, ans + w - res[i]);
}
}
// std::cout << "! " << sna << '\n';
if (ans == sna)
std::cout << "Not Unique!\n";
else
std::cout << ans << '\n';
}
树的直径(复习)
给一棵树,要求建立 \(n - 1\) 条 “新边”,“新边” 的边权为原图两点间的距离,求最大 “新边” 边权和。
可见至少得先选直径 \(d_1, d_2\),随后按照 \(\max\{\operatorname{dist}(d_1, i), \operatorname{dist}(d_2, i)\}\) 连边,用三次 dfs 即可得出需要的信息。
展开代码
#include <bits/stdc++.h>
using ll = long long;
int main() {
std::cin.tie(nullptr)->sync_with_stdio(false);
int n;
while (std::cin >> n) {
std::vector<std::vector<std::pair<int, ll>>> g(n + 1);
for (int i = 1, u, v, w; i < n; i++) {
std::cin >> u >> v >> w;
g[u].emplace_back(v, w);
g[v].emplace_back(u, w);
}
std::array<std::vector<ll>, 2> dist;
int d = -1;
ll ans = 0;
for (int t : {0, 1}) {
dist[t] = std::vector<ll>(n + 1);
}
std::function<void(int, int, ll, int, int)> dfs = [&](int u, int p, ll weight, int t, int f) -> void {
if (weight > ans) ans = weight, d = u;
for (auto [v, w] : g[u]) if (v != p) {
if (f) dist[t][v] = dist[t][u] + w;
dfs(v, u, w + weight, t, f);
}
};
dfs(1, 0, 0, 0, 0);
dfs(d, 0, 0, 0, 1);
dfs(d, 0, 0, 1, 1);
ans *= -1;
for (int i = 1; i <= n; i++) {
ans += std::max(dist[0][i], dist[1][i]);
}
std::cout << ans << '\n';
}
return 0;
}
多个点的 lca
多次询问下标在 \([l, r]\) 之间的所有点的 \(\mathop{lca}\)。
\(n, q \leq 3\times10^5\)
ML: \(128 \rm Mib\)
结论:多个点的 \(\mathop{lca}\),是 dfs 序最小最大的两个节点的 \(\mathop{lca}\)。
用 \(\rm ST\) 维护区间 dfs 序最小和最大,然后就变成模板题了~ 正好没背昨天学的 RMQ 求 \(\mathop{lca}\),背一下。
信心满满打完结果 wa 了... 明早再调... 改成倍增过了...
展开代码

加不加 dfn[u] = ++tag 都能过??? 逆天。
#include <bits/stdc++.h>
using ll = long long;
const int N = 300010;
int n, _cnt, h[N];
struct edge {
int f, t;
} edges[N * 2];
void link(int u, int v) {
edges[++_cnt] = { v, h[u] }, h[u] = _cnt;
}
int dfn[N], pos[N], tag;
int maxDfn[N][20];
int minDfn[N][20];
int minDfnCmp(int x, int y) {
return dfn[x] < dfn[y] ? x : y;
}
int maxDfnCmp(int x, int y) {
return x ^ y ^ minDfnCmp(x, y);
}
int (*minDfnCb)(int, int) = minDfnCmp;
int (*maxDfnCb)(int, int) = maxDfnCmp;
int f[N][20], dep[N], t;
void dfs(int u, int p) {
dfn[u] = ++tag;
dep[u] = dep[f[u][0] = p] + 1;
for (int i = 1; i <= t; i++) f[u][i] = f[f[u][i - 1]][i - 1];
for (int i = h[u]; i; i = edges[i].t) {
int v = edges[i].f;
if (v != p) {
dfs(v, u);
}
}
}
int lca(int x, int y) {
if (dep[x] < dep[y]) return lca(y, x);
for (int i = t; ~i; i--) if (dep[f[x][i]] >= dep[y]) x = f[x][i];
if (x == y) return x;
for (int i = t; ~i; i--) if (f[x][i] != f[y][i]) {
x = f[x][i];
y = f[y][i];
}
return f[x][0];
}
int query(int (*func)(int, int), int (*st)[20], int l, int r) {
int t = std::__lg(r - l + 1);
return func(st[l][t], st[r - (1 << t) + 1][t]);
}
int main() {
while (~scanf("%d", &n)) {
_cnt = tag = 0;
memset(h, 0, sizeof h);
memset(dfn, 0, sizeof dfn);
memset(f, 0, sizeof f);
memset(dep, 0, sizeof dep);
for (int i = 1, u, v; i < n; i++) {
scanf("%d%d", &u, &v);
link(u, v);
link(v, u);
}
t = std::__lg(n) + 1;
dfs(1, 0);
for (int i = 1; i <= n; i++) {
minDfn[i][0] = maxDfn[i][0] = i;
}
for (int j = 1; j <= t; j++) {
for (int i = 1, lim = 1 << (j - 1); i + lim * 2 - 1 <= n; i++) {
minDfn[i][j] = minDfnCmp(minDfn[i][j - 1], minDfn[i + lim][j - 1]);
maxDfn[i][j] = maxDfnCmp(maxDfn[i][j - 1], maxDfn[i + lim][j - 1]);
}
}
int q;
scanf("%d", &q);
while (q --) {
int l, r;
scanf("%d%d", &l, &r);
int m = query(minDfnCb, minDfn, l, r);
int M = query(maxDfnCb, maxDfn, l, r);
printf("%d\n", lca(m, M));
}
}
return 0;
}
总结
总结就是学校事真的多 😅。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号