Javascript 产生随机数——服从均匀分布随机数、服从正态分布(高斯分布)随机数、服从柯西分布随机数
1 产生服从均匀分布随机数
大家都知道Math.random是 javascript 中返回伪随机数的方法,但Math.random()产生 [0,1)区间的随机数(注意,不包括1),如果要取到1,可以这样:Math.floor(Math.random()*2);,取到 [0,2)之间的数然后向下取整,得到[0,1]。
取整数随机数要使用 floor 函数向下取整,而不能使用 round 函数四舍五入取整,round 取整后得到的是非均匀分布。
如果要取得特定范围的随机数可以对Math.random进行四则运算
例如:
//[10,20)
a=Math.random*10+10;
//[10,20]
a=Math.floor(Math.random()*11+10);
2 产生服从正态分布随机数
正态分布即高斯分布
Box-Muller变换是通过服从均匀分布的随机变量,来构建服从正态分布的随机变量的一种方法。
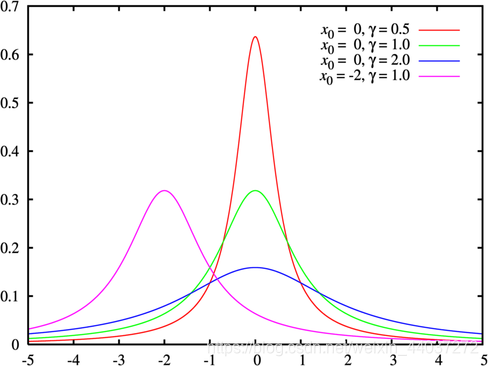
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y3a7obBH-1622166865554)(https://zh.wikipedia.org/wiki/File:Normal_Distribution_PDF.svg)]](https://img-blog.csdnimg.cn/20210528095438194.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDAzNzI3Mg==,size_16,color_FFFFFF,t_70)
function normalRandom(mean, std) {
let u = 0.0, v = 0.0, w = 0.0, c = 0.0;
do {
//获得两个(-1,1)的独立随机变量
u = Math.random() * 2 - 1.0;
v = Math.random() * 2 - 1.0;
w = u * u + v * v;
} while (w == 0.0 || w >= 1.0)
//Box-Muller转换
c = Math.sqrt((-2 * Math.log(w)) / w);
let normal = mean + (u * c) * std;
return normal;
}
//用于生产服从正态分布的随机数矩阵
function normalRandomSize(mean,std,size){
let normal = [];
for(let i=0;i<size;i++){
normal[i]=randomNormal(mean,std);
}
return normal;
}
3 产生服从柯西分布随机数
柯西分布的概率密度函数为
f
(
x
)
=
β
π
[
β
2
+
(
x
−
α
)
2
]
β
>
0
f(x)=\frac{\beta }{\pi [\beta ^{2}+ (x - \alpha)^{2}]} \qquad \beta > 0
f(x)=π[β2+(x−α)2]ββ>0
通常用
C
(
α
,
β
)
C(\alpha ,\beta )
C(α,β)表示,其分布函数为
F
(
x
)
=
1
2
+
1
π
a
r
c
t
a
n
(
x
−
α
β
)
F(x)=\frac{1}{2}+\frac{1}{\pi }arctan(\frac{x-\alpha}{\beta })
F(x)=21+π1arctan(βx−α)
用逆变换法产生柯西分布(Cauchy(\alpha ,\beta ))的随机变量(x),产生均匀分布的随机数
u
u
u,计算具体方法如下:
x
=
α
−
β
t
a
n
(
π
u
)
x=\alpha - \frac{\beta }{tan(\pi u)}
x=α−tan(πu)β
function cauchyRandom(a,b) {
let u,cauchy;
u = Math.random();
cauchy = a - b / Math.tan(Math.PI * u);
return cauchy;
}
本文来自博客园,作者:Patrick-Rex,转载请注明原文链接:https://www.cnblogs.com/patrickrex/p/18028809


 浙公网安备 33010602011771号
浙公网安备 33010602011771号