数学建模之求解微分方程和差分方程
求微分方程的解
自牛顿发明微积分以来,微分方程在描述事物运动规律上已发挥了重要的作用。实际应用问题通过数学建模所得到的方程,绝大多数是微分方程。由于实际应用的需要,人们必须求解微分方程。然而能够求得解析解的微分方程十分有限,绝大多数微分方程需要利用数值方法来近似求解。下面介绍如何用 Matlab 来计算微分方程(组)的数值解。
Euler折线法
微分方程的基本数值解法——Euler折线法。
步骤:
分割求解区间,差商代替微商,解代数方程
例子:
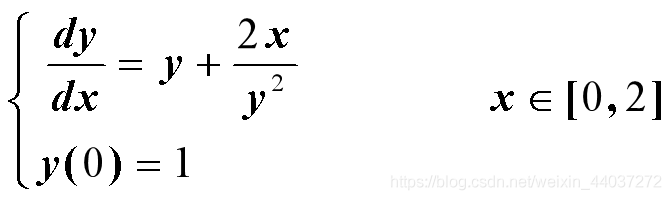 解:
解:
等距剖分: a = x 0 < x 1 < x 2 < ⋯ < x n − 1 < x n = b a=x_0<x_1<x_2< \cdots <x_{n-1}<x_n=b a=x0<x1<x2<⋯<xn−1<xn=b
步长: h = x k + 1 − x k = ( b − a ) / n , k = 0 , 1 , 2 , . . . , n − 1 h=x_{k+1}-x_k=(b-a)/n,k=0,1,2,...,n-1 h=xk+1−xk=(b−a)/n,k=0,1,2,...,n−1
y ( x k + 1 ) ≈ y ( x k ) + h y ′ ( x k ) y(x_{k+1})\approx y(x_k)+hy\prime(x_k) y(xk+1)≈y(xk)+hy′(xk)
取步长 h = (2 - 0)/n = 2/n,得差分方程
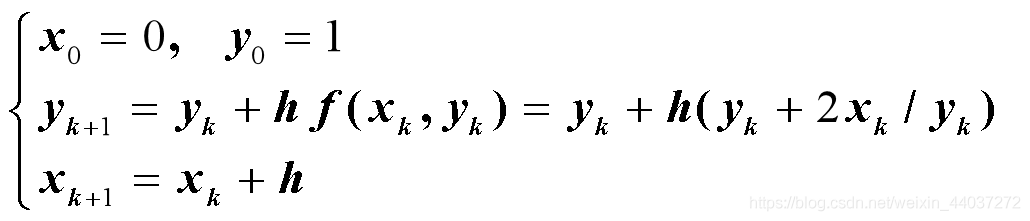
当 h=0.4,即 n=5 时,代码如下:
clear
a=0; b=2;
h=0.4;
n=(b-a)/h+1;
x(1)=0; y(1)=1;
for i=1:n-1
y(i+1)=y(i)+h*(y(i)+2*x(i)/y(i)^2);
x(i+1)=x(i)+h;
end
y1=((5/3)*exp(3*x)-2*x-2/3).^(1/3);
plot(x,y1,x,y);
h = legend('解析解','Euler解');
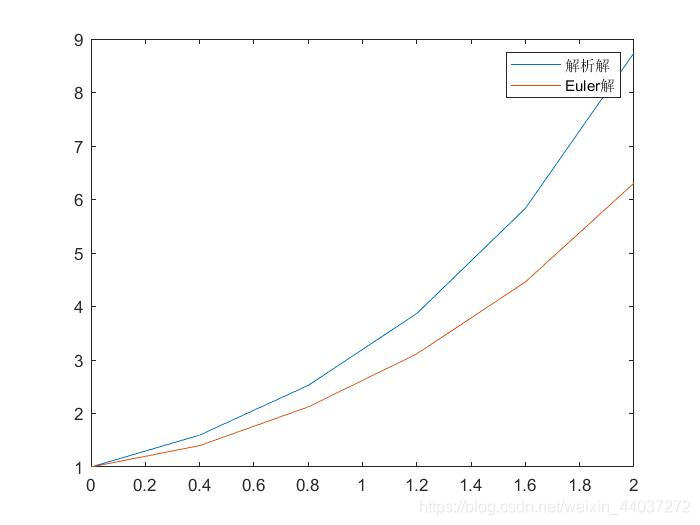
解得:
y
=
(
5
3
e
3
x
−
2
x
−
2
3
)
1
/
3
y=(\frac{5}{3}e^{3x}-2x-\frac{2}{3})^{1/3}
y=(35e3x−2x−32)1/3
Runge-Kutta方法
龙格-库塔法(Runge-Kutta methods)是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。
同样是上面的例子:

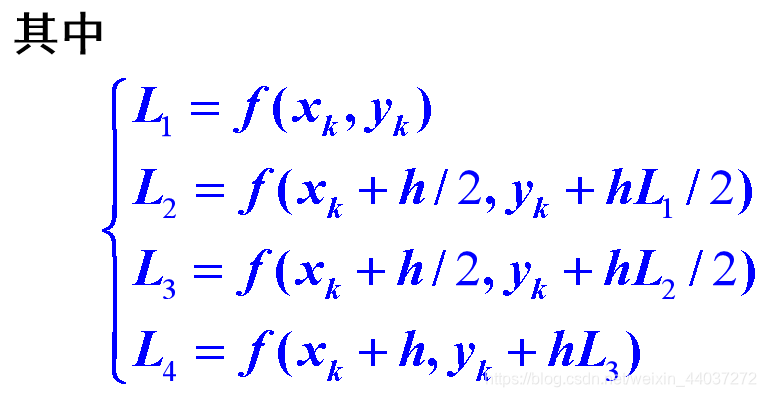
clear;
a=0; b=2; h=0.4;
n=(b-a)/h+1;
x(1)=0; y(1)=1;
for i=1:n-1
L1=y(i)+2*x(i)/y(i)^2;
t=x(i)+h/2;t1=y(i)+h*L1/2;
L2=t1+2*t/t1^2;t1=y(i)+h*L2/2;
L3=t1+2*t/t1^2;t1=y(i)+h*L3/2;
L4=t1+2*(x(i)+h)/t1^2;
y(i+1)=y(i)+h*(L1+2*L2+2*L3+L4)/6;
x(i+1)=x(i)+h;
end
plot(x,y)

MATLAB自带的ODE求解器
ODE (常微分方程)
没有一种算法可以有效地解决所有的 ODE 问题,因此MATLAB 提供了多种ODE求解器,对于不同的ODE,可以调用不同的求解器。

基本语法
[T,Y] = solver(odefun,tspan,y0)
其中 y0 为初值条件,tspan为求解区间;Matlab在数值求解时自动对求解区间进行分割,T (向量) 中返回的是分割点的值(自变量),Y (向量) 中返回的是解函数在这些分割点上的函数值。
solver 为Matlab的ODE求解器(可以是 ode45、ode23、ode113、ode15s、ode23s、ode23t、ode23tb)
上一篇:数学建模基础知识
下一篇:
本文来自博客园,作者:Patrick-Rex,转载请注明原文链接:https://www.cnblogs.com/patrickrex/p/18028791


 浙公网安备 33010602011771号
浙公网安备 33010602011771号