二叉搜索树(Binary-Search-Tree)--BST
要求:AVL树是BBST的一个种类,继承自BST,对于AVL树,不做太多掌握要求
- 四种旋转,旋转是BBST自平衡的基本,变换,主要掌握旋转的思想。
- 3+4重构,重点明白为什么可以3+4重构,而不是使用旋转
- 对于AVL插入和删除做了解,知道其为什么比不过红黑树就可以了。
循关键码访问(call-by-key)
- 关键码:就是所谓的key
- 条件:
- 关键码之间支持大小比较
- 支持相等比对
- 在BST中,所有数据都统一实现和表示为entry(entry是什么?)
entry(词条)其实就是(key-value)对
同时还支持大小比较和相等比对(通过比较词条的key)的方式。
概念
- 词条,二叉树的节点,关键码三者之间在不做具体强调的时候,概念等同。
BST特征
- 顺序性:任意节点均不小于其左后代。且其右后代也均不小于其节点。
- 数学语言描述就是
one-of-left-node <= V <= one-of-right-node - 注意这里是
后代,不是孩子
- 数学语言描述就是
- 简化条件:禁止重复词条, 意识就是目前不考虑重复key的存在
- 经过简单扩容后就可以支持重复词条。
- BST的中序遍历必然单调。因此就得到了
判断树是否是BST的方法。
注意key-value的映射为单一映射,不存在单一key映射多个value,但不同key可以映射相同value,具体
设计看自己
接口
查找 search
search查找的本质就是二分查找。
BST<T>::searchIn(BinNodePos(T) &v , const T &key, BinNodePos(T) &hot /*记忆热点*/)
{
if(!v || (key == v->data)) return v;
hot = v;
return searchIn(( key < v->data ? v->lc : v->rc), key, hot);
- 代码本身没有难度,这里主要注重接口语义:
- hot的语义: 查找成功时,返回命中节点的父亲。 查找失败时,返回最后返回的一个存在的非空节点。
- 语义统一: 假设我们在查找失败的时候引入假想的哨兵节点,且其key值正好等于我们要找的key。则search
返回的就是目标节点。hot返回的就是目标节点的父亲。 - 注意返回值,和第一个参数,都是使用的指针的引用。这样做的目的是让search的返回值后续被其他接口
调用,而且主需要改变这个返回值,就可以改变指针的指向,所以指针配合引用的方式取缔了二级指针的使用,
熟悉了后,感到很方便。
- hot的语义: 查找成功时,返回命中节点的父亲。 查找失败时,返回最后返回的一个存在的非空节点。
插入 insert
再次重申,我们当前认为不存在重复节点。那么,我们要插入的元素,通过search(e)接口的调用,
就会发现返回的位置恰好就是我们当初假想的哨兵。也就是e应该存在的位置。
那么就很简单了, 直接操作返回位置。就可以了。
现在明白为什么当初返回的是BinNodePos(T) & 了。
BinNodePos(T)
BST<T>::insert(const T &e)
{
BinNodePos(T) x = search(e);
if(!x) // 保证插入元素不存在
{
x = new BinNode(e, _hot); // 很方便的完成了parent的回指,
/* ----- 要记得维护该有的数据项 ----- */
++_size;
updateHeightAbove(_hot); // 从插入节点的父亲节点开始更新高度,逐步向上
}
return x;
}
有些数据结构时不维护height的,但是接下使用的AVL树需要使用height
删除 remove
删除同插入一样,在删除之后,依然要保持这个BST的有序性。而且同样需要维护height和size。
因此,删除比较复杂的情况在于删除目标元素后,目标元素后面的元素有一个替换的过程。
bool remove(const T &e)
{
BinNodePos(T) x = search(e);
if(!x) return false;
removeAt(x, _hot);
--_size;
updateHeightAbove(_hot);
return true;
}
void removeAt(BinNodePos(T) &x, BinNodePos(T) &hot)
{
BinNodePos(T) w = x; // 保存删除节点位置
BinNodePos(T) succ = nullptr;
if(!x->lc && !x->rc)
{
// do nothing
}
else if(!x->lc) // 左树为空的情况下
{
succ = x = x->rc;
/* 拆开来理解
x = x->rc; 直接让删除节点的后继覆盖删除节点
succ = x; 然后然明文后继指向后继,标记后继位置
*/
}
else if(!x->rc)
{
succ = x = x->lc;
}
else{ // 哇,最喜欢这里
w = w->succ(); // w指向自己的中序后继, 这里要从中序遍历的序列理解,删除一个树的节点,
// 我们先将这个树的值和其中序遍历后继替换再删,就是相当于交换了有序的向量 的下一个值,然后删下
// 个值,没有任何影响,但是这个节点的中序遍历后继最多只可能有一个孩子, 因为当前节点左右孩子
// 都有,那么其后继一定在右孩子中的最左分支。那么其就不能有右孩子。最多只能有一个右孩子。
std::swap(w->data, x->data);
// 到目前为止,w依然保留着删除节点位置(虽然它动了)
BinNodePos(T) u = w->parent;
if(u == x) // 即使w->rc为nullptr也没关系
u->rc = succ = w->rc;
else
u->lc = succ = w->rc
}
hot = w->parent;
if(succ) succ->parent = hot; // 如果删除节点的后继存在,还要进行回指
release(w->data);
release(w);
return succ;
}
/* 只会出现俩种情况 情况1
.─.
.─. ( X )
( X ) <- u ▪ `─' ▪
▪`─'▪ ▪ ▪
▪ ▪ ▪ ▪ .─.
▪ ▪.─. ▪ ( )
▪ ▪ ( W ) ▪ ▪`─'
▪▪▪ `─'▪ ▪ ▪ .─.▪
▪ ▪ ▪ ▪▪▪ u-> (...) ◀┐
▪ ▪ ▪ ▪ ▪ ▪`─' │ ┌────────────────┐
▪ ▪ ▪ ▪ ▪ ▪ └──│ may many nodes │
▪ ▪ ▪▪▪ ┌──────────────┐ ▪ ▪ .─.▪ └────────────────┘
▪ T ▪ ▪ ▪ ┌──│may not exist │ ▪ ▪ ( W )
▪ ▪ ▪ ▪ │ └──────────────┘ ▪ T ▪ `─'▪
▪ ▪ ▪ ▪ │ ▪ ▪ ▪
▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪ ▪ ▪ ◀─┘ ▪ ▪ ▪
▪ T ▪ ▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪ ▪
▪ ▪ ▪▪▪ ┌──────────────┐
▪ ▪ ▪ ▪ ┌──│may not exist │
▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪ ▪ ▪ │ └──────────────┘
▪ ▪ │
▪ ▪ ◀─┘
▪ T ▪
▪ ▪
▪ ▪
▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪
*/
平衡与代价
BST的所有查找,插入,删除均为O(h)的复杂度。
注意BST的高度并不是log(N);
最坏情况下是线性排列,那么h = n
这也就引入了AVL树和RB树。
理想平衡
在理想平衡下,树的高度总共不会超过logN,但是需要注意的是,维护这样一种状态,在插入和删除后进行的
状态调整代价可能会很高,因为我们寻求的是一种适度平衡。
平衡二叉搜索树 Balance-BST -- BBST
注意:对于BBST来说,仍然要保持BST的有序性,即中序遍历的序列不能发生变化。
这样俩个BST,我们称为等价BST,利用的就是中序遍历的歧义性。
等价BST变换规律:
- 上下可变: 祖先和后代关系可以发生颠倒, 在垂直方向有一定自由度
- 左右不乱: 在节点左侧的节点,经过调整后,依然在左侧,在右侧的节点经过调整后依然在右侧。
基本变换
任何BST之间的等价变换都是经过一系列的基本变换形成的。详细证明可以参考《数据结构与算法分析》
旋转操作
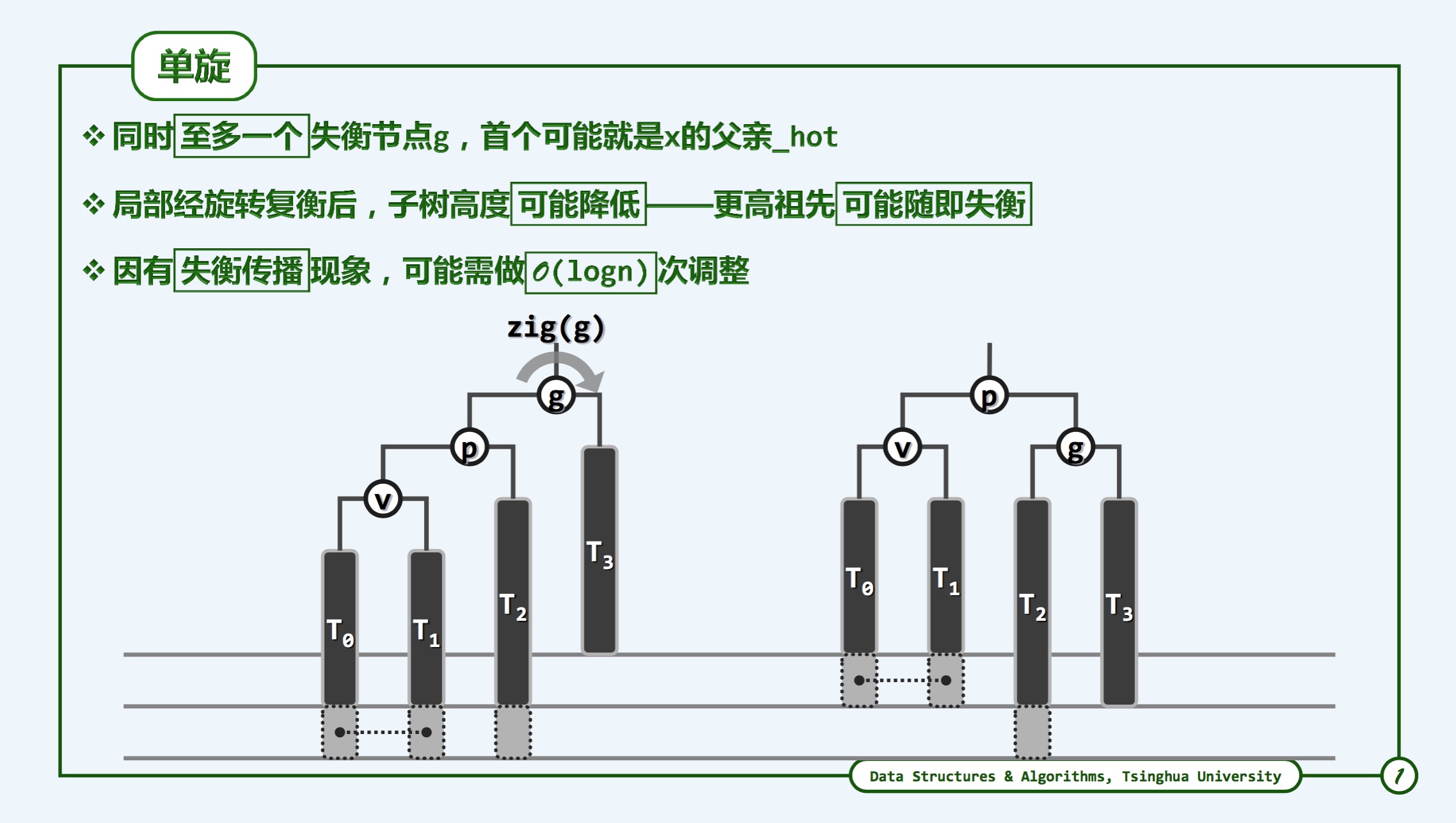
- 单旋转
俩种单旋转: - (向)右旋转——zig, (向)左旋转--zag
- 如果导致失衡,插入一定插入在较高的子树,平衡因子由原来的+1变为+2。
┌────────────────────┐ ┌────────────────────┐
│balfactor: +1 -> +2 │ │balfactor: +2 -> +1 │
└────────────────────┘ └────────────────────┘
┌────┐ .─. .─.
│ g │──────────────▶(50 ) (40 )
└────┘ ▪`─'▪ ▪`─'▪
▪ ▪ ─────────────────────▶ ▪ ▪
┌────┐ .─▪ ▪.─. .─.▪ ▪.─.
│ p │───────▶(40 ) (60 ) (35 ) (50 )
└────┘ ▪ `─'▪ `─' ▪`─' ▪`─'▪
▪ ▪ ▪ ▪ ▪
┌────┐ .─▪ .▪. ┌───────────────────┐ ▪ ▪ ▪
│ v │─▶(35 ) (45 )◀────────│ may not exist │ .─. .─. .─.
└────┘ ▫`─' `─' └───────────────────┘ (35 ) (45 ) (60 )
▫ `─' `─' `─'
▫
.─. ┌──────────────────────┐
(30 )◀────│ the new insert node │
`─' └──────────────────────┘
操作步骤:
- 首先得到一个临时的引用rc指向p
- g的左子树指向p的右子树
- 令g称为p的右孩子
- 将局部子树的根指向p,然后去掉rc
- zag左旋操作与此同理。
总的来说,单旋转呈现这么一种特性,即v,p,g分布单向,g为局部子树的根,调整完毕后,v,p,g自己可以形成
一个满树,p为局部子树的根
- 双旋转
- 此时v,p,g不再呈现一边的趋势,而是分开了。只需要执行一次zag左旋就可以达到之前的单旋转状态
┌────────────────────┐ ┌────────────────────┐
│balfactor: +1 -> +2 │ │balfactor: +2 -> +1 │
└────────────────────┘ └────────────────────┘
┌────┐ .─. .─.
│ g │──────────────▶(50 ) g-> (50 )
└────┘ ▪`─'▪ ▪`─'▪
▪ ▪ ─────────────────────▶ ▪ ▪
┌────┐ .─▪ ▪.─. .─.▪ ▪.─.
│ p │───────▶(40 ) (60 ) p-> (45 ) (60 )
└────┘ ▪ `─'▪ `─' ▪`─'▪ `─'
▪ ▪ ▪ ▪
.─▪ .▪. ▪ ▪
(35 ) ┌──▶(45 ) .─. .─.
`─' │ `─'▪ v-> (40 ) (48 )
│ ▪ ▪`─' `─'
│ ▪ ▪
┌────┐ │ .─. ┌──────────────────────┐ .─.
│ v ├─┘ (48 )◀──────│ the new insert node │ (35 )
└────┘ `─' └──────────────────────┘ `─'
- 使用rc临时引用指向v
- 让p的右子树指向v的左子树,
- 让v的左子树指向p
- 让局部子树的根指向v,并去掉rc
- 就得到可以进行单旋的状态。
让我们再次来复习下右旋。
- 让临时引用rc指向p
- 让g的左子树指向p的右子树
- 让p的右子树指向g
- 让局部子树的根指向p,并去掉rc
到此,俩类共4个旋转操作的文字说明和图示如上。接下来,看到底怎样使用基本操作将树由BST拉回BBST
具体的四种旋转,可以查看AVL的四种旋转
AVL树
AVL树是BBST的一个种类。
平衡因子:左子树的高度减去右子树的高度,
AVL树的平衡因子不会超过1。 AVL树| balFac(v) | <= 1
回忆:之前我们定义过,空树的高度为-1,有一个节点的树高度为0。
一颗树的高度,就是树中深度最大节点的深度。
可以将状态定义如下
#define BalFac(x) (stature((x).lc) - stature((x).rc)) //平衡因子
#define AvlBalanced(x) ((-2 < BalFac(x)) && (BalFac(x) < 2)) //AVL平衡条件
失衡
插入
插入一个新节点,会导致节点的所有祖先失衡。 最多logN个节点。
- 原因:插入一个新节点,会更新节点以及节点所有祖先。
- 但是插入操作反而比删除操作更为简便一些。经过一次调整就可以完成
- 特征
- 插入一个节点后,失衡节点集为新插入节点x的祖先,且高度均不低于新插入节点x的祖父。
- 这个高度最低的失衡节点我们标记为g
- g不一定是x的祖父,有可能是更高的祖先
插入重平衡
- 在x和g的通路上,我们设p为g的孩子,设置v为p的孩子。
实现:
- 找g节点:那么重平衡的关键就是首先要找到g,这个很简单,从x的parent的往上开始,找不满足avl平衡条件
的节点。 - 找p,v节点:找到g节点后,我们知道g节点是失衡的,因为新插入了x节点,那么其在通往x节点的通路上的高度
则会均大于他们的兄弟,借此,可以寻找p,v节点。其实就是找v节点就够了。p是v的parent。
宏代码如下所示,解读:
#define tallerChild(x) (\ /*说白了就是在找高度更高的孩子*
stature((x)->lc) > stature((x)->rc) ? (x)->lc : ( /*左高*/ \
stature((x)->lc) < stature((x)->rc) ? (x)->rc : ( /*右高*/ \
IsLchild(*(x)) ? (x)->lc : (x)->rc /*等高*/ \
)\
)\
)\
等高情况发生在AVL树删除的情况下, 在插入情况下不会发生。
代码如下
void insert(const T &e)
{
// 插入操作前面的代码和正常BST的插入一样
BinNodePos(T) & x = search(e);
if(x)
return ; // 目前不考虑重复元素
x = new BinNode(e, _hot); // 直接完成新节点的构建,paret指向_hot,回想之前search的语义
++_size;
BinNodePos(T) xx = x; // 接下来就是AVL树自己独有的部分
/* ------- AVL 特有部分-------- */
for(BinNodePos(T) g = xx->parent; g; g = g->parent)
{
if(!AvlBalanced(g)) // 根据g的定义找到g
{
// fromparentto返回当前节点父亲节点的指针域, 即局部子树的根引用
// 由此可推断,rotate返回的是p
FromParentTo(*g) = rotateAt(tallerChild( tallerChild(g) ));
break;
}
else{
updateHeightAbove(g); // 同时还要一步一步进行高度更新。但调整完毕后就直接退出了,
// 不需要更新了, 原因在于插入调整不会改变g的祖先的高度, 和插入前的高度保持一致
}
}
return xx;
}
效率:
可以看出,插入操作只需要执行O(logN)的查找时间,然后进行最多不超过O(logN)的平衡确认,如果失衡
执行不超过2次的旋转调整,由此AVL树的插入操作在O(logN)的时间内可以完成
删除
删除一个新节点,只会导致最多1个节点失衡。
- 原因:如果导致失衡,删除节点时,一定是删除更短的那个分支,而这个子树的高度担当还是在最长
子树那里。 - 特征
- 与插入不同的是,删除操作中失衡节点集始终最多只含有一个节点。
- 重平衡 教材P198页有详细讲解,这标记一下
- 寻找g:节点依然是按照之前的方法,通过被删除节点的parent向上查找,到不满足AVL平衡条件的那个
点 - 寻找p:作为失衡节点,其另一边的高度至少为1才能构成失衡。因此必定有一个非空的孩子p,且是
tallerchild - 寻找v:寻找v的时候,p的俩个孩子高度可能相等。此时我们优先选取和p同向者,单旋当然比双
旋简单。
- 寻找g:节点依然是按照之前的方法,通过被删除节点的parent向上查找,到不满足AVL平衡条件的那个
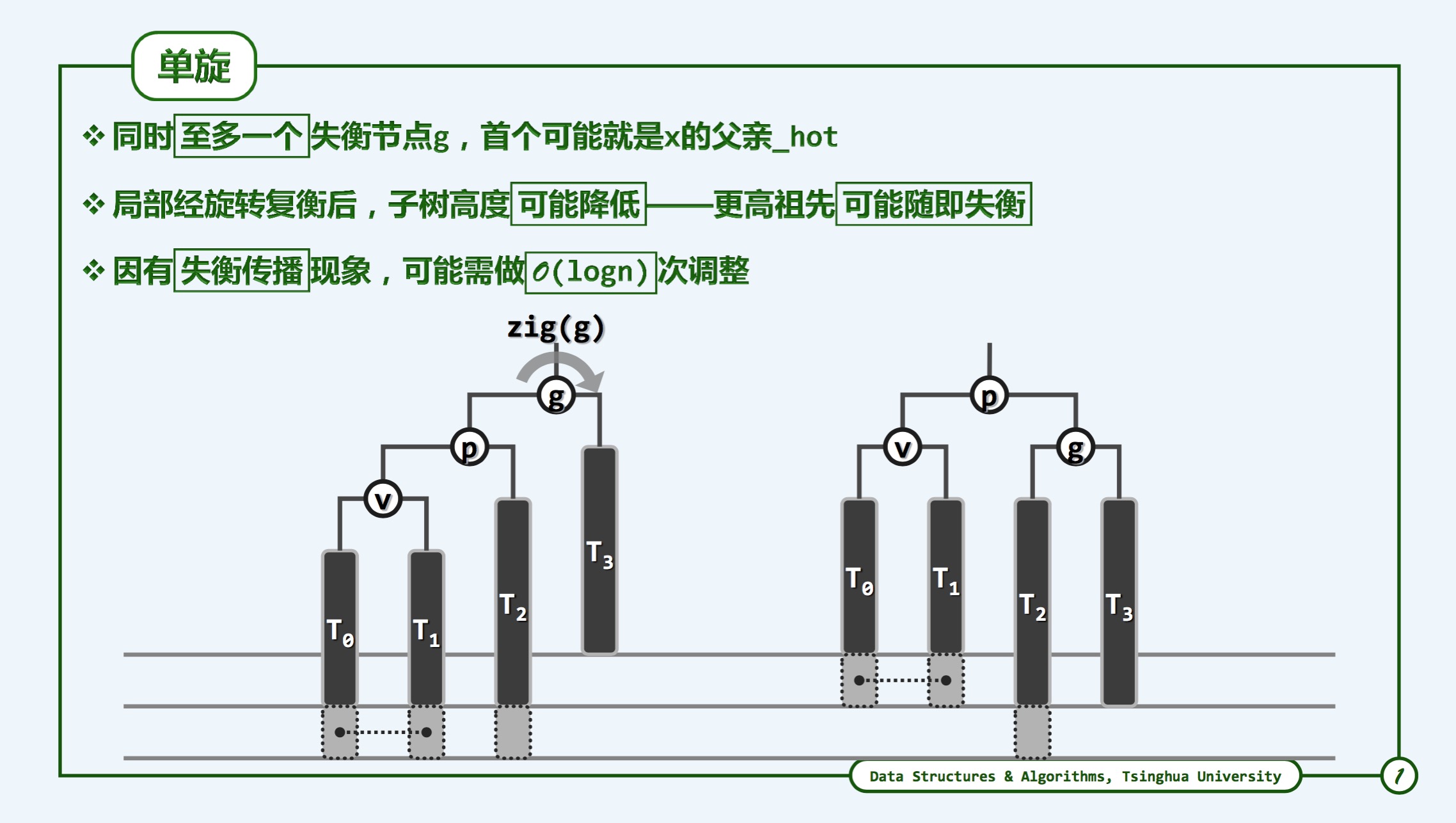
图片转自邓老师pdf,侵权必删
- Q:就图中而言,为什么v的T1, T0俩个后辈一定存在?
- A:如果v下面的俩个后辈不存在,而T2的后辈存在,那么此时T2高度更高,自然选取T2为v
实现代码如下
bool remove(const T &e)
{
/* ----- BST 删除操作(缺少一个高度更新,在AVL中更新) ----- */
BinNodePos(T) x = search(e);
if(!x)
return false; // 删除元素必须保证存在
BST<T>::removeAt(x, _hot);
--_size;
/* ----- AVL 删除所特有的 ----- */
for(BinNodePos(T) g = _hot; g; g = g->parent)
{
if(!AvlBalanced(*g)) // 如果不满足avl平衡条件
{
g = FromParentTo (*g) = rotateAt(tallerChild(tallerChild(g)));
updateHeight(g);
}
}
return true;
}
这里简单回忆下removeAt操作
void removeAt(bnp &x, bnp &hot)
{
bnp w = x;
bnp succ = nullptr;
if(!HasLc(x))
succ = x = x->rc;
if(!HasRc(x))
succ = x = x->lc;
else{
w = w->succ();
swap(x->data, w->data);
bnp u = w->parent;
((u == x) ? u->rc : u->lc) = succ = w->rc;
}
hot = w->parent;
//release(w->data);
if(succ) succ->parent = hot;
delete(w);
return succ;
}
失衡传播:
经过一次删除调整后,原先子树的高度有可能不变,有可能减一。如果发生了减一,那么就相当于从被删除节点
的父亲开始,每次都需要进行AVL平衡条件的检查,一直到树的根部。
树的真正调整
虽然我们已经学习了基本变换,但是我们并不适用,而是仅仅让其帮助我们理解,我们所仍然采用的方式
叫做3+4重构,直接将树的g, p, v拆开,按照a < b < c的方式重新命名,同时其下面的四颗子树也按照
T0 < T1 < T2 < T3 的方式重新命名。最终的状态会达到
T0 < a < T1 < b(root) < T2 < c < T3 的状态
3+4重构在这里非常简洁,所以重点还是这里的rotateAt
template <typename T>
BinNodePos(T)
BST<T>::connect34( // 3+4 重构
BinNodePos(T) a, BinNodePos(T) b, BinNodePos(T) c,
BinNodePos(T) T0, BinNodePos(T) T1, BinNodePos(T) T2, BinNodePos(T) T3)
{
a->lc = T0; if(T0) T0->parent = a;
a->rc = T1; if(T1) T1->parent = a;
updateHeight(a);
c->lc = T2; if(T2) T2->parent = c;
c->rc = T3; if(T3) T3->parent = c;
updateHeight(c);
b->lc = a; a->parent = b;
b->rc = b; c->parent = b;
updateHeight(b);
return b;
}
// 根据我们之前讨论的四种旋转情况,在不同情况下进行a, b, c 以及T0, T1, T2, T3的排序
template <typename T>
BinNodePos(T)
BST<T>::rotateAt(BinNodePos(T) v) // 传入参数为孙子节点v
{
BinNodePos(T) g, p;
p = v->parent;
g = p->parent;
if(IsLChild(*p))
{
if(IsLChild(*v))
{
p->parent = g->parent; // 向上连接
return connect34(v, p, g, v->lc, v->rc, p->rc, g->rc);
}
else{
v->parent = g->parent;
return connect34(p, v, g, p->lc, v->lc, v->rc, g->rc);
}
}
else{
if(IsLChild(*v))
{
v->parent = g->parent;
return connect34(g, v, p, g->lc, v->lc, v->rc, p->rc);
}
else{
p->parent = g->parent;
return connect34(g, p, v, g->lc, p->lc, v->lc, v->rc);
}
}
}
综合评价
AVL树优点:查找,插入,删除均为O(logN)时间复杂度,O(N)的空间
AVL树缺点:
- 需要借助高度或平衡因子,需要改造元素结构,或额外封装,
过于做作 - 实测和理论尚有差距
- 最重要的因子,删除操作后,会经过一次旋转调整,但有可能导致整个局部的树高度比未删除之前减1,因此会再次出发调整,最
坏情况下全树需要做logN次调整, 变化量过于大



 posted on
posted on

